Розберемо шість готових прикладів з геометрії на відстань між точками, прямими і площинами. Завдання взяті із збірника для підготовки до ЗНО тестувань, та будуть корисними в першу чергу учням 10-11 класів. Це і хороша підказка на практичних заняттях з геометрії і добрий безкоштовний репетитор для підготовки до тестування перед вступом у ВУЗ-и. Читайте пояснення та запам'ятовуйте якіі теореми та властивості фігур використані для обчислення завдань.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 35. Прямі та площини в просторі
Задача 35.7 На рисунку зображено куб ABCDA1B1C1D1, ребро якого дорівнює 1.
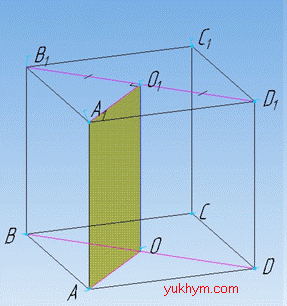
Знайти відстань між прямими AA1 і B1D1.
Розв'язання: Відстань між мимобіжними прямими в просторі – довжина їх спільного перпендикуляра.
За умовою задачі ABCDA1B1C1D1 – куб, кожна грань якого є квадрат.
У квадрата (як ромба) діагоналі перетинаються під прямим кутом.
Звідси слідує, що спільним перпендикуляром для прямих AA1 і B1D1 є відрізок A1O1, де O1 – точка перетину діагоналей грані A1B1C1D1 (що в свою чергу перпендикулярна до прямої AA1).
За умовою задачі, ребро куба ABCDA1B1C1D1 дорівнює 1, тому і сторона квадрата A1B1C1D1 дорівнює 1.
За теоремою Піфагора знайдемо довжину діагоналі A1C1: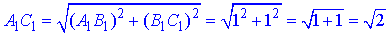 
Оскільки у квадрата (як і у будь-якого паралелограма) діагоналі в точці перетину діляться навпіл, то з цієї умови знаходимо
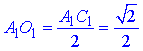– відстань між прямими AA1 і B1D1.
Відповідь: √2/2– Г.
Задача 35.14 Сторона рівностороннього трикутника дорівнює a.
Точка A розміщена від кожної вершини трикутника на відстані b.
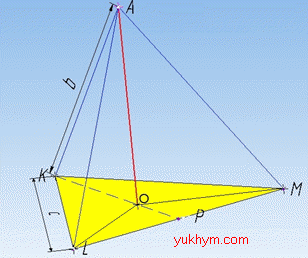
Визначити відстань від точки A до площини трикутника.
Розв'язання: Відстань від точки A до площини трикутника KLM – це перпендикуляр AO опущений з цієї точки на площину (AO⊥(KLM)), основа перпендикуляра (точка O) належить площині KLM.
Оскільки відстань від точки A до кожної вершини ΔKLM однакова і дорівнює b, тобто AK=AL=AM=b (за умовою задачі), то точка O є центром описаного навколо ΔKLM кола з радіусом R (за властивістю: рівні похилі мають рівні проекції):
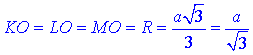
де a – сторона рівностороннього ΔKLM.
Розглянемо трикутник AOK. Оскільки AO⊥(KLM), то AO⊥KO, тому ΔAOK – прямокутний (∠AOK=90), де AK=b – гіпотенуза і KO=a/√3 – катет.
За теоремою Піфагора знайдемо довжину відрізка, катета AO (відстань від точки A до площини трикутника KLM):
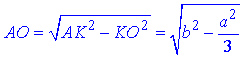
Відповідь: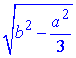 
– Г.
Задача 35.15 Точка M розміщена на відстані m від кожної сторони правильного трикутника і на відстані h від площини трикутника.
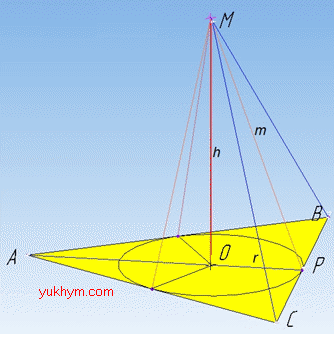
Визначити сторону трикутника.
Розв'язання: Відстань від точки M до сторони трикутника ABC – це перпендикуляр (наприклад, MP) опущений з цієї точки на відповідну сторону BC (MP⊥BC, MP=m за умовою), основа перпендикуляра (точка P) належить стороні BC. Відстань від точки M до площини трикутника ABC – це перпендикуляр MO опущений з цієї точки на площину (MO⊥(ABC)), основа перпендикуляра (точка O) належить площині ABC.
Оскільки відстань від точки A до кожної сторони ΔABC однакова і дорівнює m (за умовою задачі), то точка O є центром вписаного в ΔABC кола з радіусом r (за властивістю: рівні похилі мають рівні проекції):
OP=r.
Розглянемо трикутник MOP. Оскільки MO⊥(ABC), то MO⊥OP, тому ΔMOP – прямокутний (∠MOP=90), де MP=m – гіпотенуза і MO=h – катет.
За теоремою Піфагора знайдемо довжину відрізка, катета OP (радіус вписаного в трикутник ABC кола):
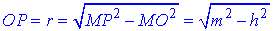
Знайдемо сторону правильного ΔABC за відомим радіусом вписаного кола:
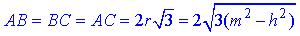
Відповідь: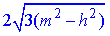 
– В.
Ще три готові приклади на відстані наведені в наступній статті.
