На попередньому уроці проаналізовано готові відповіді до 5 прикладів на кути між прями і площинами в просторі. Далі розберемо 3 готові приклади, які можуть Вас чекати як при проходженні ЗНО тестів, так і на практичних з геометрії.
Задача 35.20 Відрізок завдовжки 10 м перетинає площину, його кінці розміщені на відстані 2 м і 3 м від площини. Знайти кут між даним відрізком і площиною.

Розв'язання: Нехай маємо відрізок BD=10 м, що перетинає площину alpha в точці O.
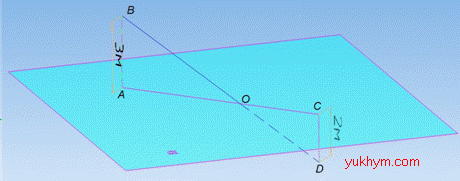
З точки B опустимо перпендикуляр AB=3 м – відстань від точки B до площини alpha, точка A належить площині alpha. З точки D опустимо перпендикуляр CD=2 м – відстань від точки D до площини alpha, точка D належить площині alpha.
Проведемо відрізок AC, який належить площині alpha. Відрізок AC перетинає відрізок BD в точці O (так як через пряму і точку, що не лежить на ній можна провести площину).
В нашому випадку, через пряму AC і точку B можна провести площину (наприклад hamma), в якій міститься пряма BD. Саме в площині hamma прямі AC і BD перетинаються в точці O (на рис. площини hamma немає, це треба уявити, чому саме прямі AC і BD перетинаються в точці O, тут тільки розписано пояснення).
Розглянемо два трикутники AOB і COD. У них AB||CD, оскільки це перпендикуляри опущені з кінців відрізка BD на площину alpha, тому AB⊥AC і CD⊥AC. Звідси маємо:
∠AOB=COD як вертикальні;
∠OAB=∠OCD=90 прямі кути;
∠ABO=CDO як внутрішні різносторонні кути при паралельних прямих AB, CD і січній BD.
Отже, трикутники AOB і COD подібні за трьома кутами. У подібних трикутників відповідні сторони пропорційні. Маємо
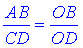
тобто
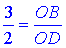
звідси отримаємо OB=3*OD/2.
З іншої сторони,
BD=OB+OD=10 м,
3*OD/2+OD=10,
5/2*OD=10,
отримаємо
OD=4 м і OB=6 м.
Розглянемо прямокутний трикутник AOB (∠OAB=90). Оскільки AB⊥AO і відрізок AO належить площині alpha, то OB=6 м – похила (гіпотенуза ΔAOB), а відрізок AO – проекція похилої на площину alpha. Отже, ∠AOB – кут між відрізком BD і площиною alpha.
За означенням синуса прямокутного трикутника знайдемо ∠AOB, де AB=3 м – протилежний катет до ∠AOB: 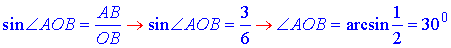
Відповідь: 300 – А.
Задача 35.28 Установити відповідність між відрізками (1–4), побудованими на гранях і ребрах куба, та величинами кутів між ними (А–Д).
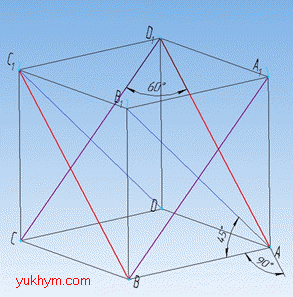
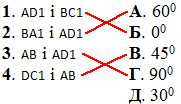
Розв'язання: 1) Оскільки прямі AD і BC лежать в одній площині (ABC1) і не перетинаються, то задані прямі паралельні, тому кут між ними – 00;
1 – Б;
2) Кутом між (мимобіжними) прямими в просторі називають кут між прямими, які перетинаються і паралельні до мимобіжних прямих. Паралельною проекцією прямої BA1 є пряма CD1 (оскільки ABCDA1B1C1D1 – куб, тому його протилежні грані рівні і паралельні).
Звідси, ∠AD1C – кут між прямими BA1 і AD1.
Розглянемо трикутник AD1C. Його сторонами є діагоналі граней куба ABCDA1B1C1D1. У куба всі грані і ребра рівні, тому і діагоналі на його гранях є рівними (за властивістю).
Звідси, випливає, що трикутник AD1C – рівносторонній (у якого всі кути рівні). Тому, за теоремою про суму кутів трикутника
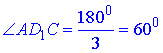
2 – А.
3) Прямі AB і AD1 знаходяться на сусідніх гранях куба, які є перпендикулярними за властивістю куба. Пряма, яка перпендикулярна до площини, перпендикулярна до кожної прямої, що знаходиться в цій площині. В даному випадку пряма AB перпендикулярна до площини ADD, тому AB⊥AD1.
Звідси ∠BAD1=90.
3 – Г.
4) Паралельною проекцією прямої DC1 є пряма AB1.
Звідси, ∠BAB1 – кут між прямими DC1 і AB1.
Розглянемо трикутник BAB1. Його сторонами є ребра BB1 і AB куба ABCDA1B1C1D1. У куба всі грані і ребра рівні, сусідні грані і ребра перпендикулярні, тому ΔBAB1 – прямокутний рівнобедрений (за властивістю), гострі кути якого рівні.
За теоремою про суму кутів трикутника
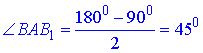
4 – В.
Задача 35.33 З точки B, яка розміщена від площини на відстані 1, проведено дві похилі, які утворюють із площиною кути 450, а між собою – кут 600. Знайти квадрат відстані між кінцями похилих.
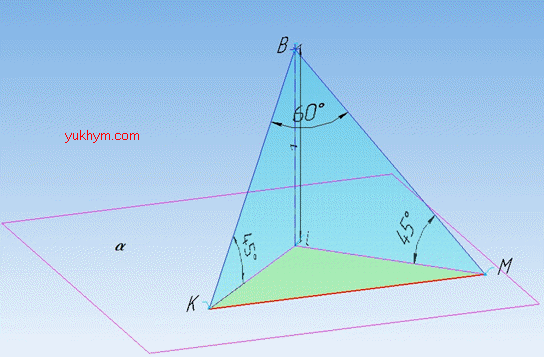
Розв'язання: За умовою задачі маємо площину alpha, точку B, яка не лежить в площині alpha. З точки B опустимо перпендикуляр BL=1 – відстань від точки B до площини alpha (точка L належить площині alpha), тобто BL⊥alpha, тоді BK і BM – похилі, які проведені з точки B до площини alpha, де точки K і M належать площині alpha.
Відрізки KL і ML – проекції похилих BK і BM, відповідно, що належать площині alpha. Оскільки BL⊥alpha, то BL⊥KL і BL⊥ML (пряма, яка перпендикулярна площині, перпендикулярна до кожної прямої, що належать цій площині). Звідси слідує, що ∠BKL=45 і ∠BML=45 – кути між похилими BK, BM, відповідно, і площиною alpha;
∠KBM=60 – кут між похилими BK і BM.
Розглянемо трикутники BKL і BML. Оскільки BL⊥KL і BL⊥ML, то ΔBKL і ΔBML – прямокутні (∠BLK=90 і ∠BLM=90) з відповідно гострими кутами ∠BKL=45, ∠BML=45 і спільним катетом BL=1.
За теоремою про суму кутів трикутника, маємо ∠KBL=45 і ∠MBL=45. Звідси слідує, що ΔBKL і ΔBML – рівнобедрені з основами BK і BM відповідно (кути при основі рівні), тому KL=1 і ML=1 (бічні сторони рівні).
За теоремою Піфагора знайдемо гіпотенузи ΔBKL і ΔBML: 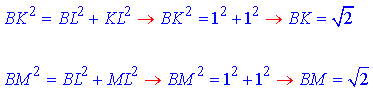
Розглянемо трикутник BKM, у якого ∠KBM=60, BK=√2, BM=√2. Оскільки BK=BM, то ΔBKM – рівнобедрений з основою KM.
За властивістю кути при основі рівні, тому, за теоремою про суму кутів трикутника, маємо
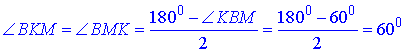
Отримали, ∠KBM=∠BKM=∠BMK=60, звідси (за властивістю) слідує, що ΔBKM – рівносторонній, тому всі його сторони рівні.
Отже, 
Тобто MK2=2 – квадрат відстані між кінцями K і M похилих BK і BM.
Відповідь: 2.
На цьому аналіз готових задач з геометрії не завершується, більше прикладів з суміжних тем наведено в сусідніх публікаціях.


