Готові відповіді до 8 тестових задач на кути між прямими і площинами у просторі допоможуть Вам швидко розібратися з можливими завдання, які Вас чекають як в шкільному курсі геометрії в 10-11 класі так і на початкових курсах у ВУЗ-ах. Завдання охоплюють значну частину теоретичного матеріалу по даній тематиці та будуть корисні великій аудиторії школярів та студентів. Також відповіді можна використовувати при підготовці до ЗНО з математики.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 35.4 Кути між прямими і площинами у просторі
Задача 35.8 Дано куб ABCDA1B1C1D1.
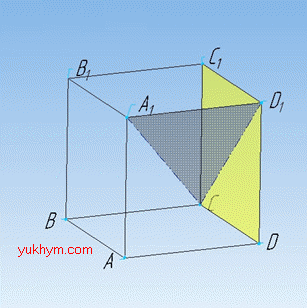
Вказати кут між прямою A1C і площиною DCC1.

Розв'язання: Кутом між площиною і прямою, яка перетинає площину і не є перпендикулярною до площини, називають кут між прямою і її проекцією на площину.
Оскільки проекцією прямої A1C на площину DCC1 (вона ж DD1C1) є відрізок CD1 (дивись задачу 35.5), то кут між прямою A1C і площиною DCC1 є кут A1CD1.
Відповідь: ∠A1CD1 – В.
Задача 35.9 Дано прямокутний паралелепіпед ABCDA1B1C1D1, у якогоABCD – квадрат зі стороною 1, а бічне ребро рівне кореню з трьох AA1=√3.
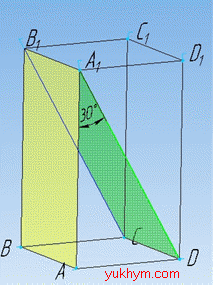
Чому дорівнює кут між площинами AA1B1 і A1B1C?
Розв'язання: Кут між площинами – лінійний кут двогранного кута (про це читайте детально теорію).
Маємо AA1⊥A1B1 і A1D⊥A1B1 (оскільки A1B1CD – прямокутник).
Тому кут між площинами AA1B1 і A1B1C – це кут між ребрами AA1 і A1D, тобто ∠AA1D – лінійний кут двогранного кута.
Знайдемо його величину. Розглянемо трикутник AA1D.
Оскільки ABCDA1B1C1D1 – прямокутний паралелепіпед, то пряма AA1 перпендикулярна до площини ABC, звідси AA1⊥AD, тому ΔAA1D – прямокутний. За умовою задачі:
AA1=√3 – катет, AD=1 – катет.
За означенням тангенса прямокутного трикутника знайдемо кут ∠AA1D:
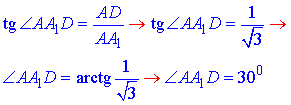
Арктангенс рівний 30 градусам.
Відповідь: 300 – А.
Задача 35.10 Дано куб ABCDA1B1C1D1.
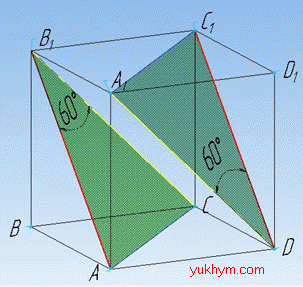
Знайти кут між прямими AB1 і A1D.

Розв'язання: Кутом між (мимобіжними) прямими в просторі називають кут між прямими, які перетинаються і паралельні до мимобіжних прямих.
Паралельною проекцією прямої A1D є пряма B1C (оскільки ABCDA1B1C1D1 – куб, тому його протилежні грані рівні і паралельні).
Звідси, ∠AB1C – кут між прямими AB1 і A1D. Знайдемо його величину.
Аналогічно можна розглянути ∠A1DC1. Розглянемо трикутник AB1C.
Його сторонами є діагоналі граней куба ABCDA1B1C1D1.
У куба всі грані і ребра рівні, тому і діагоналі на його гранях є рівними.
Звідси, випливає, що трикутник AB1C – рівносторонній (у якого всі кути рівні).
Тому, за теоремою про суму кутів трикутника знаходимо шуканий
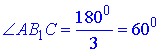
Відповідь: 600 – В.
Задача 35.11 На рисунку ABCD – прямокутна трапеція з прямим кутом B, точка M – середина сторони AD.
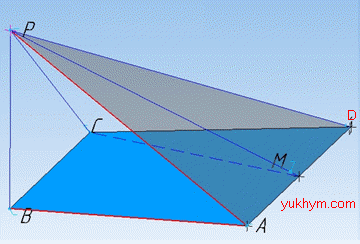
PB – перпендикуляр до площини ABC.
Визначити кут між площинами ABC і APD.
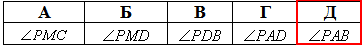
Розв'язання: Кут між площинами – лінійний кут двогранного кута.
Маємо PB⊥AB, оскільки за умовою задачі PB – перпендикуляр до площини ABC
(пряма, яка перпендикулярна до площини, перпендикулярна до кожної прямої, що належить цій площині);
AD⊥AB (оскільки ABCD – прямокутна трапеція з прямим кутом B і AD||BC).
За теоремою про три перпендикуляри маємо PA⊥AD.
Отже, ∠PAB – лінійний кут двогранного кута.
Це і є шуканий кут між площинами ABC і APD.
Відповідь: ∠PAB – Д.
Задача 35.19 Знайти кут між площинами, якщо точка, яка лежить на одній з них, віддалена від прямої перетину площин утричі далі, ніж від другої площини.

Розв'язання: Маємо дві площини alpha і beta, які перетинаються по прямій a.
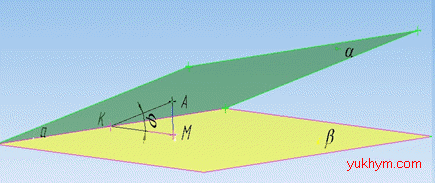
Нехай точка A належить площині alpha. Відстань від точки до прямої перетину – перпендикуляр AK опущений з точки A на пряму a (тобто AK⊥a), де точка K – основа перпендикуляра AK.
Відстань від точки до площини – перпендикуляр AM опущений з точки A на площину beta (тобто AM⊥beta), де точка M – основа перпендикуляра AM, що належить площині beta.
За умовою задачі точка A, що належить площині alpha, віддалена від прямої перетину площин a утричі далі, ніж від площини beta, тобто AK=3*AM.
Проведемо відрізок KM. Оскільки точка K належить прямій a перетину площин, то вона належить площині beta, точка M також належить площині beta.
Звідси слідує, що відрізок KM належить площині beta. Так як AM⊥beta, то AM⊥KM (пряма, яка перпендикулярна до площини, перпендикулярна до кожної прямої, що належить цій площині).
Отже, ∠AKM – лінійний кут двогранного кута, тобто кут між площинами alpha і beta, який треба знайти.
Розглянемо трикутник AKM. Оскільки AM⊥KM, то ΔAKM – прямокутний (∠AMK=90), де AM – протилежний катет до ∠AKM і AK=3*AM – гіпотенуза.
За означенням синуса прямокутного трикутника знайдемо ∠AKM:
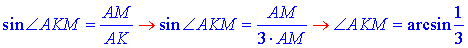
Відповідь: arcsin(1/3) – В.
Три готові задачі, пояснення до яких не вмістилися в даній статті, Ви можете переглянути на наступній сторінці сайту.



