Сьогодні розберемо готові відповіді до задач з геометрії на ортогоналну та паралельну проекцію фігур. Завдання відповідають шкільній програмі навчання, а також можуть бути використані при самостійній підготовці до ЗНО (без репетитора).
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 35.2 Ортогональні і паралельні проекції фігур
Задача 35.4 Яка з наведених фігур не може бути паралельною проекцією прямокутної трапеції? 

Розв'язання: За властивістю паралельного проектування:
1) паралельні прямі переходять у паралельні прямі (або в одну пряму, або в точки);
2) зберігаються відношення відрізків паралельних прямих або однієї прямої.
На основі цих властивостей встановлюємо, що паралелограм не може бути паралельною проекцією прямокутної трапеції.
Відповідь: паралелограм – Д.
Задача 35.5 На рисунку зображено куб ABCDA1B1C1D1. 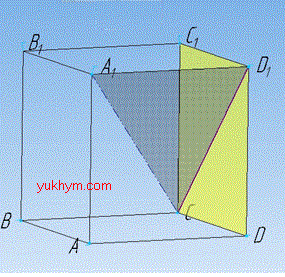
Вказати ортогональну проекцію діагоналі A1C на площину DD1C1.

Розв'язання: Ортогональне проектування – це паралельне проектування прямими, які перпендикулярні площині проекції.
З точки A1 проведемо пряму перпендикулярну площині DD1C1.
Частина цієї прямої буде відрізком A1D1, оскільки, за умовою задачі, ABCDA1B1C1D1 – куб, а у куба (за властивістю) всі ребра перпендикулярні до своїх відповідних граней (площин).
Звідси слідує, що точка A1 проектується в точку D1.
Тому ортогональною проекцією діагоналі A1C є відрізок CD1 (діагональ грані DD1C1).
Відповідь: CD1 – Д.
Задача 35.21 На рисунку зображено куб ABCDA1B1C1D1 з ребром 2a.
Точка M – середина ребра AA1. Встановити вид многокутника, який є перерізом куба площиною MBC, визначити його площу.
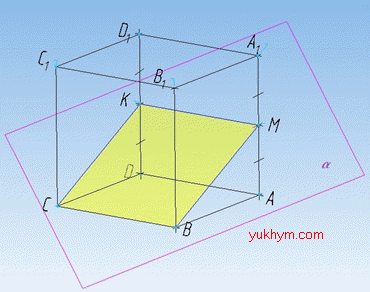
Розв'язання: Маємо куб ABCDA1B1C1D1, який перетнутий площиною alpha. Ця площина проходить через точки M, B і C (за умовою задачі). Оскільки у куба протилежні грані рівні і паралельні, то в перерізі куба площиною alpha отримали чотирикутник MBCK, у якого протилежні сторони паралельні (якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні).
Оскільки протилежні сторони паралельні, то чотирикутник MBCK – паралелограм. У паралелограма протилежні сторони рівні (за властивістю), тому задана площина alpha (або MBC) в точці K ділить ребро DD1 навпіл.
У куба сусідні грані між собою перпендикулярні (за властивістю), тому будь-які прямі проведені у сусідніх гранях куба будуть перпендикулярними, якщо вони перетинаються (або мимобіжними в протилежному випадку). Звідси слідує, що
MB⊥BC, MB⊥MK і KC⊥BC, KC⊥MK.
Чотирикутник MBCK, у якого всі кути прямі – прямокутник, у якого BC=MK=2a, MB=CK.
Розглянемо трикутник AMB. Оскільки ABCDA1B1C1D1 – куб, то AM⊥AB, тому ΔAMB – прямокутний (∠MAB=90), де AB=2a – катет і AM=a – катет.
За теоремою Піфагора знайдемо довжину відрізка, гіпотенузи MB (невідому сторону прямокутника MBCK):
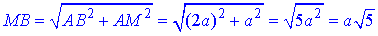
Обчислимо площу прямокутника MBCK (переріз куба площиною MBC):
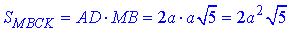
Відповідь: прямокутник, 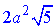 – Г.
– Г.
Задача 35.22 На рисунку зображено правильний тетраедр SABC з ребром a. Точки M, K і P – відповідно середини ребер AS, SC і AB.
Встановити вид многокутника, який є перерізом тетраедра площиною MKP, визначити його периметр.
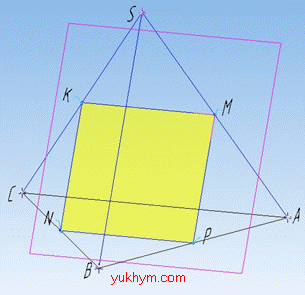
Розв'язання: Маємо правильний тетраедр SABC, який перетнутий площиною MKP. Ця площина проходить через точки M, K і P (за умовою задачі). Оскільки точка P не є вершиною грані SABC, то площини SABC і MKP перетнуться по прямій PN, де N – точка перетину площини MKP з прямою BC і (за властивістю) ділить її навпіл, позаяк точки M, K і P – відповідно середини ребер AS, SC і AB за умовою задачі. (З прямою AC площина MKP не перетинається, інакше б вона співпадала з гранню SAC і точка P б їй не належала, що суперечить умові!).
Отже, в перерізі тетраедра площиною MKP утворився чотирикутник MPNK. Відрізок MK сполучає середини ребер AS і SC, тому за означенням MK – середня лінія трикутника ASC, тому за властивістю, MK||AC і MK=a/2.
Аналогічно встановлюємо, що
MP||BS і MP=a/2;
NP||AC і NP=a/2;
NK||BS і NK=a/2.
У чотирикутника MPNK всі сторони рівні MK=MP=NP=NK=a/2 і протилежні сторони паралельні за властивістю (дві прямі паралельні третій прямій MK||AC і NP||AC, паралельні між собою MK||NP).
Звідси випливає, що чотирикутник MPNK є ромбом. Обчислимо периметр ромба MPNK (переріз тетраедра площиною MKP):
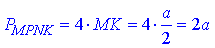
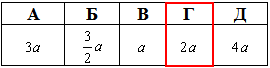
Відповідь: ромб, 2a – Г.



