Завдання на повне дослідження та побудову графіка функції досить поширені як в шкільному курсі так і у ВУЗах при вивченні математичного аналізу.
А все тому, що задавши Вам лише один приклад викладач має можливість визначити Ваш рівень знань, а саме:
знання елементарних функцій;
вміння визначати область визначення та область значень;
знаходити перші та другі похідні функції;
розв'язувати квадратні, трансцендентні рівняння;
знаходити локальні екстремуми та точки перегину на графіку функції;
інтервали опуклості та вгнутості;
і наостанок похилі асимптоти.
Після цього ще потрібно виконати побудову заданої функції, що не для всіх студентів є легким завданням.
Таким чином Ви закріплюєте знання з немалої теми, яку коротко можна назвати "ДОСЛІДЖЕННЯ ФУНКЦІЇ".
Щоб краще оволодіти всіма можливими прийомами необхідно або багато працювати самостійно, або розбирати та аналізувати готові відповіді,
яких Ви можете знайти чимало при сучасному розвитку інтернет технологій.
Тому все що Вам потрібно - це час та бажання вчитися, все решта у Вас є - телефони, ноутбуки, інтернет.
Дослідити функції методами диференціального числення і побудувати їх графіки:
Приклад 1. y=x3+3x2+2x+4
Розв'язання: Алгоритм повного дослідження функції Вам відомий з попередніх публікацій, тож переходимо до аналізу
1) Область визначення функції ОДЗ: xєR, отже 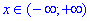
2) Нулі функції: при x=0, y=4.
Графік заданої функції перетинає вісь ординат в точці (0;4).
3) Дослідження на парність:
y(-x)=(-x)3+2(-x)2+2(-x)+4=-x3+2x2-2x+4
функція є ні парною, ні непарною і точно неперіодична.
4) Знайдемо критичні точки функції:
Похідна заданої функції рівна:
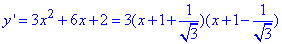
Прирівнюємо похідну до нуля
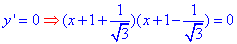
та після розв'язання рівняння визначаємо ординати критичних точок
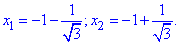
5) Інтервали зростання та спадання, точки max і min функції:
Для зручності записуємо значення точок та поведінку функції в таблицю
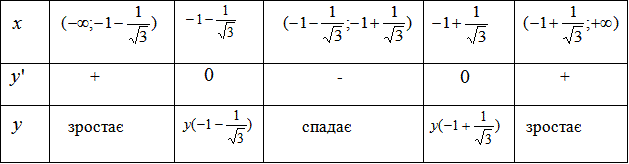
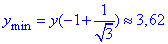 - локальний мінімум функції.
- локальний мінімум функції.
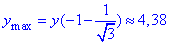 - локальний максимум функції.
- локальний максимум функції.
Точки перегину шукати не будемо, лише нагадаємо, що для цього потрібно шукати другу похідну функцію, прирівняти її до нуля.
З рівності нулю знайти точки підозрілі на перегин та дослідити знак другої похідної справа та зліва.
6) Асимптоти графік заданої функції не має.
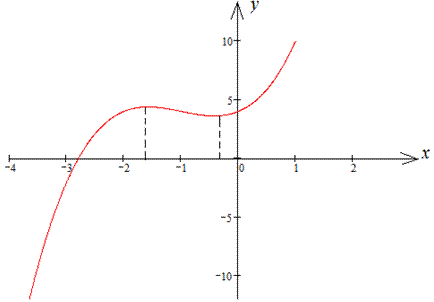
Відповідно до проведеного дослідження виконуємо побудову графіка функції.
В окремих випадках, коли задана складна функція, можете знаходити значення функції в додаткових точках.
Дослідження функції в Мейпл
Наведемо короткий код, який продемонструє наскільки швидко і красиво можна виконати дослідження функції в Мейпл.
Програма собою представляє досить розвинутий математичний пакет для вирішення як студентських задачок, так і завдань з фізики, моделювання, диференціальних рівнянь, статистики і т.д.
Візуалізація коду та відповідей робить Мейпл конкурентом, в порівнянні з аналогічними "солверами".
Спершу занулюємо всі змінні та підключаємо модуль роботи з графіками
> restart; >
with(plots):
Вводимо саму функцію
> y:=x^3+3*x^2+2*x+4;
Знаходимо точку перетину кривою з віссю Ox.
> evalf(solve(y=0,x));
-2,7963219
Evalf служить для округлення до цілих значень, спробуйте забрати його і отримаєте ірраціональні значення коренів кубічного рівняння.
Нас цікавить тільки ціле значення, та як Мейпл видасть Вам ще і два комплексні корені.
Обчислюємо похідну функції
> y1:=diff(y,x);
та з умови рівності похідної знаходимо точки підозрілі на екстремум.
> a:=solve(y1=0,x);
a:=-.4226497307, -1.577350269
Далі визначаємо значення в кожній з точок
> y_1:=subs(x=a[1],y);evalf(y_1);
3,615099821
> y_2:=subs(x=a[2],y); evalf(y_2);
4,384900178
Фрагмент скрішоту коду наведено далі

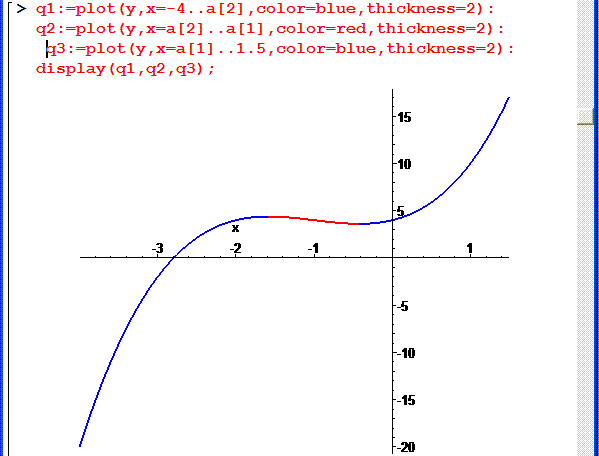
Для повної картини розмальовуємо фрагменти кривої різними кольорами, там де функція зростає – синім, та між точками екстремуму червоним.
> q1:=plot(y,x=-4..a[2],color=blue,thickness=2):
q2:=plot(y,x=a[2]..a[1],color=red,thickness=2):
q3:=plot(y,x=a[1]..1.5,color=blue,thickness=2):
Вкінці виводимо всі три графіки за допомогою функції display.
Якщо перед цим не підключити модуль командою with(plots) то замість виводу сумарного графіку отримаєте повідомлення про помилку.
display(q1,q2,q3);
Параметр thickness -відповідає за товщину ліній на графіку. Якщо не вказувати його, то по замовчуванню товщина кривих рівна одиниці.
Оскільки ми Вам не запропонуємо неробочого коду, то можете поглянути на результат аналізу.
Провести повне дослідження функції та побудувати графік
Приклад 2. y=4x/(x+1)2
Розв'язання: Схему дослідження найкраще вивчати на подібних завданнях, тому запам'ятовуйте що за чим потрібно виконувати.
1) Область визначення функції
ОДЗ: Функція визначена всюди за винятком точки де знаменник перетворюється в нуль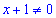 , тому маємо два інтервали
, тому маємо два інтервали 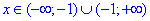
2) Нулі функції: при x=0, y=0.
Графік заданої функції перетинає осі координат в точці (0;0).
3) Дослідження на парність:
Знайдемо вираз ф-ї при від'ємному аргументі
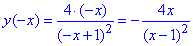
Бачимо, що функція є ні парною, ні непарною.
4) Знайдемо критичні точки функції:
Обчислюємо похідну:
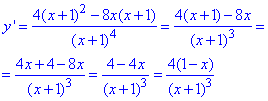
та прирівнюємо її до нуля
y'=0;
1-x=0
, а звідси слідує, що x=1 критична точка.
5) Інтервали зростання та спадання, точки max і min функції заносимо у таблицю:

ymax=y(1)=1- найбільше значення функції.
Д) Асимптоти графіка функції.
Через границю на межы областей визначення знаходимо вертикальну асимптоту:
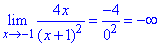
Отже, x=-1 - вертикальна асимптота.
Похила асимптоту знаходимо за формулою y=k*x+b:
Коефіцієнти прямої k,b обчислюємо через відповідні границі функцій
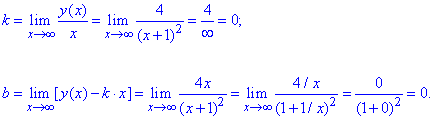
Отже, y=0 - похила асимптота.
Графік функції має вигляд
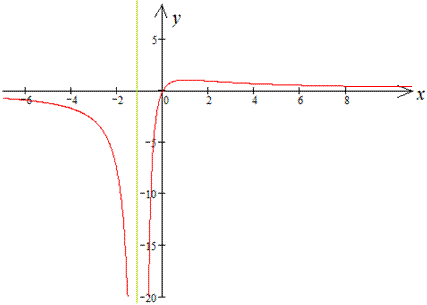
Аналіз функції в Мейпл
Проведемо повторно дослідження заданої фунції в пакеті Мейпл.
Наведемо коментарі лише до частини функцій, що не була прокоментована в першому завданні.
> restart;
> with(plots):
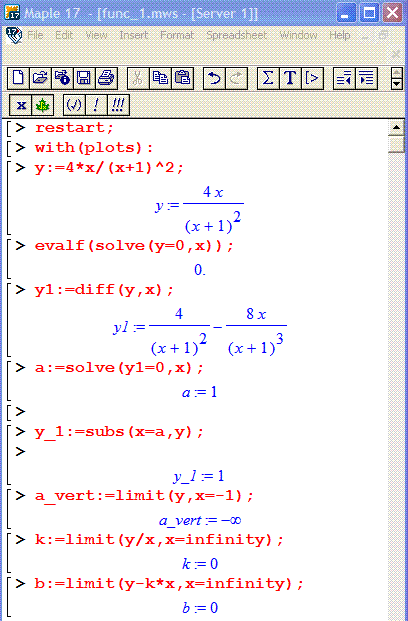
> y:=4*x/(x+1)^2;
> evalf(solve(y=0,x));
Крім того, що Мейпл прекрасно шукає розв'язки рівнянь, обчислення похідних досить гарно організовано з виводом необхідних формул.
> y1:=diff(y,x);
> a:=solve(y1=0,x);
> y_1:=subs(x=a,y);
Також можемо знайти вертикальні та похилі асимптоти за допомогою функції limit.
Для цього після границі слід ввести вираз фінкції, та через "кому" значення до якого прямує аргумент.
infinity - позначення нескінченності.
> a_vert:=limit(y,x=-1);
> k:=limit(y/x,x=infinity);
> b:=limit(y-k*x,x=infinity);
В результаті аналізу функції отримаємо
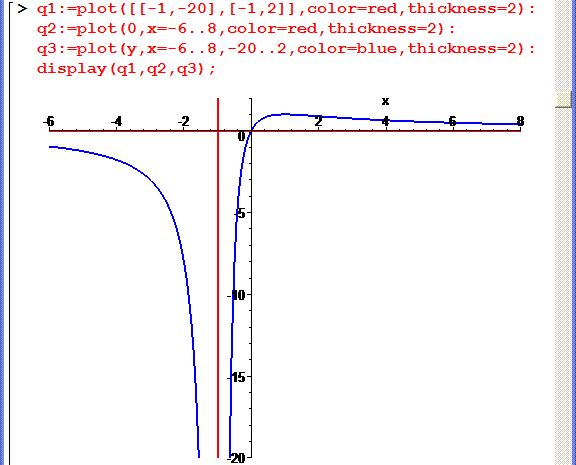
Наостанок будуємо вертикальну асимптоту через дві точки q1, горизонтальну асимптоту q2 та сам графік функції q3.
Його значення по висоті обмежуємо введенням після аргументу x=-6..8 меж -20..2.
> q1:=plot([[-1,-20],[-1,2]],color=red,thickness=2):
q2:=plot(0,x=-6..8,color=red,thickness=2):
q3:=plot(y,x=-6..8,-20..2,color=blue,thickness=2):
display(q1,q2,q3);
Результати розрахунків наведені на графіку.
Саме так як наведено вище може виглядати повне дослідження функцій, якщо поєднувати теоретичні знання паралельно з вивченням математичних пакетів.
Це прискорює аналіз складних тригонометричних, показникових та логарифмічних функцій.
В MathCad та Mathematica всі наведені маніпуляції також доступні, тільки вводити команди потрібно через відповідні вікна.
Мейпл же наближений до програмування, чим і більш цікавий для студентів та викладачів в плані застосування.


