Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики у 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики.
Розділ III. Функції
Завдання 3.1 - 3.45 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.
Завдання 3.26 (Т-06, 26) Знайдіть множину значень функції
f(х)=cos2(х)–sin2(x).

Розв'язання: Задано різницю квадратів тригонометричних функцій. Щоб спростити аналіз додамо та віднімемо синус в квадраті. Функція після спрощень прийме вигляд
f(х) = cos2(х) + sin2(x)–2*sin2(x)=1-2*sin2(x).
Враховуючи, що квадрат синуса приймає значення від 0 до одиниці на всій області визначення знайдемо краї області значень
1-2*0=1; 1-2*1=-1.
Областю значень функції є проміжок [-1;1], який в тестах заданий варіантом А.
Відповідь: А.
Завдання 3.27 (Т-06, 26) Знайдіть множину значень функції
f(х)=(cos(х)+sin(x))2.
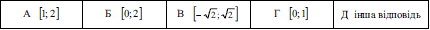
Розв'язання: Спершу підносимо дужку до квадрату та використовуємо формулу для спрощень
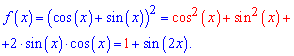
Враховуючи, що синус приймає значення від мінус одиниці до одиниці отримаємо
1-1=0; 1+1=2.
Отже областю визначення функції є проміжок [0;2].
Варіант Б відповідей ідентичний знайденому.
Відповідь: А.
Завдання 3.28 З'ясуйте, для якої із заданих функцій проміжок (0; + безмежність) є її областю значень.
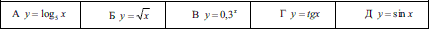
Розв'язання: З наведених функцій тільки коренева має таку область значень. Для самоперевірки можете проаналізувати кожну з наведених у відповідях до тесту функцій.
Відповідь: Б.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Область визначення
- Наступна стаття - ЗНО 2017 математика. Похідна функції в точці


