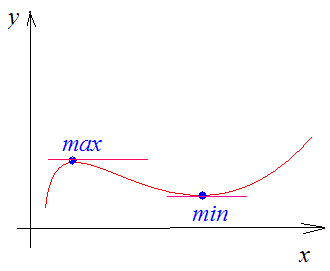
Критичні точки – це точки в яких похідна функції рівна нулю, або не існує. Якщо похідна рівна 0 то функція в цій точці приймає локальний мінімум або максимум. На графіку в таких точках функція має горизонтальну асимптоту, тобто дотична паралельна до осі Ох.
Такі точки ще називають стаціонарними. Якщо бачите на графіку неперервної функції «горб» або «яму» пам'ятайте, що локальний максимум і мінімум досягається в критичній точці. Розглянемо для прикладу наступне завдання.
Приклад 1. Знайти критичні точки функції y=2x^3-3x^2+5 .
Розв'язання. Алгоритм знаходження критичних точок наступний:
- Знаходимо похідну функції
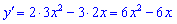
- З умови рівності нулю похідної визначаємо критичні точки функції
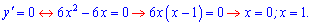
Отже функція має дві критичні точки.
Для повного представлення, який на графіку функції мають вигляд критичні точки побудуємо рисунки в математичному пакеті Мaple:
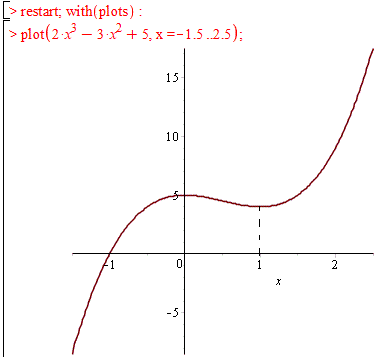
В знайдених точках функція досягає локального максимума та мінімума.
Дослідження функцій на критичні точки, опуклість та вгнутість можна проводити в Мaple, MathCad, MatLab або інших пакетах, але вивчати це будемо на окремих уроках.
Далі, якщо потрібно провести дослідження функції то визначають знак похідної справа та зліва від критичної точки. Якщо похідна при переході через критичну точку змінює знак з «-» на «+», то функція приймає локальний мінімум. Якщо з «+» на «-» маємо локальний максимум.
Другий тип критичних точок це нулі знаменника дробових та ірраціональних функцій
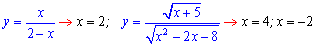
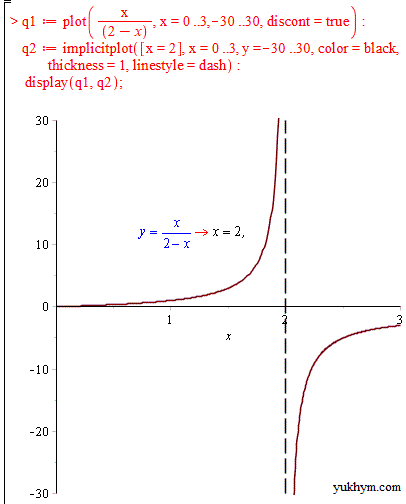
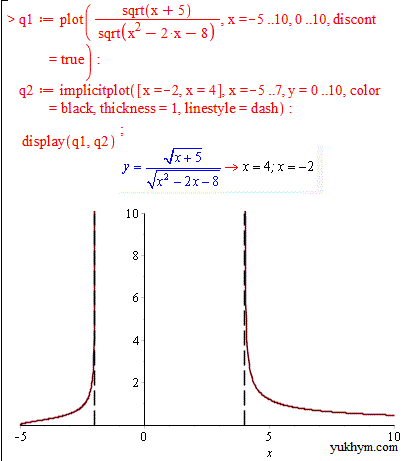
Функції з логарифмами та тригонометричні, які не визначені в цих точках
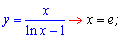
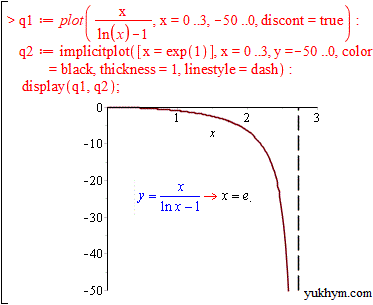
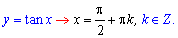
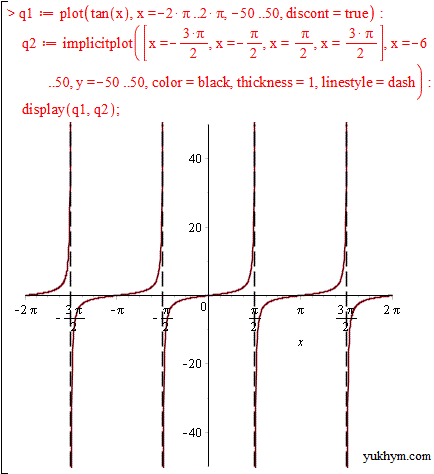
Третій тип критичних точок мають кусково-неперервні функції та модулі.
Для прикладу будь-яка модуль-функція має мінімум або максимум в точці зламу.
Наприклад модуль y=| x -5| в точці x=5 має мінімум (критичну точку).
Похідна в ній не існує, а справа і зліва приймає значення 1 та -1 відповідно.
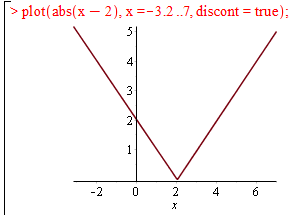
Спробуйте визначити критичні точки наступних функцій.
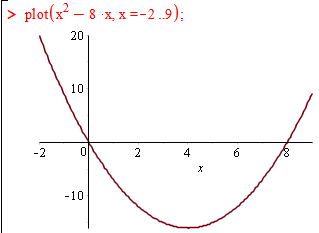
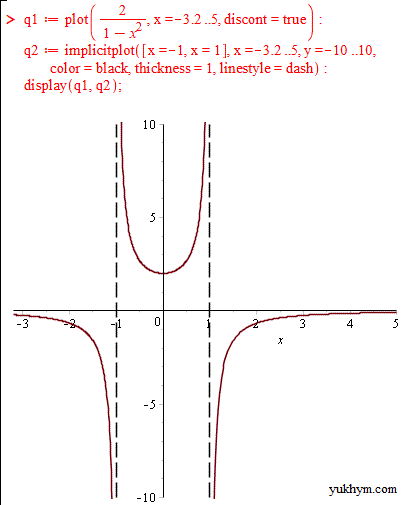
Для повної картини ми побудували графіки функцій з вертикальними асимптотами в Мейплі
1) y=x^2-8x
2) 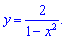
3) 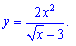
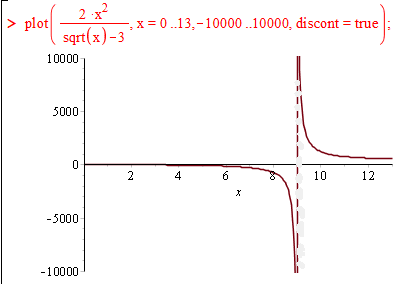
4) 
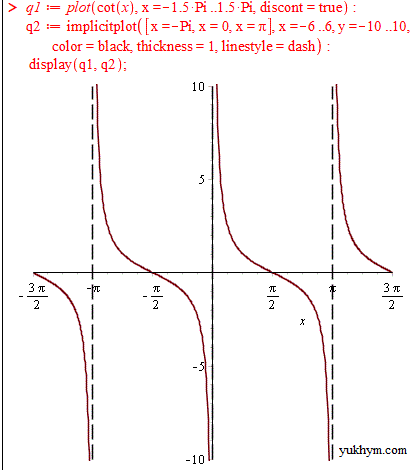
5) 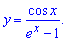
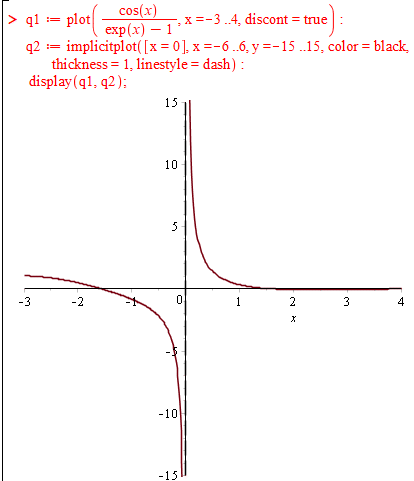
Якщо у відповіді у Ви отримаєте значення
1) x=4;
2) x=-1;x=0; x=1;
3) x=9;
4) x=Pi*k;
5) x=0.
то Ви вже знаєте як знайти критичні точки і зможете справитися з простою контрольною чи тестами.
На графіках функцій їх легко бачити, а от без графків знайти критичні точки допоможе правильне знаходження похідних, тому добре до цього підготуйтеся. В сусідніх публікацях на Вас чекає безліч готових відповідей з дослідження функцій, тому переходіть за посиланнями та вивчайте потрібні Вам розділи математики.