Шановні школярі, випускники, абітурієнти, цей розділ допоможе при підготуватися до зовнішнього оцінювання 2017 року. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці, систематизувати та підвищити накопичений рівень знань з математики. Рішення прикладів з математики будуть цікаві для школярів 9, 10, 11 класів, а так само їх батьків.
Розділ 6. Стереометрія
В завданнях 6.22 - 6.37 правильна відповідь оцінюється 2 балами.
Задача 6.32 Основою піраміди SАВСDЕF є правильний шестикутник АВСDЕF . Грань SАВ - правильний трикутник, площина якого перпендикулярна площині основи. Знайдіть тангенс кута нахилу грані SСВ до основи.
Розв'язання: З умови слідує, що всі грані піраміди нахилені до основи під одним кутом. Оскільки перерізом піраміди є правильний трикутник (всі кути мають 60 градусів), то висота розділяє кут при вершині на 2 по 30 градусів, а кут між ребрами рівнобедреного трикутника і площиною основи рівний
90-30=60 градусів.
В силу симетрії це і є шуканий кут знаходимо тангенс 60 градусів
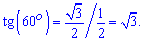
Тангенс нахилу грані до основи рівний корінь з трьох
Задача 6.33 (Т-06, 46) Укажіть номер фужера, у який можна налити найбільше рідини. 1 3 2
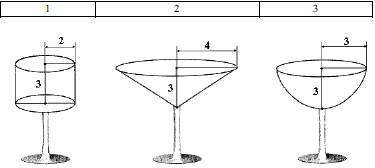
Розв'язання: Знайдемо об'єм тіл, які можна вмістити в фужери. Перше- циліндр з радіусом основи 2 та висотою 3. Об'єм циліндра рівний
V=Pi*2*2*3=12*Pi.
Другий – конус, його об'єм рівний
V=1/3*Pi*4*4*3=16*Pi.
Третій фужер це півсфера радіусом 3.
Об'єм півсфери рівний
V=Pi*3^3/2=13,5*Pi.
Порівнявши об'єми фужерів приходимо до висновок, що у 2 можна налити найбільше рідини.
Задача 6.34 Через вершину конуса з радіусом основи 4 см проведено площину, що перетинає його основу по хорді, яку видно з центра основи конуса під кутом 120°, а з вершини конуса - під кутом 90°. Обчисліть площу перерізу, у см2.
Розв'язання: Завдання настільки надумане, що нам важко уявити, що хотіли від школярів укладачі тестів. Оскільки в тестах відсутній малюнок до завдання то ми не маємо можливості навести хід обчислень. Хто зустрічав дану задачу просьба описати в коментарях або надіслати на пошту.
Задача 6.35 Діагоналі ромба дорівнюють 6 і 8. Куля, яка має радіус 4 дотикається до всіх його сторін. Знайдіть відстань від центра кулі до площини ромба.
Розв'язання: Для обчислення відстані необхідно знати формулу радіуса вписаного у ромб кола
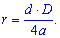
Сторону ромба a знаходимо з прямокутного трикутника, утвореного перетином діагоналей ромба. Його катети рівні 8/2=4 та 6/2=3. Обчислюємо сторону ромба
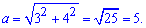
Підставляємо в формулу радіуса кола вписаного у ромб
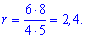
Далі побудуємо переріз сфери площиною, яка проходить через центр сфери а кола. В результаті отримаємо прямокутний трикутник, гіпотенуза якого є радіусом сфери, а радіус кола, що лежить на сфері є одним з катетів трикутника. Другий катет є шуканою відстанню між центром кулі і площиною ромба (центром кола).
Обчислюємо катет прямокутного трикутника
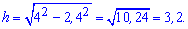
Відстань рівна 3,2.
Допомога з математики у вигляді готових рішень полегшить навчання всіх школярів і буде гарною інструкцією на іспитах і тестах. Готові тестові приклади обов'язково стануть в нагоді у навчанні школярам в 9, 10, 11 класі. Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Площа поверхні, об'єм піраміди
- Наступна стаття - ЗНО 2017 математика. Циліндр, конус, піраміда


