Обчислення скалярного добутку векторів

Геометричне означення: Скалярний добуток  векторів a і b це число, яке рівне добутку модулів (довжин) векторів на косинус кута між векторами:

Алгебраїчне означення: Скалярним добутком двох векторів a і b є скаляр (число), який рівний сумі попарних добутків проекцій векторів на осі.
Дві формули для обчислення скалярного добутку за правилами означень наведені на схемі

Далі на розгляд маємо завдання ЗНО тестів де потрібно знайти скалярний добуток.
Для оптимізації матеріалу ми не ставимо значок вектора зверху над ним, хоча це маємо на увазі. Тому правильним є запис векторів, який фігурує у формулах, Пам'ятайте про це.

Приклад 42.9 Дано вектори a(3;-6;2) і b(8;4;5). Знайти скалярний добуток a•b.

Розв'язування: Скалярний добуток двох векторів a(a_x;a_y;a_z) і b(b_x;b_y;b_z), заданих своїми координатами, обчислюється за формулою:
.
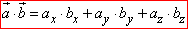Для векторів a(3;-6;2) і b(8;4;5) отримаємо:
a•b=3•8-6•4+2•5=24-24+10=10.
Скалярний добуток більше нуля означає, що кут між заданими векторами гострий, як і показано на рисунку. Якщо кут між векторами тупий, то скалярний добуток завжди менший нуля. Знак має значення, тому Ви повинні знати за що він відповідає вскалярному добутку. Такі питання є на тестах, та й далі піде тема кути між векторами де за допомогою знаку та періодичності косинуса визначають градусну міру кутів між векторами.

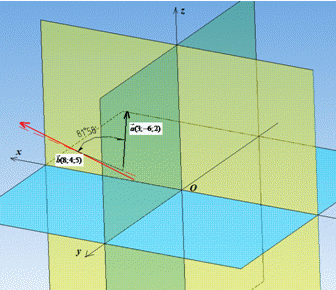
Відповідь: 10 – Г.

Приклад 42.16 Знайти скалярний добуток векторів m і n.

Розв'язування: Випишемо координати початку O і кінця M вектора m:
O(0;0), M(2;3).
Запишемо координати вектора m як різницю координат кінця M(2;3) та початку O(0;0):
M(2-0;3-0)=(2;3).

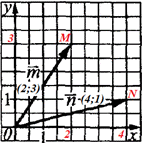
Випишемо координати початку O і кінця N вектора n:
O(0;0), N(4;1).
Запишемо координати вектора n як різницю координат кінця N(4;1) та початку O(0;0):
n(4-0;1-0)=(4;1).
Обчислимо скалярний добуток векторів m(2;3) і n(4;1):
m•n=2•4+3•1=8+3=11.
Відповідь: 11 – В.

Приклад 42.10 Обчислити квадрат довжини вектора a, якщо відомо, що він колінеарний вектору c(2;-2;3) і їх скалярний добуток дорівнює 34.

Розв'язування: Нехай маємо вектор a(x;y;z) і колінеарний до нього вектор c(2;-2;3), тоді за властивістю колінеарності векторів отримаємо:

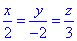
Звідси випливає, що y=-x
(випливає з рівняння x/2=-y/2) і z=1,5x (випливає з рівняння x/2=z/3).
Тому маємо a(x;-x;1,5x).

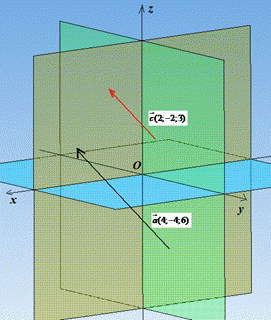
Запишемо скалярний добуток векторів a(x;-x;1,5x) і c(2;-2;3)
(за умовою a•c=34):
Запишемо скалярний добуток векторів a(x;-x;1,5x) і c(2;-2;3) (за умовою a•c=34):

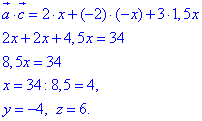
Отримали вектор a(4;-4;6). Знайдемо квадрат його довжини:
.
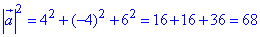Відповідь: 68 – Д.

Приклад 42.12 Сторона рівностороннього трикутника ABC дорівнює 4. Знайти скалярний добуток векторів AB•BC.

Розв'язування: У рівностороннього трикутника ABC всі сторони рівні, тому |AB|=|BC|=4. Також всі кути рівні й дорівнюють 60 градусів (див. рисунок).

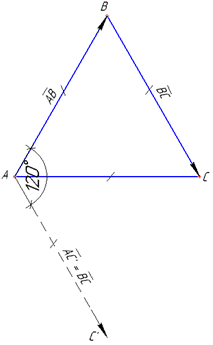
Паралельним перенесенням посунемо вектор BC у точку A, щоб вектори у цій точці мали спільний початок, тоді отримаємо вектор AC', де AC'=BC, тому
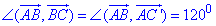- кут між векторами AB і BC (дивись рисунок).
За формулою для обчислення скалярного добутку векторів (через їх довжини та кут між ними) отримаємо:

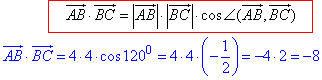
Відповідь: -8 – Б.

Приклад 42.21 Дано вектори a і b такі, що |a|=1, |b|=2, |a+b|=3. Знайти скалярний добуток векторів a і b та кут між ними.

Розв'язування: Такого типу завдання розв'язують методом складання рівняння.
За означенням модуля суми |a+b| і скалярного добутку a•b векторів a і b розв'язуємо

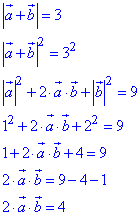
Звідси a•b=2 – скалярний добуток векторів a і b.
Розпишемо тепер a•b через добуток модулів векторів на косинус кута між ними

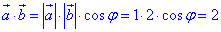
звідси виражаємо cos(φ)=1.
Косинус рівний одиниці, тому робимо висновок, що
φ=0 – кут між векторами a і b.

З рисунку можемо отримати висновок:
якщо кут між векторами рівний нулю φ=0, то |a|+|b|=|a+b|=3.
Відповідь: 2 – Б.

Приклад 42.26 Установити відповідність між векторами (1–4) та їх скалярними добутками (А–Д).

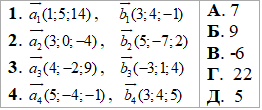
Розв'язування: Скалярний добуток векторів a_n(a₁;a₂;a₃) і b_n(b₁;b₂;b₃) знаходимо за формулою:
.
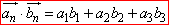Виконуємо обчислення для 4 пар векторів та зіставлення з відповідями для тестів

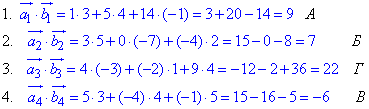
Приклад 42.30 Вектори a і b утворюють кут 120 градусів. Їх модулі рівні |a|=3,|b|=2.

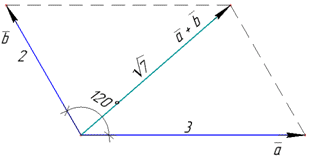
Обчислити:
1) (3a-2b)(a+2b);
2) √7|a+b|.
Розв'язування: Знайдемо скалярний добуток векторів a і b:
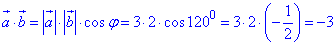, отже отримали a•b=-3,
де φ=120 – кут між векторами a і b, причому

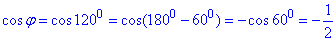
Обчислимо задані вирази, які містять в собі скалярний добуток і довжини заданих векторів a і b:

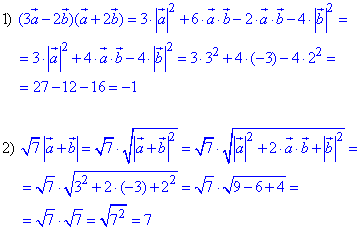
Відповідь: -1; 7.

Приклад 42.32 a(4;-2;-4), b(6;-3;2). Обчислити (2a-3b)(a-2b).
Розв'язування: Знайдемо модуль (довжину) вектора a(4;-2;-4):

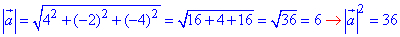
Знайдемо модуль (довжину) вектора b(6;-3;2):

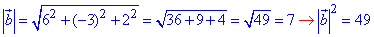
Знайдемо скалярний добуток векторів a і b:

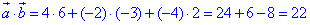
отримали a•b=22.
Обчислимо заданий вираз, який містить в собі скалярний добуток і довжини заданих векторів a і b:

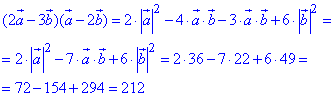
Відповідь: 212.

Приклад 42.29 Відомо, що |x|=3, |y|=6, φ=60, де φ – кут між векторами x і y.

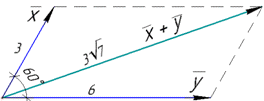
Знайти:
1) x•(x+y);
2) √7|x+y|.
Розв'язування: Знайдемо скалярний добуток векторів x і y:

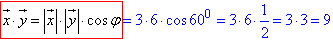
він рівний x•y=9.
Обчислимо задані вирази, які містять в собі скалярний добуток і довжини заданих векторів x і y:
1)
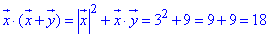
2)
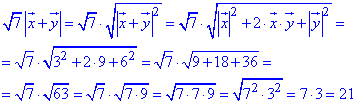
Обчислення не складні, а самі формули легко читати.
Відповідь: 18; 21.

Приклад 42.30 Дано 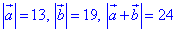. Знайти |a-b|.

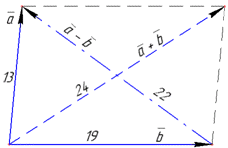
Розв'язування: З означення модуля суми векторів a і b запишемо вираз:

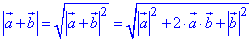
З отриманого рівняння знайдемо значення виразу 2•a•b:

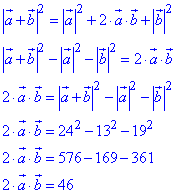
Обчислимо модуль різниці векторів a і b:

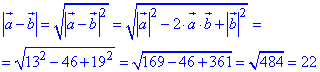
(Для звичайного паралелограма знайти довжину другої діагоналі потрібно за теоремою косинусів, або можна і методом векторів на прикладі цього завдання).
Відповідь: 22.

Приклад 42.43 На озері від пристані одночасно відпливають два катери. Один з них рухається зі швидкістю 25 км/год під кутом 300 до берега, а інший – зі швидкістю 30 км/год перпендикулярно до берега. Якою буде відстань між човнами через 6 хв? Відповідь округлити до сотих кілометра.
Розв'язування: Зробимо математичну модель задачі. Швидкість першого катера позначимо вектором a, тоді його довжина (модуль): |a|=25.
Швидкість другого катера позначимо вектором b, тоді його довжина (модуль): |b|=30.
Напрями векторів a і b зображаємо згідно умовою задачі, як показано на рисунку.

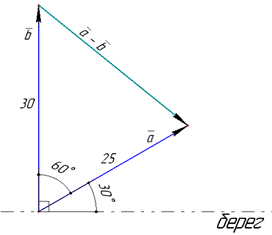
Через деякий час після початку руху катерів швидкість їх буде змінюватися, але вектор швидкості одного катера відносно іншого катера дорівнюватиме різниці векторів обох катерів, тобто a-b, де кут між векторами a і b дорівнює 60⁰ (див. рисунок).
Обчислимо скалярний добуток векторів a і b, де кут між векторами дорівнює 60⁰ (див. рисунок):

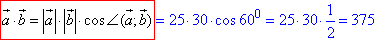
Знайдемо довжину (модуль) вектора a-b:

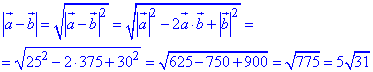
Звідси швидкість одного катера відносно іншого рівна v=5√31 км/год.
Знайдемо відстань s між човнами через 6 хв руху з точністю до сотих кілометра, причому спершу слід перетворити час з хвилин в години
t=6 хв=6/60 год=0,1 год:

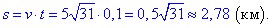
Відповідь: 2,78.

Далі йдуть задачі на умову перпендикулярності та обчислення кута через скалярний добуток.

Вас може зацікавити:
1. Скалярний та векторний добутки. Проекція вектора на вектор
2. Знаходження координат точок, довжин між точками
3. Лінійна залежність і незалежність векторів. Розклад вектора за базисом
4. Скалярний добуток (a,b)
5. Мішаний добуток векторів. Його властивості