Скалярним добутком двох векторів a, b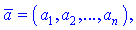 
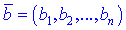називають число, що дорівнює сумі попарних добутків координат векторів з кожної осі, тобто
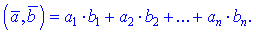
З формули бачимо, що знаходження скалярного добутку – це саме просте заняття, яке може виконати будь-який школяр.
Для прикладу, якщо маємо два вектори в просторі з координатами
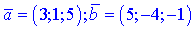
то їх скалярний добуток рівний
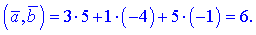
Згідно другого означення, скалярний добуток двох векторів рівний числу, яке отримують множенням довжин векторів (їх модулів) на косинус кута між ними
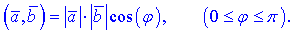
Дане означення використовують не стільки для знаходження скалярного добутку, як значення косинуса кута і вже з таблиць – кута між векторами. З означення отримують зручну формулу для обчислення кута між векторами
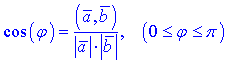
або в координатній формі
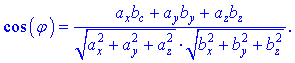
Наведемо приклади обчислення скалярного добутку для тривимірних векторів.
--------------------------------------------
Приклади.
Задано вектори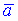 
та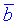 
. Обчислити їх скалярний добуток, якщо
1) 
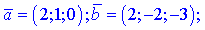
2) 
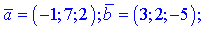
3) 
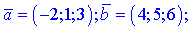
4) 
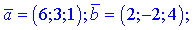
5) 
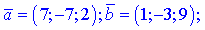
6) 
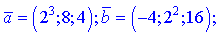
7) 
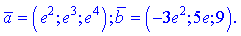
Розв'язання. Виконаємо обчислення згідно першого означення.
1) 
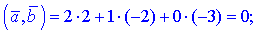
2) 
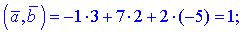
3) 
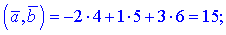
4) 
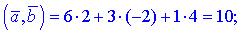
5) 
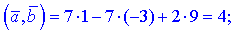
6) 
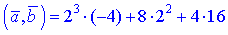
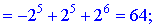
7) 
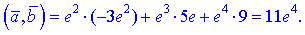
З прикладів, я думаю, Ви переконалися, що знаходження скалярного добутку попарним перемноженням координат векторів, а потім їх сумуванням не є складним. В наступних статтях будуть розглянуті інші сторони скалярного добутку та його застосування до векторного аналізу.
