
В складних числових розрахунках можна зустріти трьох вимірні матриці (у вигляді кубиків) та багатовимірні. Однак Ви їх при здобутті вищої освіти зустрічати точно не будете, тому далі мова піде тільки про знайомі для більшості матриці. Горизонталі елементи матриці називають елементами рядків, вертикальні – відповідно елементами стовпців. В позначеннях розмірності матриці першим йде індекс який вказує кількість рядків, другий кількість стовпців. Наприклад, запис 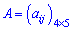 вказує на те, що матриця має 4 рядки і 5 стовпців.
вказує на те, що матриця має 4 рядки і 5 стовпців.
ВИДИ МАТРИЦЬ
В залежності від розмірності та вмісту матриці поділяють на
1) Квадратні 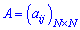 та прямокутні матриці
та прямокутні матриці 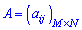 . Наприклад,
. Наприклад,
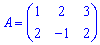 – прямокутна матриця;
– прямокутна матриця;
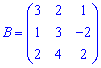 – квадратна матриця.
– квадратна матриця.
2) Одинична матриця – по головній діагоналі одиниці, решта всі елементи рівні нулеві. Позначають великою латинською літерою E.
Для прикладу, матриця
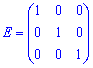 є одиничною матрицею третього порядку.
є одиничною матрицею третього порядку.
3) Діагональна – елементи поза головною діагоналлю нульові, на головній – будь-які. Наприкалад, матриця
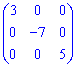
4) Симетрична матриця – елементи такої матриці симетричні відносно головної діагоналі 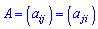 .
.
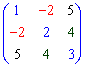
5) Верхня трикутна (нижня трикутна ) матриця – елементи під діагоналлю (над діагоналлю) в таких матрицях нульові. Наприклад,
Верхня трикутна – 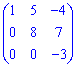
Нижня трикутна 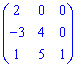
У випадку, коли елементи головної діагональні в трикутній матриці одиничні її називають унітрикутною
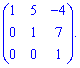
ОПЕРАЦІЇ НАД МАТРИЦЯМИ
Основними операціями над матрицями є додавання, віднімання, множення, транспонування. Щоб легше Вам було зрозуміти правила ми наведемо короткі приклади.
Сумою (різницею) двох матриць називають матрицю, елементи якої утворюються попарним додаванням (відніманням) елементів матриць. Для прикладу, додавання двох матриць
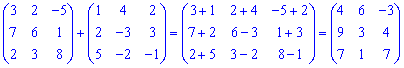
та їх різниця
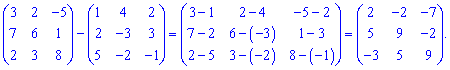
Слід зазначити, що додавати та віднімати можна лише матриці однакових розмірів, тобто кількість рядків першої матриці має дорівнювати кількості рядків другої, те саме стосується і стовпців. Однак кількість рядків і стовпців матриць може не співпадати, тобто сумувати та шукати різниці можна як для квадратних матриць так і для прямокутних.
Транспонуванням матриці називають впорядковану заміну рядків матриці стовпцями і позначають 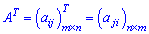 .
.
На практиці транспонування матриці виглядає наступним чином
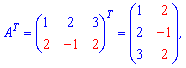
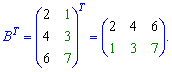
Вибирайте, що Вам візуально зрозуміліше – обидва варіанти дають правильний результат.
Властивості операцій транспонування матриць запишемо в матричному вигляді
1) 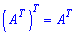
2) 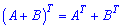
3) 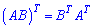
Результатом множення матриці 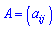 на число
на число  буде матриця
буде матриця  , елементи якої збільшені в
, елементи якої збільшені в  разів порівняно з
разів порівняно з 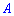 , тобто
, тобто 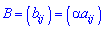 .
.
Множення (добуток) двох матриць 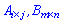 знаходять за правилом, яке можна застосувати лише до матриць в яких кількості стовпців першої та рядків другої матриці співпадають
знаходять за правилом, яке можна застосувати лише до матриць в яких кількості стовпців першої та рядків другої матриці співпадають 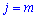 . В результаті отримують матрицю
. В результаті отримують матрицю 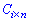 , розмірності кількості рядків першої на стовпців другої з елементами
, розмірності кількості рядків першої на стовпців другої з елементами 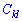 , які рівні сумі попарних добутків елементів
, які рівні сумі попарних добутків елементів 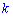 -го рядка першої матриці, на елемент
-го рядка першої матриці, на елемент 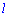 -го стовпця другої матриці.
-го стовпця другої матриці.
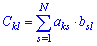
На перший погляд складне і запутане правило досить легко пояснити на практиці. Нехай маємо дві матриці
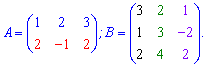
Елементи рядків першої і стовпців другої позначимо в різні кольори для того, щоб Вам наочніше продемонструвати правило множення матриць. Умова рівності кількості стовпців першої матриці = кількості рядків другої виконується (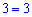 ).
).
Виконуємо обчислення елементів добутку матриць
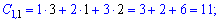
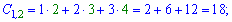
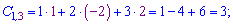
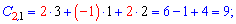
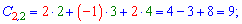
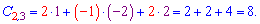
Записуючи матрицю в табличному вигляді
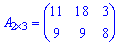
легко переконатися, що утворена матриця має розмірність 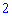 – кількості рядків першої матриці на
– кількості рядків першої матриці на 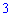 – кількість стовпців другої (про що і було сказано в правилі). За тими ж правилами знаходять добутки квадратних і прямокутних матриць великих розмірів, кількість обчислень при цьому зростає.
– кількість стовпців другої (про що і було сказано в правилі). За тими ж правилами знаходять добутки квадратних і прямокутних матриць великих розмірів, кількість обчислень при цьому зростає.
Додавання та множення матриць можна охарактеризувати властивостями:
1) 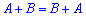 – комутативність
– комутативність
2) 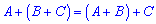 – асоціативність
– асоціативність
3) 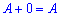
Для будь якої ненульової матриці існує протилежна матриця 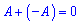
4) Константу можна виносити за правилом 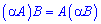
5) Асоціативність множення
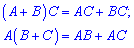
6) 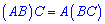
Множення матриць не є комутативною операцією, тобто
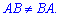
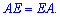
Комутативність має місце лише у випадку коли матриці – квадратні і одна з них є оберненою до іншої, але про це мова піде в наступних статтях. Зараз постарайтеся розібратися з наведеним матеріалом, він стане Вам в нагоді при вивченні складніших операцій з матрицями.
Вас може зацікавити:
]]>
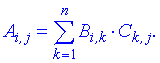 З цього слідує, що перемножити між собою можна матриці в яких кількість стовпців першої B рівна кількості рядків другої C. Нова матриця A, яка є добутком двох, має розмірність m*n, де m – кількість рядків першої матриці, а n – стовпців другої. Правила досить прості, і для знаходження добутку матриць потрібно вміти множити і додавати. Розглянемо кілька прикладів зі збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
З цього слідує, що перемножити між собою можна матриці в яких кількість стовпців першої B рівна кількості рядків другої C. Нова матриця A, яка є добутком двох, має розмірність m*n, де m – кількість рядків першої матриці, а n – стовпців другої. Правила досить прості, і для знаходження добутку матриць потрібно вміти множити і додавати. Розглянемо кілька прикладів зі збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклади. Знайти добуток матриць.
1) (1.110) 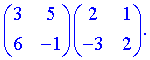
Для знаходження добутку перемножуємо рядки першої матриці на стовпці другої
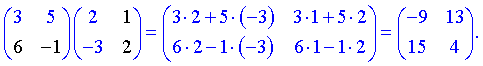
На цьому і побудована операція множення, необхідно почленно перемножити елементи рядка першої матриці на елементи стовпця другої матриці та просумувати. Звідси випливають і властивості добутку матриць, і обмеження на матриці (які можна перемножити, а які ні).
2) (1.112) 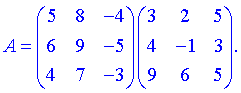
За формулою множення знайдемо елементи нової матриці
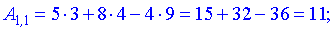
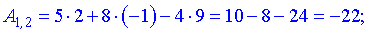
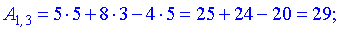
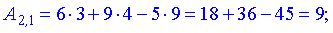
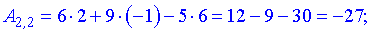
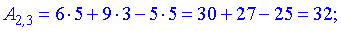
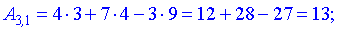
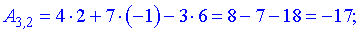
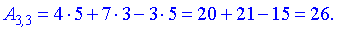
Записуємо отримані значення в матрицю.
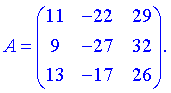
Це і є шуканий резуьтат добутку двох матриць.
3) (1.114) 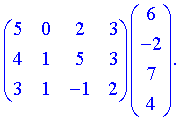
За правилами добутком буде матриця-вектор розмірності 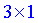 . Обчислимо її елементи
. Обчислимо її елементи
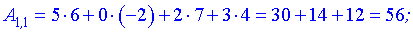
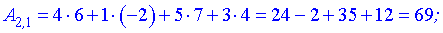
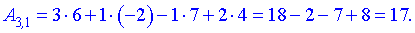
Остаточно матриця набуде вигляду
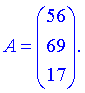
Хоча це біьше усім нагадує вектор, проте це матриця одиничної розмірності.
4) (1.115) 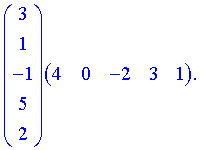
При обчисленні добутку матриць-векторів отримаємо квадратну матрицю розміру 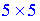 .
.
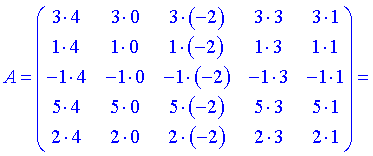
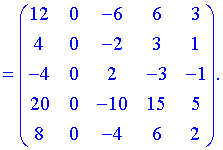
При цьому операцій мінімум, а отримана нова квадратна матриця має п'ятий порядок.
5) (1.116) 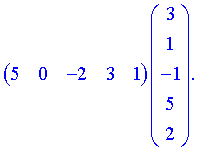
Результатом множення в даному прикладі буде матриця, яка містить лише один елемент.
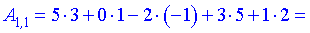
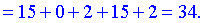
А все тому, що перша матриця має 1 рядок, а друга - один стовпець!
На цьому практична частина уроку завершена. Вправляйтесь в розв'язуванні подібних прикладів, адже множення - це одна з основних операцій (не тільки в матрицях). В наступних статтях матеріал буде складніший, тож починайте знайомитися з матрицями з простого.
Вас може зацікавити:
]]>
Розв'язування багатьох задач математики, економіки, статистики, механіки, зводиться до розв'язування систем лінійних алгебраїчних рівнянь.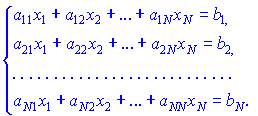 В результаті обчислень отримуємо, що система має один розв'язок, безліч або немає жодного.
В результаті обчислень отримуємо, що система має один розв'язок, безліч або немає жодного.
Давайте вияснимо від чого це залежить?
Розглянемо, для прикладу два лінійних рівняння з двома невідомими:
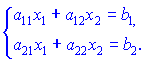
Для розв'язування цих рівнянь ми повинні помножити їх на відповідні множники, при яких виключається одне з невідомих ![]() або
або ![]() : перше на
: перше на ![]() мінус друге на
мінус друге на ![]() для знаходження
для знаходження ![]() ; друге на
; друге на ![]() мінус перше на
мінус перше на ![]() для знаходження
для знаходження ![]()
![]()
![]() На основі цього знаходимо вирази для обчислення коренів системи рівнянь
На основі цього знаходимо вирази для обчислення коренів системи рівнянь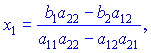
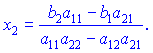 Формули вірні при умові, що знаменник не дорівнює нулю
Формули вірні при умові, що знаменник не дорівнює нулю![]() Якщо знаменник рівний нулю
Якщо знаменник рівний нулю![]() ,то система рівнянь або немає розв'язку, або має нескінченну кількість розв'язків. Вирази в знаменнику (
,то система рівнянь або немає розв'язку, або має нескінченну кількість розв'язків. Вирази в знаменнику (![]() ), які фігурують у двох формулах, називають визначником і позначають
), які фігурують у двох формулах, називають визначником і позначають![]()
Визначником другого порядку називається число, яке дорівнює різниці добутків елементів головної і допоміжної діагоналей, тобто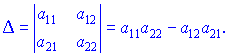 Визначником третього порядку знаходять за правилом трикутників
Визначником третього порядку знаходять за правилом трикутників
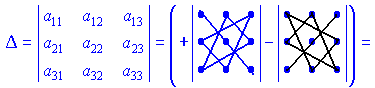
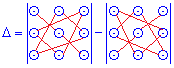
![]() Це правило легко запам'ятати, якщо дописати поряд з визначником перший та другий його стовпці.
Це правило легко запам'ятати, якщо дописати поряд з визначником перший та другий його стовпці.
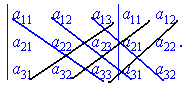
Даний метод обчислення визначника третього порядку називається правилом Саррюса. В процесі обчислень систем лінійних рівнянь встановлено, що визначники рівні сумі доданків, які визначаються як добуток елементів, взятих по одному водночас з кожного рядка і стовпця. Для системи трьох рівнянь в добуток входить три елементи, чотирьох – чотири і т. д. Кількість доданків в визначнику в загальному рівна факторіалу кількості рівнянь. У випадках нульових коефіцієнтів при невідомих знаходження визначника спрощується. Для обчислення визначників старших порядків використовують правила.
ВЛАСТИВОСТІ ВИЗНАЧНИКІВ
1. Величина визначника не зміниться, якщо його рядки замінити стовпчиками, причому кожен рядок замінюють стовпчиком з тим же самим номером (транспонування).
2. Якщо у визначнику поміняти місцями лише два рядки (або два стовпчики), то визначник змінює знак на протилежний, зберігаючи своє абсолютне значення.
3. Якщо визначник має два однакових стовпчики або два однакових рядки, то він рівний нулеві.
4. Якщо визначник містить два пропорційних рядки (стовпчики), то його значення дорівнює нулю. Якщо елементи деякого рядка (стовпчика) дорівнюють нулю, то і сам визначник дорівнює нулю.
5. Якщо всі елементи деякого рядка (стовпчика) помножити на стале число, то значення визначника також помножиться на це число. Звідси слідує, що спільний множник всіх елементів рядка (стовпчика) можна винести за знак визначника.
Як і коли застосовувати основні властивості визначників для спрощення розрахунків Ви знатимете прочитавши наведені в посиланні приклади.
Визначник ![]() -го порядку, за правилом, рівний сумі добутків елементів довільного рядка або стовпця, на відповідні алгебраїчні доповнення. Уявно викреслимо у визначнику
-го порядку, за правилом, рівний сумі добутків елементів довільного рядка або стовпця, на відповідні алгебраїчні доповнення. Уявно викреслимо у визначнику ![]() -го порядку
-го порядку ![]() -й рядок і
-й рядок і ![]() -й стовпець, а з решти елементів утворимо визначник (
-й стовпець, а з решти елементів утворимо визначник (![]() )-го порядку зі збереженням розміщення рядків і стовпців. Отриманий визначник називається мінором визначника і позначається
)-го порядку зі збереженням розміщення рядків і стовпців. Отриманий визначник називається мінором визначника і позначається ![]()
Алгебраїчне доповнення ![]() елемента
елемента ![]() визначника можна подати у вигляді
визначника можна подати у вигляді![]()
Приклад 1 Знайти визначник 4-го порядку
![]()
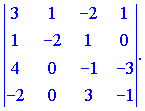
Розв'язок. Розкладемо визначник за елементами другого стовпця
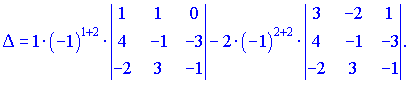
Перший визначник розкладемо за першим рядком
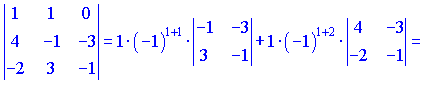
![]()
Другий обчислимо за правилом
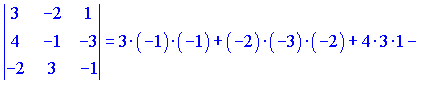
![]()
![]()
Підставляючи в формулу для визначника, отримаємо
![]()
Матричний калькулятор YukhymCALC виконує дані обчилення і виводить результат, швидше ніж Ви зможете ввести відповідні матриці. В результаті отримаємо наступний результат
*** МАТРИЦІ ***
Визначник матриці
Вхідні дані
A=(3;1;-2;1)
(1;-2;1;0)
(4;0;-1;-3)
(-2;0;3;-1)
Det(A)=3*(-2*(-1)*(-1)+1*(-3)*0+0*0*3-(0*(-1)*0+1*0*(-1)+(-2)*(-3)*3))-1*(1*(-1)*(-1)+1*(-3)*(-2)+0*4*3-(0*(-1)*(-2)+1*4*(-1)+1*(-3)*3))-2*(1*0*(-1)+(-2)*(-3)*(-2)+0*4*0-(0*0*(-2)+(-2)*4*(-1)+1*(-3)*0))-1*(1*(-1)*(-1)+1*(-3)*(-2)+0*4*3-(0*(-1)*(-2)+1*4*(-1)+1*(-3)*3))=3*(-2+0+0+0+0-18)-1*(1+6+0+0+4+9)-2*(0-12+0+0-8+0)-1*(0-4+0+0+24+0)= 3*(-20)-1*(20)-2*(-20)-1*20=-60-20+40-20=-60
Завантажте калькулятор і Ви завжди зможете перевірити правильність обчислення визначника 3-4 порядку. Пам'ятайте, що Ви можете помилитися, калькулятор - ні!
Вас може зацікавити:
]]>На питання "Яка матриця має визначник?" можна відповісти коротко і однозначно – квадратна. Не можна знайти визначник прямокутної матриці, таких формул Ви просто не знайдете.
А зараз дамо визначення, що таке визначник та наведемо на прикладах основні його властивості, що на практиці дозволяють спростити їх знаходження. означення
Означення визначника: Визначником (детермінантом) будь-якої квадратної матриці A=(ai,j) називається алгебраїчна сума всіх можливих добутків елементів матриці ai,j, взятих по одному з кожного рядка і стовпця з певним знаком. Цей знак рівний мінус одиниці (-1) в степені кількості інверсій номерів других індексів, коли перші впорядковані в порядку зростання.
Таке правило незручне для сприйняття, тому на практиці користуються простими формулами.
Визначник другого порядку рівний різницю добутків елементів головної та бічної діагоналі:

Визначник третього порядку знаходять за правилом трикутників:
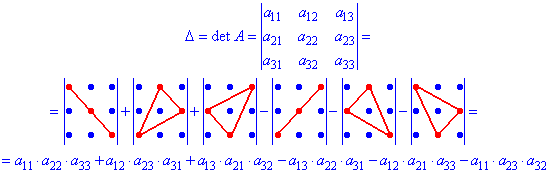
Визначник 3 порядку має 6 доданків з трьох множників у кожному. Формула для визначника четвертого порядку ще складніша і містить 4!=4*3*2=24 доданки, визначник п'ятого порядку утворюється сумуванням 5!=120 доданків, кожен з яких є добутком 5 елементів матриці, взятих відповідно до означення.
Але на практиці визначники 4, 5 порядку теж не обчислюють за загальними формулами, а розкладають через мінори або спрощують, застосовуючи елементарні перетворення над визначниками.
Останні базуються на властивостях визначників, які продемонструємо на прикладах.
Властивості визначників матриць
1. Визначник залишається незмінним при його транспонуванні (тобто заміна рядків на стовпці і навпаки не змінює результуюче значення).
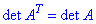
Доведення продемонструємо на прикладі визначника 2 порядку
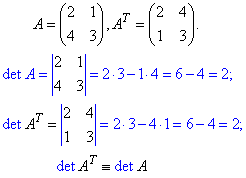
2. Якщо всі елементи деякого рядка чи стовпця визначника дорівнюють нулю, то і сам визначник дорівнює нулю.
Це доведемо без наведення прикладів – справа в тому, що кожен доданок у визначнику має елементи з кожного рядка і стовпця. Звідси слідує, що у кожній сумі буде множник рівний нулю, і відповідно сам визначник теж.
3. Якщо у визначнику замінити місцями два сусідні рядки чи стовпці, то визначник змінить знак на протилежний. Важливим тут є слово сусідні, оскільки якщо змінити 1 і 2 рядки то матимемо –det(A), якщо 1 і 3 то знак зміниться двічі, а два рази –(–) рівний (+), матимемо det(A).
4. Значення визначника залишиться тим самим, якщо до будь-якого рядка (стовпця) додати інший, помножений на довільне число або лінійну комбінацію інших рядків.
Суть цього правила в тому, що всередині визначника можна виконувати певні маніпуляції, але при цьому не можна нічого робити з рядком чи стовпцем над яким робимо ці перетворення.
Для прикладу, нехай маємо матрицю 3 порядку з наступними елементами
A(1, 2,3; 4,5,7;3,3;1).
Якщо знайти детермінант матриці A за правилом трикутника, то він рівний det(A)=9.
Але при цьому буде чимало обчислень, тому спробуємо занулити частину елементів.
Для цього від друго рядка віднімемо перший, і в отриманій матриці від третього рядка віднімемо другий.
В результаті елементарних дій матриця перетвориться до наступної
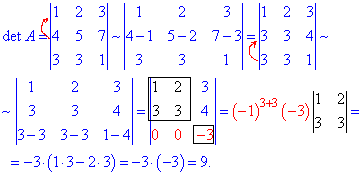
Тут наприкінці було використано розклад визначника через алгебраїчні доповнення до 3 рядка.
Оскільки два елементи =0, то лише третій вносить вклад.
Отже маємо det(A)=9, що рівно значенню за правилом трикутників.
А тепер порівняйте скільки операцій множення та сумування потрачено при кожному з варіантів і Ви зрозумієте, що часто другий метод є швидший і в нього менша статистика допущення помилок при розрахунках. При знаходженні визначниів четвертого та вищіх порядків даний метод показує кращу ефективність ніж, для матриць 2, 3 порядку.
З цієї властивості випливають наступні.
5. Визначник у якого рівні два однакові рядки чи стовпці дорівнює нулеві.
Як доведення можна сказати, що над одним з рядків (стовпців) визначника можна виконати перетворення описані в попередньому пункті. Таким чином один рядок (стовпець) матиме нульові елементи, що за 2 властивістю веде до det(A)=0.
Наприклад
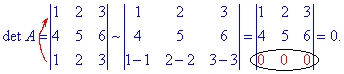
6. Спільний множник можна винести з рядка чи стовпця визначника і записати його перед визначником.
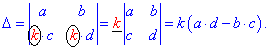
Правило використовують, коли при елементарних перетвореннях слід змінювати рядок (стовпець), який модифікуємо. Тоді при домноженні на можник (k), він автоматично йде в заменник дробу перед визначником. Інше застосування полягає в зменшенні трудоємкості обчислень при великих значеннях елементів матриці. Для прикладу
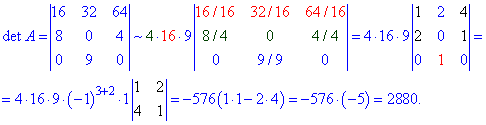
Тут правило винесення спіьного множника до рядка використано тричі + застосовано розклад визначника через алгебраїчні доповнення до третього рядка, що вилилося в обчислення одного мінору 2 порядку.
Таким чином знайшли визначник і він рівний det(A)=2880.
А тепер прикиньте, скільки потрібно обчислень, якщо не використовувати калькулятор, щоб отримати таке значення.
Інше трактування правила - якщо деякий рядок чи стовпець детермінанта помножити на довільне число (k) , то значення визначника зміниться у (k) разів.
7. Сума попарних добутків елементів деякого рядка чи стовпця на відповідні алгебраїчні доповнення до іншого рядка чи стовпця визначника рівна нулеві.

Властивість доводити не будемо, оскільки на практиці Ви цю властивість навряд чи застосуєте.
8. Якщо елементи будь-якого рядка (стовпця) визначника записати у вигляді суми, то цей визначник можна подати у вигляді суми відповідних визначників.
Наприкад
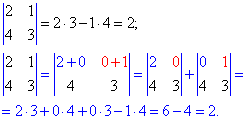
З цієї формули вивести наступну формулу.
9. Розклад визначника через елементи рядка чи стовпця
Визначник рівний сумі добутків елементів будь-якого рядка (стовпця) на алгебраїчні доповнення до таких елементів.
Для матриці 3 порядку розклад визначника за 2 рядком матиме вигляд
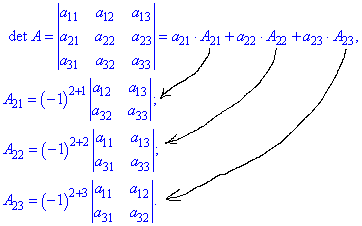
Ця властивість є архіважливою при розписанні визначників 4, 5 порядку через алгебраїчні доповнення, що дозволяє понизити на одиницю порядок шуканих визначників. Так, замість одного визначника 4 порядку, потрібно знайти 4 визначники четвертого порядку.
Таких прикладів мало, однак без знання формул розкладу важко знайти кінцеве значення.
Також, як частковий випадок наведемо ще дві корисних властивості.
10. Для верхньої трикутної чи нижньої трикутної матриці визначник рівний добутку діагональних елементів.
Доведення не потребує, оскільки просто перевірити із загальних формул.
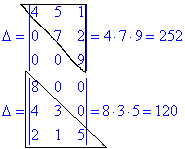
11. Подібне до попереднього, тільки стосується бокової діагоналі. Якщо у визначнику елементи над (під) боковою діагоналлю рівні нулю то він рівний добутку елементів діагоналі, взятим зі знаком «мінус».
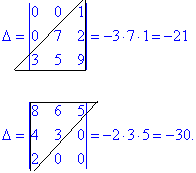
Останні два правила корисні, оскільки на практиці часто зустрічаються розріджені чи блочні матриці, які через елементарні перетворення рядків чи стовпців не важко звести до трикутного вигляду. Всі подальші обчисення зводяться до множення діагональних елементів.
Вчіть правила та вдало застосовуйте на практиці!
Вас може зацікавити:
]]>Про все це ви дізнаєтеся, дочитавши дану статтю до кінця, і якщо вмієте обчислювати визначники, то з прикладами на мінори та алгебраїчні доповнення труднощів у Вас не буде. Для початку основні означення, щоб всі хто знайомиться з темою знали про що йде мова.
Мінором M[j,k] визначника є визначник, одержаний з даного викреслюванням рядка та стовпця, які стоять на перетині до елемента a[j,k].
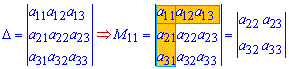
Мінори є визначниками на одиницю меншого порядку ніж матриця для якої їх шукають.
Визначник n порядку має кількість n* n мінорів (рівно кількості елементів матриці).
Для матриці 2*2 мінорами будуть протилежні елементи по діагоналі
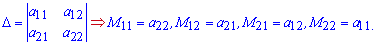
Алгебраїчне доповнення А[j,k] – це мінор M[j,k], взятий зі знаком "плюс" , якщо j+k – парне число і зі знаком "мінус" – якщо непарне
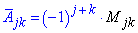
Матриця алгебраїчнихбдоповнень - це матрия складена з визначників А[j,k],j,k=1..n.
Знаки мінорів спрощено можна подати у вигляді схем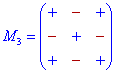
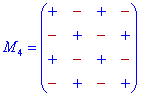
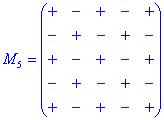 Визначник будь-якого порядку n, згідно правила Лапласа, можна записати у вигляді суми по парних добутків елементів рядків (стовпців) на їх алгебраїчні доповнення.
Визначник будь-якого порядку n, згідно правила Лапласа, можна записати у вигляді суми по парних добутків елементів рядків (стовпців) на їх алгебраїчні доповнення.
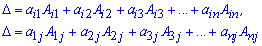
Алгебраїчне доповнення А[j,k], як і мінор, це визначник на одиницю меншого порядку ніж головний визначник. Тому для обчислення визначника n порядку потрібно обчислити n визначників n-1 порядку.
На практиці визначники матриць через алгебраїчні доповнення розписують до тих пір, поки не отримають мінори 3 порядку, які знаходять за правилом Саррюса або трикутників.
Практична реалізація для матриць більших 4 порядку складна, але реалізація таких алгоритмів на мові програмування через рекурентні формули значно спрощує обчислення.
В навчанні переважно оперують з матрицями максимум 4,5 порядку. Якщо маємо розріджені матриці (багато елементів нульових) то визначник за рядком (стовпцем), який містить найбільшу кількість нульових елементів k зводиться до знаходження кількох (n-k) визначників на 1 меншого порядку від основного. Тому з допомогою елементарних перетворень спочатку перетворюють визначник, щоб отримати найбільше нульових елементів, а вже потім розписують його через алгебраїчні доповнення. Щоб Вас не навантажувати зайвою теорією перейдемо до практичної реалізації.
Приклад 1. Знайти мінори матриці 2*2
1)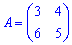
Розв'язок. Матриця мінорів за правилами матиме вигляд
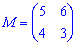
2)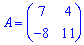
Розв'язок. Міняємо місцями елементи та записуємо у матрицю мінорів
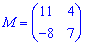
Приклад 2. Знайти мінори матриці 3*3
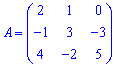
Розв'язок. Викреслюємо перший рядок і стовпець для отримання мінора до першого елемента матриці
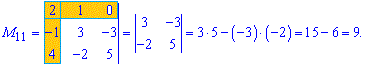
За такою схемою знаходимо усі мінори
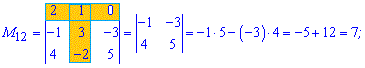
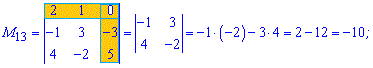
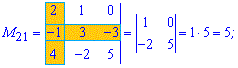
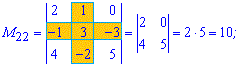
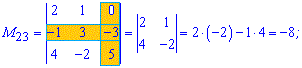
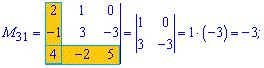
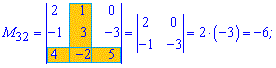
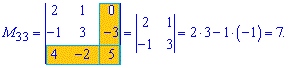
Отримані значення записуємо в матрицю мінорів
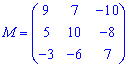
Думаю, після таких детальних пояснень Ви точно зможете знайти мінори самостійно.
Приклад 3. Знайти алгебраїчні доповнення матриці 3*3
1) 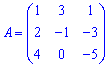
Розв'язок. За наведеною вгорі схемою обчислюємо алгебраїчні доповнення, для цього знаходимо мінори з відповідними знаками
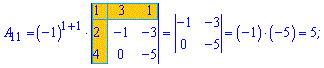
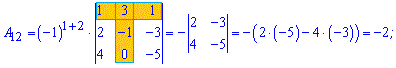
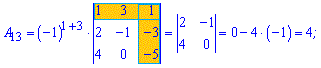
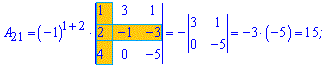
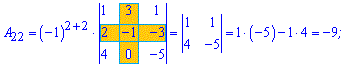
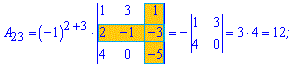
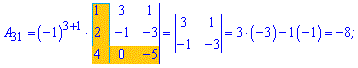
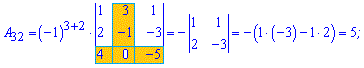
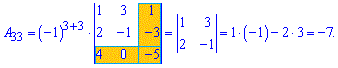
Думаю, що тепер Ви точно знаєте як знайти алгебраїчні доповнення.
Знайдені алгебраїчні доповнення записуємо у вигляді матриці
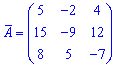
Також, для простоти обчислень, можете спочатку обчислювати мінори, а далі записувати їх у матрицю алгебраїчних доповнень з відповідними знаками. Вибирайте для себе зрозуміліший і простіший спосіб.
Приклад 4. Знайти визначник матриці 3*3
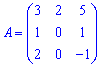
Розв'язок. Знайдемо визначник за правилом трикутника
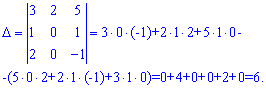
Як бачите багато добутків рівні нулю, оскільки присутні елементи. Тепер, для порівняння, за правилом Лапласа розкладемо визначник через алгебраїчні доповнення другого стовпця
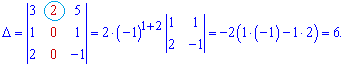
Легко переконатися, що обчислень менше, тільки потрібен час та практика, щоб звикнути до такої схеми обчислень.
Приклад 5. Знайти визначник матриці 4*4
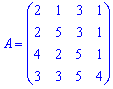
Розв'язок. На перший погляд нас чекає обчислення чотирьох мінорів третього порядку. Але насправді дану кількість можна спростити! Уважно погляньте на перший і другий рядок – вони відрізняються одним елементом. Виконаємо над визначником 4 порядку елементарне перетворення, а саме, від другого рядка віднімемо перший.
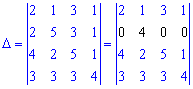
Знак визначника при цьому не поміняється. Тепер розкладемо визначник за елементами 2 рядка. Ми отримаємо 1 доданок у розкладі
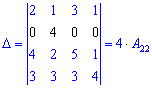
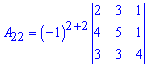
Обчислення вже спростилися. Давайте далі від другого рядка віднімемо перший щоб зробити нулем одиницю
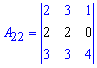
або від третього віднімемо перший, щоб позбутися 3.
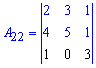
Тоді мінор 3 порядку можна, як визначник, розписати через алгебраїчні доповнення до другого або третього рядка. Обчислимо останній визначник
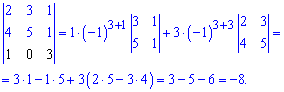
Підставимо знайдене значення у головний визначник
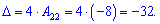
Таким чином завдяки правилу Лапласа та елементарним перетворенням нам вдалося звести відшукання визначника 4 порядку до обчислення 2 визначників 2 порядку. На практиці такі дії економлять багато часу, а в умовах контрольної чи тесту це має вирішальне значення. Тому добре розберіть наведені формули обчислень визначників та алгебраїчних доповнень та застосовуйте їх на практиці.
Вас може зацікавити:
]]>Схеми знаків при мінорах для детермінантів 3-го – 5-го порядку наведено нижче.
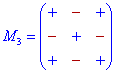
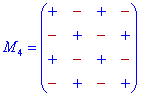
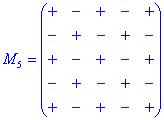
Їх не важко запам'ятати, якщо знати наступні правила:
1. Доповнення до елементів головної діагоналі йдуть зі знаком «+», а на паралельних діагоналях чергуються «-», «+», «-», ...
2. Доповнення до елементів непарних стовпців та рядків починаються зі знаку «+», а далі чергуються «-», «+», для парних починаються зі знаку «-», а далі почергово змінюються «+», «-»,...
Другим правилом користується більшість студентів, оскільки воно прив'язане до стовпця чи рядка за яким здійснюється розклад визначника.
Перейдемо до розгляду прикладів розкладу детермінантів та вивчення особливостей цього методу.
Приклад 1. Розкласти визначник третього порядку за елементами першого рядка та другого стовпця
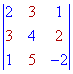
Розв'язання. Проводимо розклад за елементами першого рядка
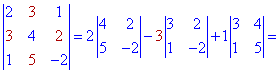
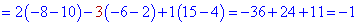
Подібним чином виконуємо обчислення розкладу за елементами другого стовпця
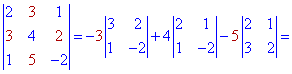
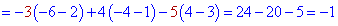
Обидва значення однакові, а значить розрахунки проведені правильно. Якщо у Вас вийде, що визначники отримані розкладом по рядку і стовпцю не співпадають – значить десь допущена помилка і потрібно перерахувати або знайти її.
Приклад 2. Знайти визначник четвертого порядку методом розкладу
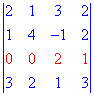
Розв'язання. Розкладемо визначник матриці за елементами третього рядка (виділений червоним), та як в ньому найбільше нульових елементів.
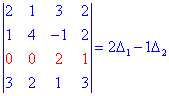
Визначники, що входять в розклад знаходимо за правилом трикутників
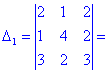
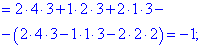
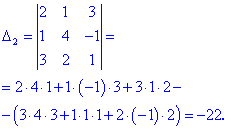
Знайдені значення підставляємо та сумуємо
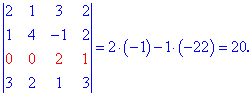
На цьому прикладі метод розкладу показав свою ефективність та простоту. Стандартні правила виявилися б надто громіздкими в обчисленнях.
Приклад 3. Знайти визначник п'ятого порядку методом розкладу

Розв'язання. Як і впопередньому завданні, шукаємо рядок чи стовпець, що містить максимальну кількість нульових елементів. Проводимо розпис визначника
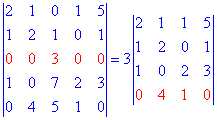
Отриманий визначник розкладемо за четвертим рядком
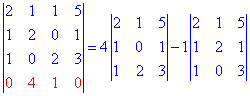
та обчислюємо його складові
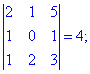
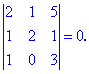
Підставляємо в вихідний детермінант та спрощуємо
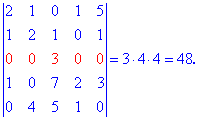
Метод розкладу визначника за елементами рядків чи стовпців є найшвидшим при обчисленні визначників великих розмірів. Замість громіздких та складних обчислень, в яких висока вірогідність допустити помилку, відшукання визначника зводиться до великої кількості простих операцій, які під силу кожному.
Вас може зацікавити:
]]> Визначники позначають наступними знаками det(A), |A|, delta
Визначники позначають наступними знаками det(A), |A|, delta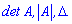 Далі наведені приклади обчислення визначників.
Далі наведені приклади обчислення визначників.
Приклад 1. Знайти визначник матриці
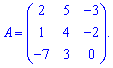 Розв'язання: Застосовуємо правило трикутника для знаходження визначника
Розв'язання: Застосовуємо правило трикутника для знаходження визначника
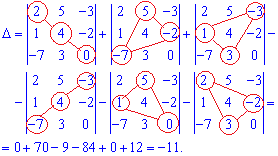
Визначник рівний 11.
Наведена схема стане Вам в нагоді для обчислення визначника матриці 3*3. Все що Вам потрібно – підставити свої значення
Приклад 2. Обчислити визначник матриці
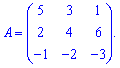 Розв'язання: З метою навчити Вас чогось нового, знайдемо визначник матриці за правилом Саррюса.
Розв'язання: З метою навчити Вас чогось нового, знайдемо визначник матриці за правилом Саррюса. Схема обчислень приведена вище, тому копіювати її не будемо, а лише розпишемо в деталях. Для цього дописуємо до стандартного визначника два перші стовпці і виконуємо наступні розрахунки .
Схема обчислень приведена вище, тому копіювати її не будемо, а лише розпишемо в деталях. Для цього дописуємо до стандартного визначника два перші стовпці і виконуємо наступні розрахунки .
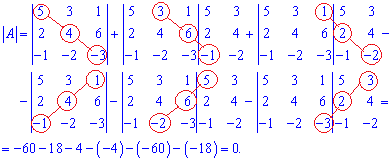
Обчислення не сладні, і тут допустити помилку набагато складніше ніж в правилі трикутника. Там Ви можете помилитися з розміщенням трикутника, зі знаком, а в правилі Саррюса все набагато спрощено.
Приклад 3. Знайти визначник матриці 3*3
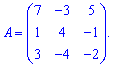 Розв'язання: Застосовуємо правило трикутника для знаходження визначника
Розв'язання: Застосовуємо правило трикутника для знаходження визначника
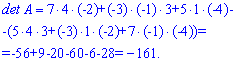
Детермінант рівний -161.
Приклад 4. Обчислити визначник матриці
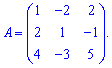 Розв'язання: Знаходимо визначник матриці 3*3 за правилом трикутників
Розв'язання: Знаходимо визначник матриці 3*3 за правилом трикутників
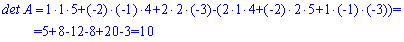
В результаті отримаємо десятку.
Приклад 5. Знайти визначник матриці
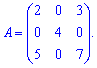 Розв'язання: Матриця має декілька нульових елементів. Такі матриці ще називають розрідженими. Для зменшення кількості операцій обчислимо визначник через алгебраїчні доповнення до другого рядка або стовпця .
Розв'язання: Матриця має декілька нульових елементів. Такі матриці ще називають розрідженими. Для зменшення кількості операцій обчислимо визначник через алгебраїчні доповнення до другого рядка або стовпця .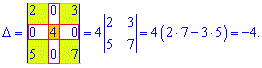
Простіше вже не може бути. Це набагато зручніше, ніж виписувати 6 добутків, чотири з ких дадуть нуль.
Приклад 6. Довести, що визначник матриці А рівний 3.
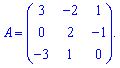 Розв'язання: Матриця містить два нульових елементи, тому можемо знайти визначник через алгебраїчні доповнення. Розкладемо визначник за елементами першого стовпця.
Розв'язання: Матриця містить два нульових елементи, тому можемо знайти визначник через алгебраїчні доповнення. Розкладемо визначник за елементами першого стовпця.
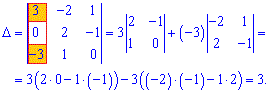
Визначник рівний 3, що і треба було доказати.
Приклад 7. Знайти визначник матриці
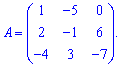 Розв'язання: Детермінант матриці обчислюємо через алгебраїчні доповнення першого рядка або третього стовпця. Виконуємо розрахунки
Розв'язання: Детермінант матриці обчислюємо через алгебраїчні доповнення першого рядка або третього стовпця. Виконуємо розрахунки
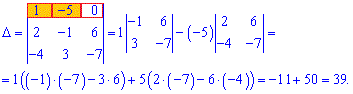
Визначник рівний 39.
Приклад 8. При яких значеннях параметра а визначник матриці рівний нулеві
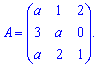 Розв'язання: Завдання з параметром - це вже новий рівень обчислень, тому вивчайте схему.
Розв'язання: Завдання з параметром - це вже новий рівень обчислень, тому вивчайте схему.
За правилом трикутників знаходимо визначник
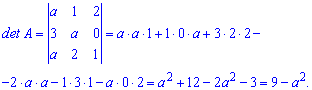
За умовою прирівнюємо визначник до нуля та знаходимо параметр
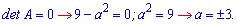
Є два параметри при яких визначник перетворюється в нуль a=-3;a=3.
Приклад 9. Знайти визначник матриці
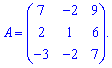 Розв'язання: Обчислимо визначник матриці за правилом трикутників та через алгебраїчні доповнення. За першою схемою отримаємо
Розв'язання: Обчислимо визначник матриці за правилом трикутників та через алгебраїчні доповнення. За першою схемою отримаємо
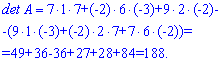
Тепер розкладемо за допомогою алгебраїчних доповнень, наприклад, за третім стовпцем. Він зручний тим, що містить найбільші елементи матриці. Знаходимо визначник
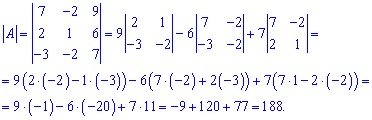
Порівнянням кількості розрахунків переконуємося, що в таких випадках доцільніше використовувати правило трикутників. Обчислення простіші і менша ймовірність зробити помилку.
Для розріджених матриць чи більшого порядку блочних вартує застосовувати розклад визначника за рядком чи стовпцем.
І наостанок бонус від нас – матричний калькулятор YukhymCalc.
 З його допомогою Ви легко перевірите правильність виконання основних операцій з матрицями, а також зможете знайти визначник матриці та обернену матрицю. Для матриць 3*3 використовується правило трикутників, для 4*4 – розклад визначника через елементи першого рядка. Меню досить просте та інтуїтивно зрозуміле не ті.
З його допомогою Ви легко перевірите правильність виконання основних операцій з матрицями, а також зможете знайти визначник матриці та обернену матрицю. Для матриць 3*3 використовується правило трикутників, для 4*4 – розклад визначника через елементи першого рядка. Меню досить просте та інтуїтивно зрозуміле не ті.
Визначник 7 завдання через матричний калькулятор матиме наступний виглядьки студенту, а й школяру.
Перевага матричного калькулятора перед іншими, зокрема онлайн –калькуляторами, в тому, що Ви бачите всі проміжні операції. А це важливо для перевірки та контролю помилок.

Використовуйте наведені схеми обчислень визначників у навчанні. Якщо виникають труднощі в обчисленнях та є можливість, то можете перевірити знайдені визначники калькулятором. Завантажити матричний калькулятор YukhymCalc Ви можете без реєстрації за цим посиланням.
Вас може зацікавити:
]]>Приклад 1. За правилом трикутника знайти визначники матриць
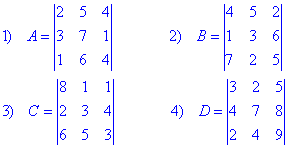
За формулою трикутників виконуємо обчислення визначників
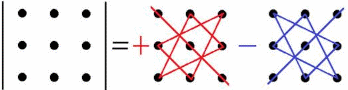
Почленно сумуємо добутки трьох елементів матриці за наведеною схемою. Її потрібно вивчити та .
1) Det(A)=2•7•4+5•1•1+4•3•6-(4•7•1+5•3•4+2•1•6)=56+5+72-28-60-12=33.
2) Det(B)=4•3•5+5•6•7+2•1•2-(2•3•7+5•1•5+4•6•2)=60+210+4-42-25-48=159.
3) Det(C)=8•3•3+1•4•6+1•2•5-(1•3•6+1•2•3+8•4•5)=72+24+10-18-6-160=-78.
4) Det(D)=3•7•9+2•8•2+5•4•4-(5•7•2+2•4•9+3•8•4)=189+32+80-70-72-96=63.
Приклад 2. Методом розкладу за рядком чи стовпцем знайти визначник матриці. Порівняти з результатом, отриманим за правилом трикутників. 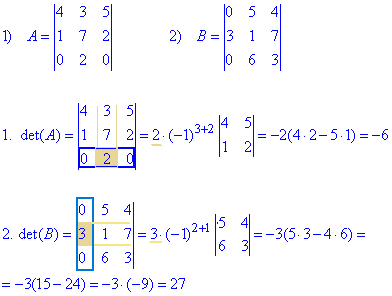
В першому прикладі другий елемент в третьому рядку=2 є ненульовим, тому розкладали визначник за 3 рядком. Нульові складові не враховували, а лише ті, що вносять вклад.
Другий визначник розкладемо за першим рядком, шукаємо мінор і помножуємо на (-1) в степені сум номера рядка та стовпця для ненульового елемента.
Далі знаходимо детермінант за відомою схемою трикутників.
Det(A)=4•7•0+3•2•0+5•1•2-(5•7•0+3•1•0+4•2•2)=0+0+10+0+0-16=-6.
Det(B)=0•1•3+5•7•0+4•3•6-(4•1•0+5•3•3+0•7•6)=0+0+72+0-45+0=27.
Як можна порівняти, багато добутків рівні нулю внаслідок двох нульових елементів, тому не дають вкладу.
Хоча їх доводиться записувати. Перший алгоритм швидший, але вимагає уваги при виписуванні визначника другого порядку та підрахунку степені j+k для множника (-1).
Приклад 3. Довести, що визначник матриці рівний нулю
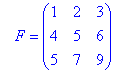
Бачимо, що усі елементи матриці ненульові, тому визначник третього порядку знаходимо за правилом трикутника
Δ=1•5•9+2•6•5+3•4•7-(3•5•5+2•4•9+1•6•7)=45+60+84-75-72-42=0.
Det(F)=0, що і потрібно було довести.
Приклад 4. Обчислити визначник матриці
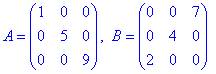
Задано дві діагональні матриці, в першій елементи головної діагоналі ненульові, в другої матриця ненульова бокова діагональ. Якщо не розкладати детермінант за елементами рядка чи стовпця, а пригадати правило трикутників, то при добутку елементів головної діагоналі стоїть знак «плюс», а при добутку елементів бокової діагоналі стоїть знак «мінус».
Тому визначники діагональних матриць рівні:
Δ1=1•5•9=45;
Δ2=-2•4•7=56.
Для перевірки вірності кінцевих відповідей обчисліть наведені визначники самостійно.
Приклад 5. Чому рівний визначник матриці
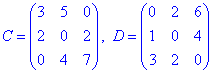
Перша матриця на боковій діагоналі має нульові елементи, всі решта ненульові.
В другої матриці на головній діагоналі всі елементи рівні нулю.
Обчислимо визначник матриці двома способами:
перший – за правилом трикутників,
другий – розкладом за рядком чи стовпцем.
Перший визначник рівний сумі добутку трьох елементів симетричних боковій діагоналі, тому входять зі знаком мінус.
Другий – рівний сумі добутку елементів навколо головної діагоналі, тому стоять зі знаком «плюс».
Це напряму слідує з правила трикутників.
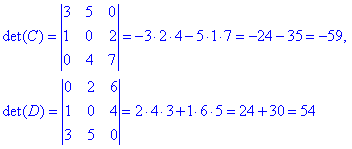
Далі обчислимо ці ж детермінанти шляхом розкладу першого Δ за елементами третього стовпця, другого Δ за елементами другого рядка. 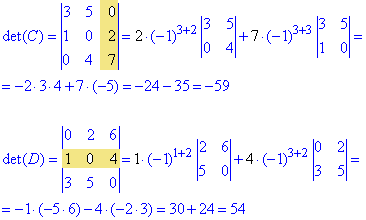
Щоб розібратися з останніми формулами почитайте правила розкриття визначників за елементами рядків та стовпців.
Далі Вас чекають нові завдання на визначники та обернені матриці. Переходьте та вивчайте алгоритми розрахунків.
За довідник візьмемо збірник задач Дубовика В.П., Юрика І.І. "Вища математика ". Пізніше будуть додані приклади обчислення визначника матриці з інших джерел.
Приклади. Обчислити визачник матриці
1) (1.4) 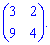
Застосуємо правило обчислення визначника для матриці другого порядку.
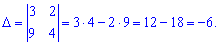
2) (1.6) 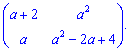
Знаходимо визначник другого порядку перехресним множенням
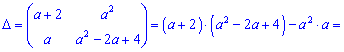
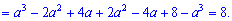
3) (1.8) 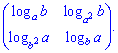
Даний приклад виглядає складним, бо містить логарифми, проте зі знанням наступних правил
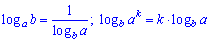
розв'язується напрочуд швидко.
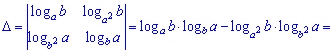
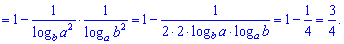
4) (1.14) 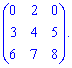
Обчислимо даний визначник двома способами: правилом трикутників та через алгебраїчні доповнення.
За формулою трикутників отримаємо
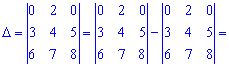
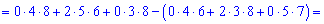
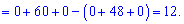
А зараз розкладемо за елементами першого рядка, оскільки в ньому найбільше нулів
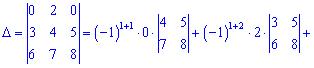
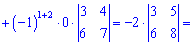
В цьому прикладі спеціально виписані доповнення біля нульових множників, оскільки не всі розуміють звідки беруться доповнення. За правилом вони рівні визначнику, який утворюється викреслюванням рядка 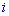 та стовпця
та стовпця 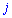 того елемента
того елемента 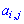 , для якого шукаються, помноженому на мінус одиницю в степені суми індексів
, для якого шукаються, помноженому на мінус одиницю в степені суми індексів 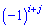 .
.
Схематично на прикладі матриці четвертого порядку це виглядає так:
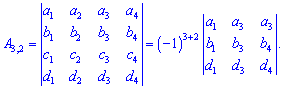
Уважно подивіться, які елементи у визначнику виписані для доповнень і Вам все стане зрозуміло.
Суть методу алгебраїчних доповнень полягає в тому, що коли ми маємо матрицю з нульовими елементами то, розклавши її за за рядком чи стовпцем в якому найбільше нулів нам залишається обчислити стільки визначників на порядок менших від основної матриці, скільки є ненульових елементів. Це значно спрощує обчислення.
6) (1.19) 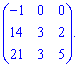
Якщо обчислення проводити за правилом трикутників, то отримаємо багато нульових добутків. В такого роду прикладах доцільно використовувати алгебраїчні доповнення.
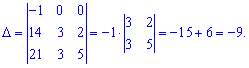
Ось для чого і потрібно використовувати властивості визначників - для спрощення обчислень.
7) (1.21) 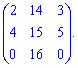
Обчислимо визначник через алгебраїчні доповнення третього рядка. Він вигідний тим, що містить два нульові елементи матриці
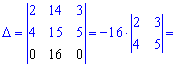
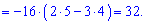
Як можна переконатися, розв'язок з допомогою алгебраїчних доповнень у випадках розріджених матриць можна отримати швидко і без великої кількості обчислень.
8) (1.58) 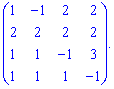
Виконаємо елементарні перетворення - від другого рядка віднімемо перший, а від четвертого – третій. Отримаємо розріджену матрицю
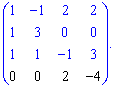
При цьому знак не помняється, бо ми не змінювали рядки місцями. Визначник знайдемо через алгебраїчні доповнення до четвертого рядка
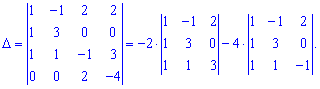
Обчислимо кожен з доданків
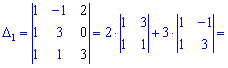
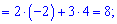
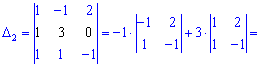
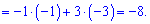
Підставляємо у визначник та сумуємо
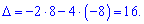
Ось так швидко порахували детермінант 4 порядку.
9) (1.72) 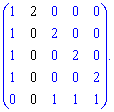
Знайдемо визначник через розклад за рядками і стовпцями, що містять нулі (виділені чорним).
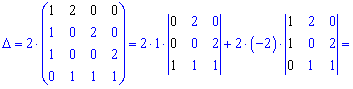
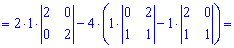
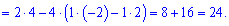
Таким методом знаходження визначника п'ятого порядку звелося до простих обчислень. Практикуйте та вчіть правила і через деякий час у Вас виходитиме не гірше. До зустрічі в наступних уроках!
Вас може зацікавити:
]]>Метод розкладу за елементами рядків або стовпців
Перший приклад ми розглянемо з детальними поясненнями усіх проміжних дій.
Приклад 1. Обчислити визначник матриці 4х4 методом розкладу.

Розв'язання. Для спрощення обчислень розкладемо визначник четвертого порядку за елементами першого рядка (містить нульовий елемент). Вони утворюються множенням елементів на відповідні їм доповнення (утворюються викреслення рядків та стовпців на перетині елемента, для якого обчислюються - виділено червоним)
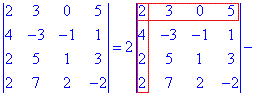
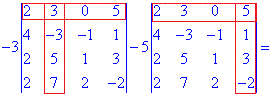
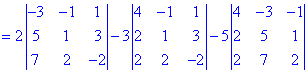
В результаті обчислення зведуться до відшукання трьох визначників третього порядку. Їх знаходимо за правилом трикутників
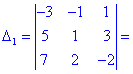
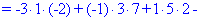
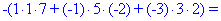
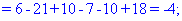
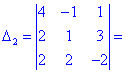
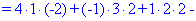
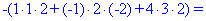
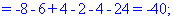
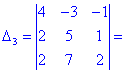
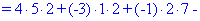
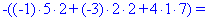
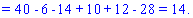
Знайдені значення підставляємо в вихідний детермінант
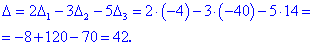
Результат легко перевірити за допомогою матричного калькулятора YukhymCALC . Для цього вибираємо пункт Матриці-Визначник матриці, розмір матриці вводимо 4*4.
Записуємо саму матрицю та здійснюємо обчислення. Результатом розрахунків буде наступний вивід даних
 Результати співпадають, отже обчислення проведені вірно.
Результати співпадають, отже обчислення проведені вірно.
Приклад 2. Обчислити визначник матриці четвертого порядку.

Розв'язання. Як і в попередньому завданні виконуємо обчислення методом розкладу. Для цього виберемо елементи першого стовпця. Спрощено визначник матриці 4х4 можна подати через суму чотирьох детермінантів третього порядку у вигляді
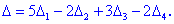
Далі переходимо до відшукання визначників за правилом трикутників
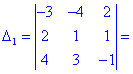
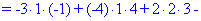
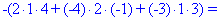
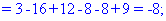
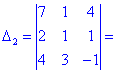
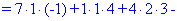
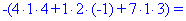
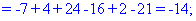
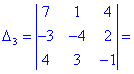
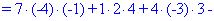
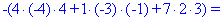
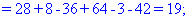
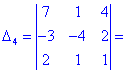
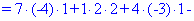
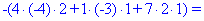
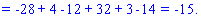
Обчислення не надто складні, головне не напутати зі знаками та при виборі трикутників. Знайдені величини підставляємо в головний визначник матриці та підсумовуємо
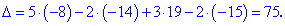
Результат перевіряємо матричним калькулятором YukhymCALC . Правильність розрахунків підтверджується наступним малюнком

Метод зведення визначника до трикутного вигляду
Даний метод дозволяє ряд визначників обчислити в досить швидкий спосіб. Суть його полягає у зведенні визначника до трикутного вигляду, при цьому слід враховувати всі множники на які збільшуємо чи зменшуємо рядки та врахуванні при кінцевих розрахунках. З даного визначення Ви нічого для себе не зрозумієте, тому краще все показати на конкретних прикладах.
Приклад 3. Знайти визначник матриці зведенням до трикутного вигляду
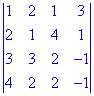
Розв'язання. Спочатку здійснюємо математичні маніпуляції, щоб отримати всі нульові елементи окрім першого в першому стовпці. Для цього від другого рядка віднімаємо перший, помножений на два. В результаті отримаємо
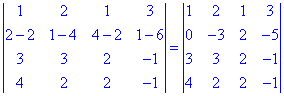
Далі є два варіанти: від третього рядка відняти перший помножений на три, або від третього відняти суму перших двох рядків. Останній варіант дозволить отримати зразу два нулі в рядку, його і вибираємо
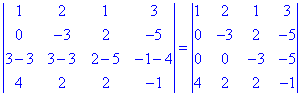
Дальше доцільніше від четвертого відняти подвоєний другий рядок. В результаті елементарних перетворень визначник набуде вигляду
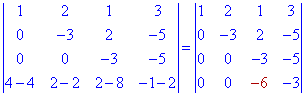
Залишилося перетворити в нуль один елемент в третьому стовпці. Для цього від четвертого рядка віднімаємо подвоєний третій в попередньо записаному визначнику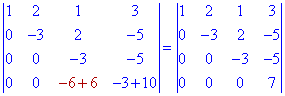
Визначник трикутної матриці рівний добутку діагональних елементів.
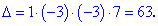
За бажанням можна первірити результат матричним калькулятором. В цьому прикладі ніяких домножень рядків, в яких занулювали елементи ми не виконували, то ж повністю розкрити метод на цьому прикладі не получилося. Розглянемо складніший.
В цьому прикладі ніяких домножень рядків, в яких занулювали елементи ми не виконували, то ж повністю розкрити метод на цьому прикладі не получилося. Розглянемо складніший.
Приклад 4. Знайти визначник матриці 4-го порядку
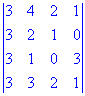 Розв'язання. Елементарними перетвореннями зводимо визначник до трикутного вигляду. Для цього від кожного рядка віднімаємо перший. В результаті перетворень отримаємо наступний детермінант
Розв'язання. Елементарними перетвореннями зводимо визначник до трикутного вигляду. Для цього від кожного рядка віднімаємо перший. В результаті перетворень отримаємо наступний детермінант
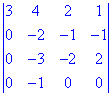
Для зручності обчислень, міняємо третій рядок з другим місцями.

За властивістю визначників, будь-яка заміна рядків місцями веде до зміни знаку визначника. Враховуємо це у деякому множнику k=-1.
Від третього рядка віднімаємо другий, помножений на мінус три. Після спрощень отримаємо

Перетворюємо в нуль останній елемент в другому стовпці, для цього віднімаємо другий рядок помножений на 2. Результат буде наступним

Від подвоєного четвертого рядка віднімаємо третій. За властивістю, домноження рядка на сталу а веде до зміни визначника в а раз. Дану зміну фіксуємо в множнику k=-1*2=-2.

Остаточне значення визначника буде рівне добутку діагональних елементів поділених (або нормованих) на множник k, який відповідає за зміну детермінанта при елементарних перетвореннях. Виконуємо обчислення
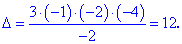
Перевірка матричним калькулятором підтверджує правильність здійснених обчислень. Метод розкладу визначника за елементами рядків чи стовпців доцільно застосоввати при знаходженні детермінантів матриць 4х4 та більих розмірів. Метод зведення до трикутного вигляду ефективний, якщо елементарні перетворення легко прослідкувати і не призводять до великих добутків. В інших випадках потрібно користуватися комбінацією цих методів, останнім утворювати якомога більше нульових елементів, а методом розкладу за рядками чи стовпцями зменшувати кількість виконаних операцій. Це дозволить без проблем обчислювати визначники третього, четвертого і навіть п'ятого порядку.
Метод розкладу визначника за елементами рядків чи стовпців доцільно застосоввати при знаходженні детермінантів матриць 4х4 та більих розмірів. Метод зведення до трикутного вигляду ефективний, якщо елементарні перетворення легко прослідкувати і не призводять до великих добутків. В інших випадках потрібно користуватися комбінацією цих методів, останнім утворювати якомога більше нульових елементів, а методом розкладу за рядками чи стовпцями зменшувати кількість виконаних операцій. Це дозволить без проблем обчислювати визначники третього, четвертого і навіть п'ятого порядку.
Вас може зацікавити:
]]>