Текстові задачі на складання рівнянь взяті із збірника "Тестові завдання для вступників. Математика" ( стор. 84) виданого у 2001 році Волинським державним університетом імені Лесі Українки.
Наведені задачі відповідають рівню підвищеної складності і навчать Вас будувати рівняння та знаходити невідомі величини. Крім того Ви ознайомитеся з простими і ефективними методиками розв'язку рівнянь та системи рівнянь. Відповіді для школярів 9, 10 класів завдання можливо і важкі, а всім хто готується до олімпіади чи вступу стануть хорошим репетитором та помічником.
Приклад1. Порівнюючи два бруски, що мають форму прямокутного паралелепіпеда, з'ясували, що довжина, ширина і висота другого бруска відповідно на 2 см більші, ніж першого, а об'єм та повна поверхня другого бруска відповідно на 138 см3 і 120 см2 більші ніж першого. Яка повна поверхня другого бруска (у см2 )?
Розв'язання:
Задане завдання з попереднім мають однаковий алгоритм обчислень. При однакових позначеннях сторін запишемо рівняння, які слід розв'язати
(a+2)*(b+2)*(c+2)=a*b*c+138;
2*(a+2)(b+2)+ 2*(b+2)*(c+2)+2*(a+2)*(c+2)=S+120.
Потрібно знайти S. Після розкриття дужок та спрощень отримаємо
S+4*(a+b+c)+8=138;
8*(a+b+c)+12=120.
Виразимо з другого рівняння потрібні доданки та підставимо у перше
4*(a+b+c)=120/2-12/2=60-6=54;
S=138-8-54=76 (сантиметрів квадратних).
Відповідь: S=76.
Приклад 2. Шукане трицифрове число починається з цифри 1. Якщо її витерти і потім дописати замість останньої цифри числа, то утворене нове трицифрове число буде більше за шукане на  . Знайте шукане число.
. Знайте шукане число.
Розв'язання:
За властивостями логарифма спростимо число 
Рівняння до задачі матиме вигляд
ab1-1ab=90.
Почнемо розв'язувати його з одиниць
1-b=0; b=1.
Записана умова спроститься до вигляду
a11-1a1=90.
Без обчислень можна здогадатися, що друга цифра рівна a=2.
Отже загадане число рівне 121.
Відповідь: 121.
Приклад 3. По двох сторонах прямого кута в напрямку до його вершини рухаються два тіла. В початковий момент тіло А знаходиться від вершини прямого кута на відстані 60м, а тіло В - на відстані 80м. Через 3с відстань між А і В стала рівною 70м, а ще через 2с – 50м. Знайти швидкість тіла А (в м/с).
Розв'язання:
Рівняння руху тіл можна записати формулою
60-V[a]*t;
80-V[b]*t.
Оскільки вони рухаються по сторонах прямого кута то відстань між ними знаходимо за теоремою Піфагора. В результаті отримаємо два рівняння для знаходження невідомих швидкостей 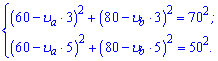
Потрібно виразити з довільного із рівнянь швидкість тіла В і підставити в інше. В результаті отримаємо ірраціональне рівняння відносно V[a]. Ми окрім складання рівнянь маємо на меті навчити Вас використовувати математичні пакети. В Мейплі розв'язок системи рівнянь можна знайти одним рядком коду, а за розв'язування рівнянь відповідає команда solve.
> restart;
> solve({(60-V[a]*3)^2+(80-V[b]*3)^2=70^2,(60-V[a]*5)^2+(80-V[b]*5)^2=50^2},{V[a],V[b]})
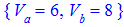
З відповіді бачимо, що шукана швидкість рівна 6 метрів за секунду.
Відповідь: 6 м/с.
Приклад 4. Свіжі огірки, які містять 98% води, важили 100 кг. Коли огірки підсохли, то води в них стало 96%. Скільки стали важити огірки після підсихання (в кілограмах)?
Розв'язання:
Обчислимо скільки сухої маси в огірках
100*(100-98)/100=2 (кг).
Підсохлі огірки мають 96 % води і (100-96)=4 % води.
Складемо пропорцію
2 – 4 %
X – 100%
З якої знайдемо повну масу підсохлих огірків
X=100*2/4=50 (кг).
Подібним чином шукають відповіді і в задачах про гриби, яблука, груші, сливи і тому подібне, тому запам'ятайте просту схему обчислень.
Відповідь: 50 кг.
Приклад 5. Бджоли, переробляючи квітковий нектар в мед, звільняють його від значної кількості води. Скільки кілограмів нектару доводиться переробляти бджолам для отримання 1 кг меду, коли відомо, що нектар містить 75% води, а отриманий з нього мед -17 % води?
Розв'язання:
Отже відомо, що нектар містить 75 % води, мід – 17%.
Знайдемо кількість 100 % меду
1 – 100%
X – (100-17)%.
X=83/100=0, 83 (кг).
В нектарі це становить (100-75)=25 % маси. Складаємо 2 пропорцію для обчислення маси всього нектару
0,83 – 25%
Y – 100%.
Виконаємо обчислення
Y=0,83*100/25=3,32 (кг).
Отже для отримання 1 кг меду бджоли мають переробити 3, 32 кг нектару.
Як бачите обчислення не складні, головне – зрозуміти принцип запису пропорцій.
Приклад 6. Три тракторні бригади разом зорюють поле за 4 дні. Це ж поле перша і друга бригади разом можуть зорати за 6 днів, а перша і третя разом - за 8 днів. У скільки разів площа, яку зорює за день друга бригада більша від площі, яку зорює за день третя бригада?
Розв'язання:
Задачі на спільну роботу даються багатьом важко, оскільки не всі розуміють, як скласти рівняння? Проте потрібно користуватися загальними формулами: "продуктивність" помножити на "час" = "робота".
Складаємо відповідні рівняння
(a+b+c)*4=A;
(a+b)*6=A;
(a+c)*8=A.
З запису можна здогадатися, що a, b, c –продуктивність 1, 2, 3 бригад; A – умовне позначення поля.
Запишемо отриману систему рівнянь так щоб продуктивність в лівій стороні рівнянь була без часу 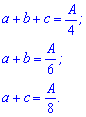
Для відшукання продуктивності бригад, про які запитують від 1 рівняння віднімемо 2 і (1-3). В результаті отримаємо 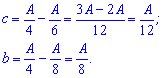
У скільки разів більша площа означає, що потрібно b/c. 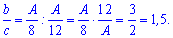
Отже відповідь: у 1,5 рази друга бригада зорює більше поля ніж третя.
Приклад 7. Дві точки, рухаючись по колу в одному напрямку, зустрічаються через кожні 56 хв; рухаючись в протилежних напрямках - через кожні 8 хв. Знайти швидкість першої точки (в м/хв), коли відомо, що за 1 с. перша точка проходить на 1/12 м більше, ніж друга.
Розв'язання:
Спочатку переведемо шлях пройдений за 1 секунду в швидкість – 1/12 м/с.
У потрібній системі одиниць ця швидкість становитиме 1.12*60=5 метрів за хвилину.
Введемо позначення, нехай перша точка рухається зі швидкістю V, тоді швидкість другої – V-5. Таке позначення зручне для обчислень, оскільки при розв'язанні рівнянь зразу знаходимо потрібну швидкість.
Рухаючись по колу швидша з точок проходить повне коло S і частину другого до зустрічі з другою точкою. У рівняннях це матиме запис
V*56=S+(V-5)*56;
V*56-(V-5)*56=S.
Рухаючись в протилежних напрямах вони зустрічаються кожні 8 хвилин. Це означає, що в сумі кожні 8 хвилин вони проходять коло, тобто
V*8+(V-5)*8=S.
Віднімемо від першого рівняння 2, щоб позбутися довжини кола S.
V*(56-8)-(V-5)*(56+8)=0;
V*48-V*64+64*5=0;
16*V=64*5;
V=64/16*5=4*5=20 (м/хв).
Добре розберіть схему розв'язку задачі на рух по колу, багатьом їх важко зрозуміти і вирішити.
Відповідь: 20 м/хв.
Приклад 8. Дві точки, рухаючись по колу в одному напрямку, зустрічаються через кожні 56 хвилин. Знайти довжину кола (в метрах), коли відомо, що за 1 секунду перша точка проходить на 1/12 метра більше, ніж друга.
Розв'язання:
До обчислення рівнянь схема аналізу задачі один в один повторює попередній приклад.
Далі з одного рівняння потрібно виразити швидкість через шлях і підставити у друге рівняння. Оскільки швидкість нам відома, то підставимо її у друге рівняння попереднього прикладу
S=16*V-40=16*20-40=280 (метрів).
Відповідь: довжина кола 280 метрів.
Переглянути схожі матеріали:


