Логарифмічні та показникові рівняння та нерівності починають вивчати в 9-11 класах і продовжують у ВУЗах. Самі по собі схеми розв'язку рівнянь, як і нерівностей, базуються на властивостях показникових функцій та логарифмів. В більшості випадків за допомогою нехитрих схем все зводиться до лінійних та квадратних рівнянь, які до того часу повинні навчитися розв'язувати усі.
РІВНЯННЯ
Приклад 1. Розв'язати рівняння log0,35=log0,3(3-2*x)
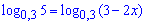
Розв'язання: Виписуємо обмеження на область допустимих значень логарифма (ОДЗ):
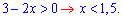
Наступним кроком при рівних основах прирівнюємо вирази під логарифмами
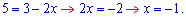
Значення x=-1 задовільняє ОДЗ, отже є розв'язком логарифмічного рівняння.
Приклад 2. Знайти розв'язки показникового рівняння
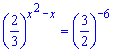Розв'язання: Перетворюємо праву сторону, щоб отримати справа і зліва від знаку рівності однакові основи в степенях
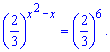
Далі при рівних основах прирівнюємо показники
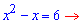
В результаті прийдемо до квадратного рівняння
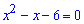
корені якого знаходимо за теоремою Вієта
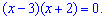
Розв'язками показникового рівняння є значення x=-2; x=-3.
Приклад 3. Знайти корені логарифмічного рівняння
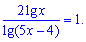Розв'язання: Серед обмежень на ОДЗ слід відзначити наступні: в чисельнику змінна під логарифмом повинна бути більшою нуля, те саме стосується і знаменника. Також знаменник дробу не повинен дорівнювати нулю. Всі ці умови можемо записати системою нерівностей, з яких і визначаємо ОДЗ
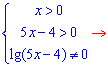
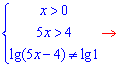
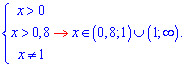
На знайдених інтервалах шукаємо розв'язок рівняння. Перепишемо його у вигляді
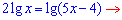
За властивістю логарифма вносимо множник під логарифм
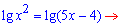
При рівних основах логарифма прирівнюємо функції
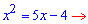
В результаті прийдемо до квадратного рівняння
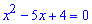
розв'язок якого за теоремою Вієта рівний x=1; x=4.
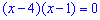
Перший корінь не задовільняє ОДЗ, залишається єдиний розв'язок рівняння x=4.
Приклад 4. Розв'язати рівняння
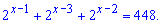Розв'язання: Зліва від знаку рівності маємо кілька доданків, що місять двійку в певному показнику. Є два способи спрощення - або виділити найстарший доданок або наймолодший та згрупувати доданки, що залишаться. В результаті перетворимо показникові рівняння до простого вигляду
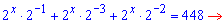
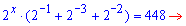
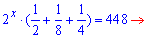
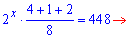
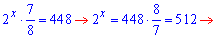
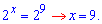
Значення x=9 є розв'язком показникового рівняння.
НЕРІВНОСТІ
Приклад 5. Розв'язати нерівність
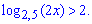
Розв'язання: Логарифмічну нерівність записуємо у вигляді системи двох нерівностей. Перша нерівність це умова на область допустимих значень, друга – рівняння перетворене з логарифмічного (за властивістю логарифма)
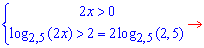
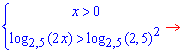
Основа логарифма більша одиниці, тому розкриваємо нерівність без зміни знаку нерівності
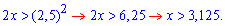
Знайдене значення не суперечить ОДЗ, таким чином розв'язком логарифмічного рівняння є інтервал
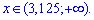
Приклад 6. Знайти розв'язок нерівності
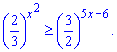
Розв'язання: Зведемо праву сторону нерівності до тієї ж основи, що і зліва
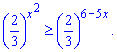
Для цього показник помножили на мінус одиницю та обернули основу. Далі, оскільки основа показника менша одиниці то при розкритті нерівності знак змінюємо на протилежний. Прийдемо до квадратичної нерівності
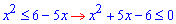
корені якої, використовуючи теорему Вієта, розписуємо через прості множники
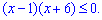
Підставивши значення із середини проміжку x=0 переконуємося, що нерівність виконується між коренями. Розв'язком нестрогої нерівності є проміжок [-6; 1].
Приклад 7. Розв'язати нерівність
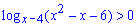Обчислення: Задано логарифмічну нерівність, навіть можна сказати, що дві в одній. Оскільки в основі маємо функцію то в залежності чи вона приймає значення більше одиниці чи менше нерівність трансформується на дві. Спершу розглянемо випадок коли основа більша одиниці. Записуємо обмеження на ОДЗ та розкриваємо нерівність
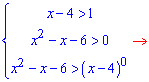
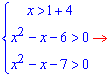
Не вдаючись в деталі розписуємо останню нерівність за Теоремою Вієта
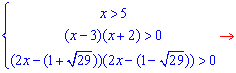
Звідси розв'язком є інтервал
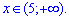
Тепер розглянемо ІІ випадок, коли основа є в межах від нуля до одиниці. При розкритті логарифма знак змінюємо на протилежний
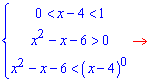
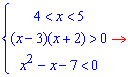
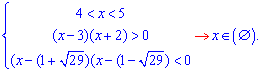
На цьому інтервалі нерівність немає розв'язків. Правильна відповідь до завдання – інтервал від 5 до плюс безмежності
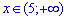
Приклад 8. Розв'язати нерівність
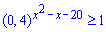Обчислення: За властивістю показників перетворимо праву сторону нерівності
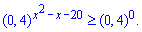
Далі, оскільки основа 0,4<1 менша одиниці - змінюємо знак на протилежний при розкритті нерівності
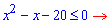
Квадратичну нерівність за теоремою Вієта спрощуємо до вигляду
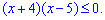
Підстановкою нуля перевіряємо, що нерівність виконується між коренями. Звідси відповіддю є проміжок [-4; 5].
Приклад 9. Розв'язати нерівність
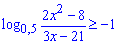Розв'язання: ОДЗ логарифма знаходимо з умови, що дробова функція додатно визначена
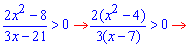
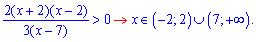
ОДЗ складається з двох інтервалів. Далі розписуємо праву сторону логарифмічної нерівності
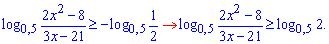
Оскільки основа логарифма менша одиниці то змінюємо знак при розкритті нерівності
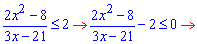
Далі все як із нерівностями зі шкільного курсу математики – переносимо доданки по один бік нерівності, зводимо до спільного знаменника, обчислюємо
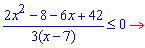
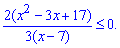
Чисельник нерівності завжди більший нуля. Це слідує з того, що дискримінант квадратного рівняння менший нуля, а вільний член додатний. Отже нерівність має місце коли знаменник від'ємний, а це дає умову x<7. Враховуючи ОДЗ, розв'язком нерівності буде інтервал (-2; 2).
Логарифмічні та показникові рівняння та нерівності в Maple
Даний матеріал в першу чергу стосується студентів і мета не тільки навчити Вас математичного пакету Maple для обчислення рівнянь, а перш за все для перевірки результатів обчислень. Перша команда restart занулює всі змінні. Для обчислення рівнянь всіх типів (логарифмічні, показникові, дробові, квадратні, тригонометричні) використовуємо команду solve. Записуємо рівняння і яку змінну слід обчислити
>restart;
> solve(log[0.3](5)=log[0.3](3-2*x),x);
В результаті отримаємо
-1.000
Для обчислення показникового рівняння з 4 прикладу достатньо ввести наступний рядок коду та натиснути "Enter".
> solve(2^(x-1)+2^(x-3)+2^(x-2)=448,x);
У відповіді отримаємо 9.
З таким самим успіхом можемо розв'язувати у Мaple логарифмічні та показникові нерівності.
Для розв'язування прикладу 6 слід ввести запис
> solve((2/3)^(x^2)>=(2/3)^(-5*x+6),x);
Результатом обчислень буде проміжок
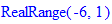Приклад 8 можемо обчислити, ввівши код
> solve(0.4^(x^2-x-20)>=1,x);
У відповідь отримаємо проміжок
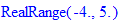Але і "мейплу" не завжди слід довіряти, тому що бувають випадки коли отримуємо зайві корені або недостачу потрібних. Тому спершу розв'язуємо на листку, а лише тоді перевіряємо. Також уважно слідкуйте за кількістю відкритих і закритих дужок в Мейплі - це є найтиповіша помилка при наборі формул.
Більше прикладів на логарифмічні та показникові рівняння шукайте на сторінках сайту. Якщо зустрінете завдання з яким важко впоратися самотушки, то надсилайте такі завдання нам. Ми їх систематизуємо і зробимо цікаву та корисну для школярів та студентів статтю.
