Розберемо відповіді до тестових прикладів на властивості трапеції. Тут маємо рівнобічну, прямокутну, загальної форми трапеції.
В завданнях потрібно знайти сторони, основи, середню лінію, площу та периметр.
На простих прикладах Ви зможете пригадати шкільну програму з геометрії за 9,10 класи.
Пояснення до задач допоможуть Вам підготуватися до ЗНО тестів з математики.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Зміст: В книзі наведені рекомендації щодо проходження ЗНО з математики та зразки тестових завдань.
Завдання кожної з тем розміщені в порядку зростання складності.
Рекомендуємо всім переглянуи готові відповіді до посібника, що розміщені на сайті, а також самостійно пройти теми, з якими маєте труднощі на практичних.
Тема 32. Чотирикутники
Задачі на властивості трапеції
Приклад 32.11 Висота рівнобічної трапеції, яка проведена з вершини тупого кута, поділяє основу на відрізки завдовжки 5 см і 11 см.
Знайти периметр трапеції, якщо її висота дорівнює 12 см.
Обчислення: Далі дамо прості рекомендації як обчислювати задачі та як їх оформляти.
Всюди де це потрібно виконуйте побудову рисунків, в зошитахв клітинку чи на А4 форматі немає значення.
На малюнках позначайте сторни, кути, висоти, діагоналі - все що є задано та дає хоч якусь підказку до правильного ходу обчислень.
Після цього, як маємо рисунок перед очима можемо переходити до пояснень.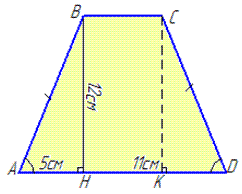
Нехай задано рівнобічну трапецію ABCD, основи паралельні AD||BC, сторони AB=CD рівні між собою, BH⊥AD, де BH=12 см – висота трапеції, опущена на сторону AD,
AH=5 см, HD=11 см, звідси AD=AH+HD=5+11=16 см.
Розглянемо прямокутний трикутник ABH (∠AHB=90) та знайдемо за формулою Піфагора гіпотенузу AB:
AB^2=AH^2+BH^2, звідси
Оскільки трапеція ABCD – рівнобічна, то відповіні сторони рівні CD=AB=13 см.
Опустимо ще одну висоту CK на сторону AD, тоді кут прямий CK⊥AD (∠CKD=90).
Розглянемо прямокутні трикутники ABH і KCD.
У них ∠BAH=∠CKD – як кути при основі AD у рівнобічній трапеції ABCD (за властивістю), і CD=AB=13 см.
Тому, за ознакою рівності прямокутних трикутників, трикутники ABH і KCD рівні (за гіпотенузою і гострим кутом), звідси слідує AH=KD=5 см.
Тоді у рівнобічній трапеції:
HK=HD-KD=11-5=6 см, тому BC=HK=6 см.
Знайдемо периметр рівнобічної трапеції ABCD:
P=AB+BC+CD+AD=13+6+13+6=48 см.
Відповідь: 48 см – В.
Приклад 32.12 Дві менші сторони прямокутної трапеції дорівнюють a, а один з її кутів – 450.
Визначити площу трапеції.
Обчислення: Наведемо рисунок прямокутної трапеції
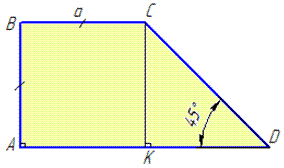У трапецію ABCD відомо: AD||BC, AB⊥AD, AB=BC=a – менші сторони трапеції, ∠ADC=45 (як єдиний гострий кут прямокутної трапеції).
Оскільки бічна сторона перпендикулярна до основи AB⊥AD, то AB=a – висота прямокутної трапеції.
Опустимо ще одну висоту CK на сторону AD, тобто CK⊥AD (∠CKD=90).
Очевидно, що вона також рівна заданій стороні CK=AB=a.
У прямокутному трикутнику KCD (∠CKD=90, ∠CDK=45), тому ∠DCK=45 (за сумою кутів трикутника), і робимо висновок,що трикутник ΔKCD – рівнобедрений.
Тобто, CK=DK=a (тут AK=BC=a як протилежні сторони квадрата ABCK).
Звідси AD=AK+KD=a+a=2a.
Знайдемо площу прямокутної трапеції:
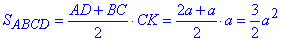
Цю площу можна було знайти в легший спосіб, розписавши як суму площ квадрата S[ABCK]=a^2 і прямокутного трикутника S[kcd]=a^2/2
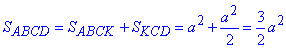
Відповідь: 3/2•a^2 – Д.
Приклад 32.15 Точка O, яка є перетином діагоналей трапеції ABCD (AD||BC), ділить діагональ AC на відрізки AO=8 см і AC=4 см.
Знайти основу BC, якщо AD=14 см.
Обчислення: Нехай маємо трапецію ABCD, AD||BC, AD=14 см, AC=4 см, AO=8 см, де AC і BD – діагоналі трапеції ABCD, які перетинаються в точці O.
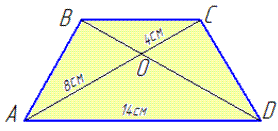
Розглянемо трикутники AOD і COB.
В них ∠AOD=∠COB як вертикальні.
∠OAD=∠OCB і ∠ADO=∠CBO як внутрішні різносторонні кути при перетині січною AC паралельних прямих AD і BC.
Звідси слідує, що ΔAOD~ΔCOB (тобто трикутники подібні за трьома кутами).
З цього слідує, що їх відповідні сторони пропорційні, тобто
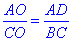
звідси
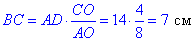
Отже, BC=7 см – основа трапеції.
Відповідь: 7 см – В.
Приклад 32.16 Менша основа трапеції дорівнює 20 см. Точка перетину діагоналей віддалена від основ на 5 і 6 см.
Знайдіть площу трапеції.
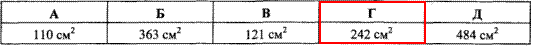
Обчислення: До умови задано рисунок, який має вигляд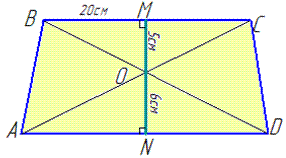 
Для трапеції записуємо все що на момент прочитання умови відомо:
AD||BC, BC=20 см, MO=5 см, ON=8 см, де AC і BD – діагоналі трапеції ABCD, які перетинаються в точці O, MO та ON – відстані від точки O до основ трапеції BC і AD, відповідно (тобто MO⊥BC, ON⊥AD).
Розглянемо трикутники AOD і COB. В них ∠AOD=∠COB як вертикальні.
∠OAD=∠OCB і ∠ADO=∠ CBO як внутрішні різносторонні кути при перетині січною AC паралельних прямих AD і BC.
Звідси робимо висновок, що ΔAOD~ΔCOB (тобто трикутники подібні за трьома кутами).
З цього слідує, що їх відповідні сторони (а значить і висоти MO та ON цих трикутників) пропорційні, тобто
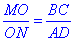
звідси
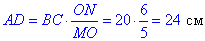
Оскільки MO⊥BC, ON⊥AD, то MN⊥AD (або MN⊥BC), звідси слідує, що MN – висота трапеції (тобто точки M, O і N лежать на одній прямій).
Отже, MN=MO+ON=5+6=11 см.
Знайдемо площу трапеції:
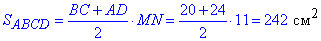
Відповідь: 242 см2 – Г.
Приклад 32.17 Відстань між серединами діагоналей трапеції дорівнює 7 см, а менша її основа – 6 см. Знайти середню лінію трапеції.
Обчислення: Наведемо позначення основ та сторін в трапеції AD||BC, BC=6 см, KL=7 см, де AC і BD – діагоналі трапеції, які перетинаються в точці O, KL – відстань між серединами діагоналей.
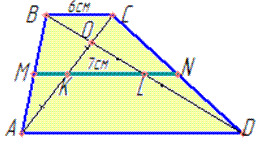
Оскільки KL сполучає середини діагоналей трапеції, то KL є частиною відрізка MN, що з'єднує середини бічних сторін трапеції, тому MN– середня лінія трапеції (це твердження доводиться на основі подібності трикутників:
ΔABC~ΔAMK і ΔDBC~ΔDLN за трьома кутами).
Розглянемо трикутник ABC.
Відрізок MK з'єднує середини сторін AB і AC.
Тому MK – середня лінія трикутника і за властивістю:
MK||BC, а також MK=BC/2=6/2=3 см.
Розглянемо трикутник DBC.
Відрізок LN з'єднує середини сторін BD і CD.
Тому LN – середня лінія трикутника і за властивістю:
LN||BC, а також LN=BC/2=3 см.
Отож, обчислимо середню лінію MN трапеції ABCD
MN=MK+KL+LN=3+7+3=13 см.
Відповідь: 13 см – Д.
Приклад 32.19 Діагоналі рівнобічної трапеції перпендикулярні. Знайти площу трапеції, якщо її основи дорівнюють 8 см і 20 см.
Обчислення: Введемо наступні позначення в рівнобічній трапеції ABCD, AD||BC, BC=8 см, AD=20 см, AB=CD, AC⊥BD, де AC, BD – діагоналі рівнобічної трапеції.
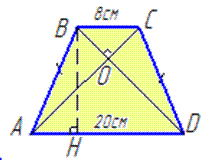
Оскільки у рівнобічній трапеції діагоналі перетинаються під прямим кутом AC⊥BD, то висота BH трапеції (BH⊥AD) дорівнює середній лінії трапеції, тобто півсумі її основ:
BH=(BC+AD)/2 (це твердження потребує доведення!!!).
Знаходимо висоту трапеції BH=(8+20)/2=14 см.
За висотою обчислюємо площу трапеції:
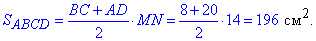
Відповідь: 196 см2 – А.
Приклад 32.22 Діагональ трапеції поділяє її на два подібні трикутники. Знайти цю діагональ, якщо основи трапеції дорівнюють 50 см і 72 см.
Обчислення: Нехай маємо трапецію ABCD, AD||BC, BC=50 см, AD=72 см, AC – діагональ трапеції, яка розбиває її на подібні трикутники ABC і CDA (за умовою).
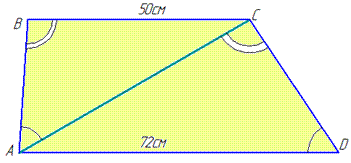
За ознакою подібності у трикутників ABC і CDA відповідні кути рівні:
∠ACB=∠CAD (як внутрішні різносторонні кути при перетині січною AC паралельних прямих AD і BC);
∠BAC=∠ADC, ∠ABC=∠ACD.
На основі теореми синусів запишемо рівність для визначення діагоналі AC:
Для трикутника ΔABC складаємо пропорцію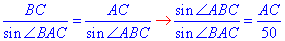 
(*).
У трикутнику ΔABC маємо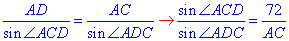 
Однак маємо два рівні кути ∠BAC=∠ADC і ∠ABC=∠ACD, тому формули вище перепишемо до вигляду
(**).
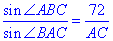Прирівняємо вирази (*) і (**) і знайдемо діагональ AC:
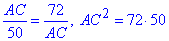
звідси AC^2=3600, AC=60 см.
Відповідь: 60 см – Д.
Приклад 32.28 У рівнобічних трапеціях діагональ є бісектрисою гострого кута й утворює з більшою основою кут 30.
Установити відповідність між довжинами більших основ (1–4) та периметрами трапецій (А–Д).
1. 4 см
2. 8 см
3. 24 см
4. 12 см
А. 20 см
Б. 60 см
В. 10 см
Г. 30 см
Д. 50 см.
Обчислення: Умова задачі збігається з умовою задачі 32.23 (дивись її розв'язок).
Знайдемо периметри трапецій в залежності від значень більшої основи AD:
1) 
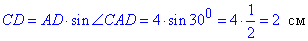
звідси AB=BC=CD=2 см і AD=4 см.
P=AB++BC+CD+AD=3·2+4=10 см. – В
2) 
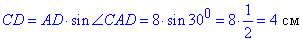
звідси AB=BC=CD=4 см і AD=8 см.
P= 3·4+8=20 см. – А.
3) 
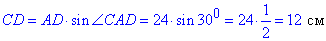
звідси AB=BC=CD=12 см і AD=24 см.
P= 3·12+24=60 см. 3 – Б.
4) 
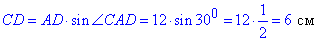
звідси AB=BC=CD=6 см і AD=12 см.
P= 3·6+12=30 см. 4 – Г.
Приклад 32.23 У рівнобічній трапеції діагональ є бісектрисою гострого кута й утворює з більшою основою кут 300. Знайти периметр трапеції, якщо більша основа дорівнює 8 см.
Обчислення: Нехай маємо рівнобічну трапецію ABCD, AD||BC, AD=8 см, AB=CD, ∠CAD=30, де AC – діагональ (і бісектриса ∠A) рівнобічної трапеції, тому ∠BAC=∠CAD=30.
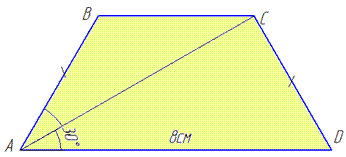
Зразу можемо знайти повні кути при основі ∠A=∠D=∠BAC+∠CAD=30+30=60 оскільки у рівнобічної трапеції кути при основі рівні.
∠BCA=∠CAD=30 (як внутрішні різносторонні кути при перетині січною AC паралельних прямих AD, BC).
Звідси ∠BCA=∠BAC=30, тому трикутник ABC – рівнобедрений з основою AC і AB=BC – бічні сторони ΔABC.
Отже, можемо записати рівність трьох сторін AB=BC=CD, оскільки трапеція рівнобедрена (за умовою).
Розглянемо трикутник ACD, у якого AD=8 см, ∠CAD=30 і ∠D=60.
За теоремою про суму кутів трикутника знайдемо ∠CAD:
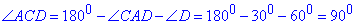
Отже, трикутник ACD – прямокутний з катетами AC і CD.
За означенням синуса гострого ∠CAD знайдемо катет CD:
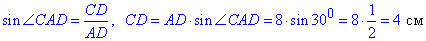
Отже, маємо AB=BC=CD=4 см і AD=8 cм
Знайдемо периметр трапеції:
P=3•4+8=20 см.
Відповідь: 20 см – Г.
На цьому завдання на чотирикутники розв'язані, умови не можна віднести до простих, але саме на таких задачах Ви найшвидше вчитеся.
Гарних Вам результатів на іспитах та при вступі у ВУЗи!
