Приклади на визначення кутів у колі чи крузі надзвичайно багато. В школі в молодших класах простіші, далі такі як тут приведені.
Завдання підібрано із курсу підготовки до ЗНО з математики, тому можете зразу перевірити свої сили та побачити, що Вас чекатиме у ВУЗах на спеціальностях з математичним нахилом.
Задача 34.5 Яка кутова величина дуги завдовжки π /2 см у колі радіуса 3 см?
А | Б | В | Г | Д |
150 | 300 | 450 | 600 | 750 |
Розв'язання: Кут будемо виводити з формули для обчислення довжини дуги кола:
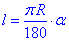 , де
, де 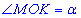 - відповідний центральний кут;
- відповідний центральний кут;
l=π/2 см - довжина дуги кола.
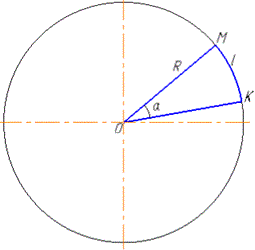
OM=OK=R=3 см - радіус кола.
Виводимо формулу кута через довжину дуги та радіус та обчислюємо
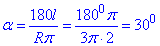
Відповідь: 300 – Б.
Задача 34.9 На рисунку зображено коло з центром у точці O і рівносторонній трикутник AOB, що перетинає коло в точках M і N.
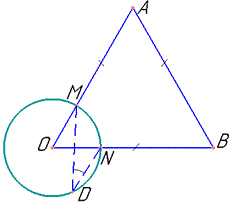
Точка D належить колу. Знайти градусну міру кута MDN.
А | Б | В | Г | Д |
2π см2 | 3π см2 | 4π см2 | 5π см2 | 6π см2 |
Розв'язання: Маємо рівносторонній трикутник AOB з внутрішнім кутом 600, тобто ∠AOB=60.
Маємо коло з центром у точці O, яке перетинає трикутник в точках M і N, звідси ∠MON=∠AOB=60 (∠MON - центральний кут, який спирається на дугу MN).
Точка D належить колу, тому ∠MDN - вписаний кут, який також спирається на дугу MN, тому за властивістю (вписаний кут дорівнює половині центрального кута, які спираються на одну й ту ж саму дугу) маємо:
∠MDN=∠MON/2=60/2=30.
Властивості вписаного кута, яка тут допомогла вирішити задачу Вт мабуть не знаєте, тож ще раз перечитайте та запам'ятайте.
Відповідь: 300 – Б.
Задача 34.9a Площа кругового сектора радіуса 6 см дорівнює 5π см2. Знайти кутову величину дуги.
А | Б | В | Г | Д |
150 | 300 | 450 | 600 | 750 |
Розв'язання: Виведемо кут через формулу для обчислення площі кругового сектора:
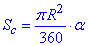 , де
, де 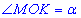 - кутова величина дуги;
- кутова величина дуги;
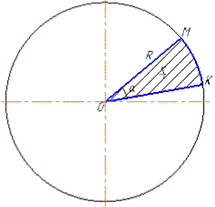
OM=OK=R=6 см - радіус круга;
SC=5π см2 - площа кругового сектора, звідси
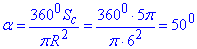
Відповідь: 500 – Б.
Задача 34.12 До кола проведено дотичну AB (B - точка дотику) та січну AC, що проходить через центр O кола.
Знайти градусну міру кута COB, якщо ∠OAB=35.
А | Б | В | Г | Д |
1050 | 1150 | 1200 | 1250 | 1450 |
Розв'язання: За властивістю кола: дотична до кола в точці дотику перпендикулярна до радіуса цього кола, тому OB - радіус кола і ∠ABO=90.
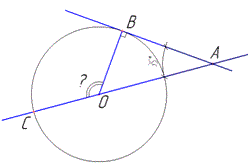
У ΔAOB маємо ∠OAB=35 і ∠ABO=90 - внутрішні кути, а ∠COB - зовнішній кут, який не суміжний з двома внутрішніми, тому за властивістю кутів трикутника, отримуємо
∠COB=∠OAB+∠ABO=35+90=125.
Відповідь: 1250 – Г.
Задача 34.12a Площа кругового сектора становить 15% площі круга.
Яка величина центрального кута сектора?
А | Б | В | Г | Д |
300 | 450 | 540 | 150 | 200 |
Розв'язання: Частина круга (сектор), яку обмежує дуга з центральним кутом alpha обчислюємо за формулою:
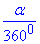 (дивись рис. 34.8-9а). За умовою, площа сектора 15%, тобто 0,15, отже
(дивись рис. 34.8-9а). За умовою, площа сектора 15%, тобто 0,15, отже
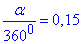 , звідси
, звідси 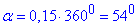
Відповідь: 540 – В.
Задача 34.13 Коло, радіус якого дорівнює 9, розігнуто в дугу, радіус кола якої дорівнює 24.
Знайти центральний кут, який стягує утворену дугу.
А | Б | В | Г | Д |
1000 | 1200 | 1350 | 1500 | 1800 |
Розв'язання: Маємо коло з радіусом R1=9, яке потім розігнули у дугу, радіус кола якої R2=24 і центральним кутом alpha.
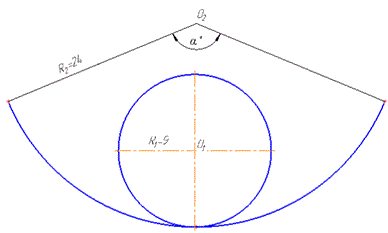
Очевидно, що довжина утвореної дуги l дорівнює довжині заданого кола.
Знайдемо довжину заданого кола:
l=2πR1=2π•9=18π.
Довжину дуги l з центральним кутом alpha і радіусом кола R2 можна обчислити за формулою:
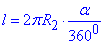
звідси виводимо формулу кута
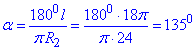
Відповідь: 1350 – В.
Задача 34.14 Точки A, B і C ділять коло на дуги у відношенні 2:3:4.
Знайти найбільший кут трикутника ABC.
А | Б | В | Г | Д |
1600 | 800 | 1200 | 1000 | 700 |
Розв'язання: Градусна міра всього кола дорівнює 3600.
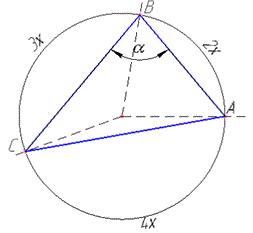
Нехай градусні міри дуг дорівнюють 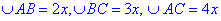 , де x - коефіцієнт пропорційності, тоді
, де x - коефіцієнт пропорційності, тоді
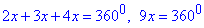 , звідси знаходимо коефіцієнт x=40.
, звідси знаходимо коефіцієнт x=40.
Далі перераховуємо кути дуг
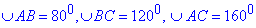
Внутрішні кути ΔABC є вписаними кутами у коло і дорівнюють половині дуги, на яку вони спираються.
Найбільшим кутом ΔABC є кут B, оскільки він спирається на найбільшу дугу AC, тому
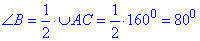
Відповідь: 800 – Б.
Сподіваюсь, пояснення до розв'язків задач на кути в колі для Вас цілком зрозумілі. Формул та властивостей кутів у колі не так багато, але на їх основі можна привести ще безліч задач, які не ввійшли сюди з об'єктивних причин. Далі розглянемо приклади на знаходження площі круга, сегмента, сектора.


