Рядом Тейлора для функции f(x) при условии, что она определена в окрестности точки a, а также ее конечные производные любого порядка называется ряд вида
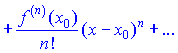
Пусть сумма ряда задана формулой
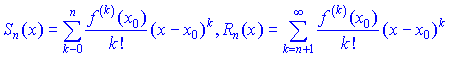
тогда формула Тейлора имеет вид
Бесконечно дифференцируема функция f(x) на интервале
При нулевом значении
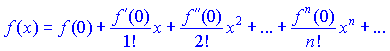
РАСПИСАНИЕ В РЯД МАКЛОРЕНА ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
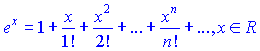
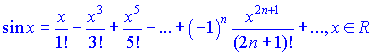
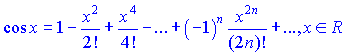
![]()
![]()
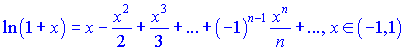
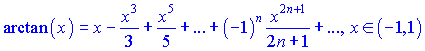
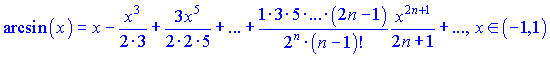
--------------------------------------------
Пример 1. Развить в ряд Тейлора функцию (9.293)
![]() по степеням
по степеням ![]()
Решение. Разложение по степенях множителя ![]() следует понимать, как расписание в точке
следует понимать, как расписание в точке ![]() Вычислим значения функции и ее производных в этой точке
Вычислим значения функции и ее производных в этой точке
![]()
![]()
![]()
![]()
![]()
Подставляем полученные значения в ряд Тейлора
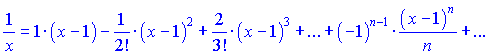
Упрощенно ряд можно записать в виде суммы
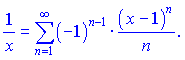
Исследуем сходимость полученного ряда по признаку Деламбера
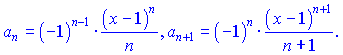
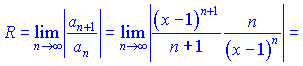
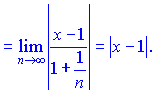
Из условия![]() находим область сходимости
находим область сходимости
![]()
Исследуем границы интервала. При значении ![]() ряд
ряд
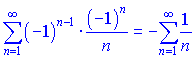
превращается в гармоничный со знаком минус. Этот ряд расходится. При ![]() получим знакопочережний ряд вида
получим знакопочережний ряд вида
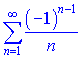
который убывает.
Таким образом, областью сходимости ряда является ![]() . Исследуя остаточный член ряда
. Исследуя остаточный член ряда
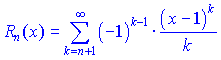
формулы Тейлора для данной функции, убеждаемся, что в заданном интервале ряд совпадает и остаточный член ряда существенного вклада при больших ![]() не вносит.
не вносит.
--------------------------------------------
Пример 2. Развить в ряд Маклорена функцию (9.305)
![]()
Решение. Воспользовавшись первой из формул расписания элементарных функций, получим
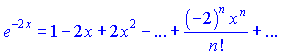
Умножая на ![]() , получим расписание заданной функции в виде такого ряда
, получим расписание заданной функции в виде такого ряда
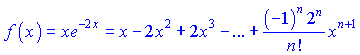
или в упрощенной форме
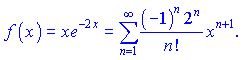
По признаку Деламбера найдем область сходимости ряда
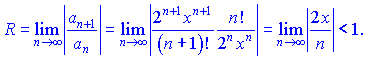
То есть, радиусом сходимости будет интервал ![]() .
.
На этом знакомство с темой подходит к концу. Больше материалов Вы найдете в категории "Ряды".
Рассмотрим примеры применений рядов Тейлора к приближенным вычислениям.
--------------------------------------------
Пример 1. Вычислить с точностью до 0,0001
1) ![]()
2) (9.331) ![]()
3) (9.333) ![]()
4) (9.333) 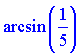
Решение. 1) Запишем заданную функцию в удобном виде
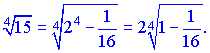
Воспользуемся формулой разложения в ряд Тейлора
![]()
и выпишем несколько членов ряда при степенях аргумента
![]()
В результате получим значение
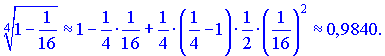
Согласно записанной выше формуле, умножаем полученное число на 2
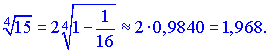
2) ![]()
Воспользуемся разложением синус функции в окрестности нуля
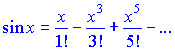
Заданное выражение перепишем в следующей форме
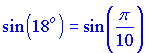
и подставим в формулу
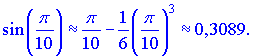
Взяв только два члена ряда получаем достаточно хорошую сходимость. И такая сходимость бывает не всегда. Чем дальше отдаляемся от точки в которой развит ряд, тем больше членов разложения нужно брать для точности результата.
3) ![]()
Выпишем разложение логарифма около единицы
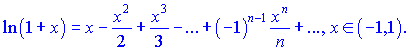
В данном случае подставим ![]() и просуммируем несколько членов ряда
и просуммируем несколько членов ряда
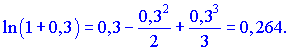
Точный результат равный
![]()
Для обеспечения сходимости с точностью 0,0001 нужно брать больше членов ряда
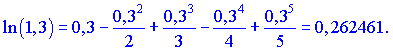
Получили хорошую сходимость, но пришлось брать пять членов разложения в ряд. Это связано с тем что точка в которой искали приближенное значение находится далеко от точки разложения ряда.
4) 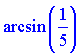
Пусть имеем разложение арксинуса возле нуля
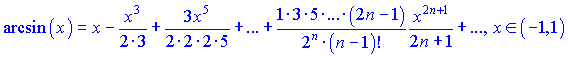
Точное значение будет следующим
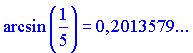
Взяв два члена ряда
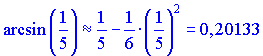
получим хорошую сходимость.
По аналогии с прведенными примерами поступаем и для ряда других функций.
Пример 1.4 Вычислить сумму рядов:
а)
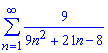
Вычисления: Поскольку граница общего члена ряда при номере следующему до бесконечности равна 0
то данный ряд сходится. Вычислим сумму ряда. Для этого преобразуем общий член, разложив его на простейшие дроби I и II типа. Методика разложения на простые дроби здесь приводиться не будет (хорошо расписана при интегрировании дробей), а лишь запишем конечный вид разложения
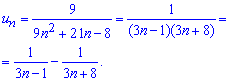
В соответствии с этим можем сумму расписать через сумму ряда образованного из простейших дробей, а дальше из разницы сумм рядов
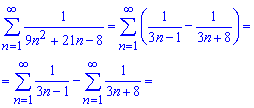
Далее расписываем каждый ряд в явную сумму и выделяем слагаемые (подчеркивание), которые превратятся 0 после сложения. Таким образом сумма ряда упростится к сумме 3 слагаемых (обозначены черным), что в результате даст 33/40.
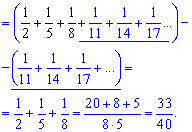
На этом базируется вся практическая часть нахождения суммы для простых рядов.
Примеры на сложные ряды сводятся к сумме бесконечно убывающих прогрессий и рядов, которые находят через соответствующие формулы, но здесь такие примеры рассматривать не будем.
б)
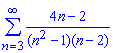
Вычисления: Находим границу n-го члена суммы
Она равна нулю, следовательно заданный ряд сходится и имеет смысл искать его сумму. Если граница отличная от нуля, то сумма ряда равна бесконечности со знаком "плюс" или "минус".
Найдем сумму ряда. Для этого общий член ряда который является дробью превратим методом неопределенных коэффициентов к сумме простых дробей I типа
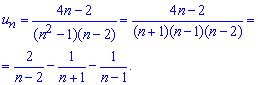
Далее по инструкции которая приводилась ранее записываем сумму ряда через соответствующие суммы простейших дробей
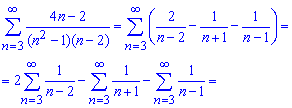
Расписываем суммы и выделяем слагаемые, которые станут равными 0 при суммировании.
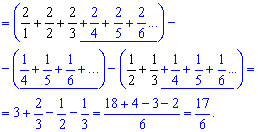
В результате получим сумму нескольких слагаемых (выделенные черным) которая равна 17/6.
Пример 1.9 Найти сумму ряда:
а) 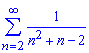
Вычисления: Вычислениям границы
![]()
убеждаемся что данный ряд сходится и можно находить сумму. Далее знаменатель функции от номера n раскладываем на простые множители, а весь дробь превращаем к сумме простых дробей I типа
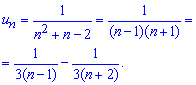
Далее сумму ряда в соответствии с расписанием записываем через два простые
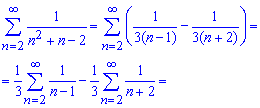
Ряды записываем в явном виде и выделяем слагаемые, которые после добавления дадут в сумме ноль. Остальные слагаемые (выделенные черным) и представляет собой конечную сумму ряда
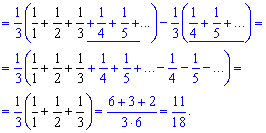
Таким образом, чтобы найти сумму ряда надо на практике свести под общий знаменатель 3 простых дроби.
б) 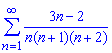
Вычисления: Граница члена ряда при больших значениях номера стремится к нулю
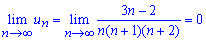
Из этого следует что ряд сходится, а его сумма конечна. Найдем сумму ряда, для этого сначала методом неопределенных коэффициентов разложим общий член ряда на три простейшего типа
![]()
Соответственно и сумму ряда можно превратить в сумму трех простых рядов
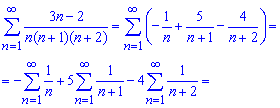
Далее ищем слагаемые во всех трех суммах, которые после суммирования превратятся в ноль. В рядах, содержащих три простых дроби один из них при суммировании становится равным нулю (выделен красным). Это служит своеобразной подсказкой в вычислениях
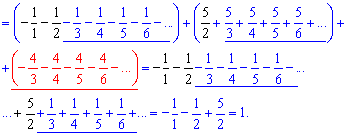
Сумма ряда равна сумме 3 слагаемых и равна единице.
Пример 1.15 Вычислить сумму ряда:
а) 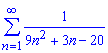
Вычисления: При общем член ряда стремящемся к нулю
![]()
данный ряд сходится. Преобразуем общий член таким образом, чтобы иметь сумму простейших дробей
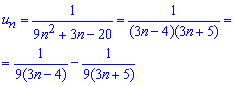
Далее заданный ряд, согласно формулам расписания, записываем через сумму двух рядов
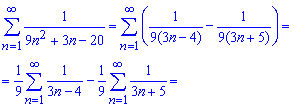
После записи в явном виде большинство членов ряда в результате суммирования станут равны нулю. Останется вычислить сумму трех слагаемых.
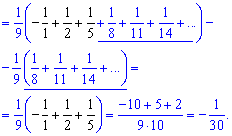
Сумма числового ряда равна -1/30.
б) 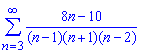
Вычисления: Поскольку граница общего члена ряда равна нулю,
![]()
то ряд сходится. Для нахождения суммы ряда разложим общий член на дроби простейшего типа.
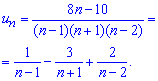
При разложении использовали метод неопределенных коэффициентов. Записываем сумму ряда из найденного расписание
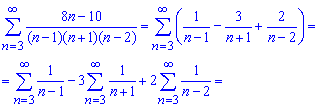
Следующим шагом выделяем слагаемые, не вносящие никакого вклада в конечную сумму и остальные оставшиеся
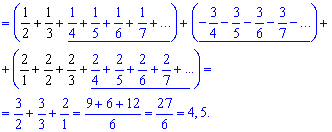
Сумма ряда равна 4,5.
Пример 1.25 Вычислить сумму рядов:
а) 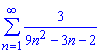
Вычисления: Находим границу общего члена ряда
![]()
Поскольку она равна нулю то ряд сходится. Можем найти сумму ряда. Для этого по схеме предыдущих примеров раскладываем общий член ряда через простейшие дроби
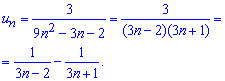
Это позволяет записать ряд через сумму простых рядов и, выделив в нем слагаемые, упростив при этом суммирование.
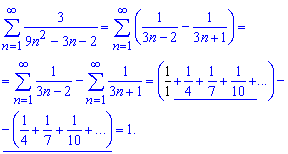
В этом случае останется одно слагаемое которое равен единице.
б) 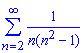
Вычисления: Находим границу общего члена ряда
![]()
и убеждаемся что ряд сходится. Далее общий член числового ряда методом неопределенных коэффициентов раскладываем на дроби простейшего типа.
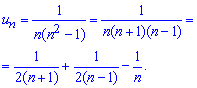
Через такие же дроби расписываем сумму ряда
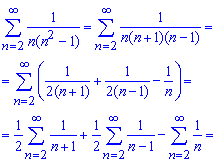
Записываем ряды в явном виде и упрощаем к сумме 3 слагаемых
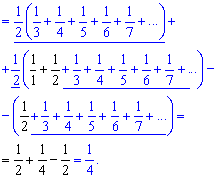
Сумма ряда равна 1/4.
На этом ознакомление со схемами суммирования рядов завершено. Здесь еще не рассмотрены ряды, которые сводятся к сумме бесконечно убывающей геометрической прогрессии, содержащие факториалы, степенные зависимости и подобные. Однако и приведенный материал будет полезен для студентов на контрольных и тестах.
Напомним что предпосылками для применения признака Даламбера служит наличие степенной зависимости (2, 3, a в степени n) или факториалов в формуле общего члена ряда. Будет это знаменатель или числитель дроби совсем не имеет значения, важно что имеем подобную зависимость, ну или факториал и степенную зависимость в одном наборе. С факториалами у многих на первых порах возникают проблемы но с практикой Вы заметете что ничего сложного в факториалах нет. Надо только расписать факториал подробно до тех пор когда в числителе или знаменателе дроби поучим одинаковые множителе. На словах это звучит не всем понятно, но следующие примеры помогут Вам в этом разобраться. Ну и самые сложные примеры предполагают наличие комбинаций факториалов и степенных зависимостей, два или более факториала, тоже и для степенной фунции, всевозможные цепочки множителей и другие каверзные комбинации. Ниже приведены базовые примеры с которых и начинается практика проверки сходимости ряда по Даламберу.
Пример: 2.5 Исследовать сходимость рядов
а) 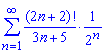
Вычисления: Поскольку данный ряд имеет положительные члены то исследовать его на сходимость можем с помощью признака Даламбера:
![]()
Если А<1 ряд сходящийся, А>1 - ряд расходящийся и при A=0 следует использовать другие признаки сходимости рядов.
Записываем общий член ряда и следующий, идущий после него
![]()
![]()
И находим границу их доли
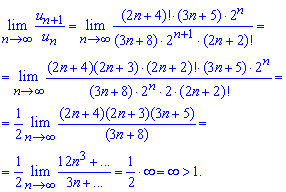
Поскольку граница бесконечна 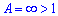 то по признаку Даламбера ряд расходящийся. Если искать суму ряда то она будет бесконечная.
то по признаку Даламбера ряд расходящийся. Если искать суму ряда то она будет бесконечная.
б) 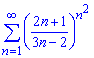
Вычисления: Члены ряда положительные поетому исследуем на сходимость по признаку Даламбера - записываем формулы последовательных членов ряда
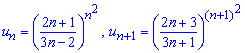
И находим предел отношения следующего члена к предыдущему при n стремящемуся к бесконечности
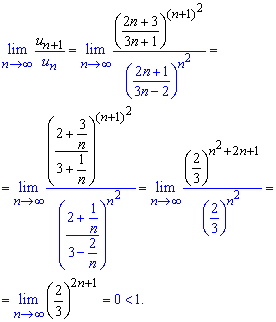
Граница равна нулю так как показатель стремится к бесконечности, а в скобках имеем значение меньше единицы.
По теореме Даламбера A = 0 <1 ряд сходится!
Пример: 2.8 Исследовать ряды на сходимость:
а) 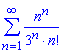
Вычисления: Как Вы уже убедились все примеры которые здесь рассматриваются следует проверять по признаку Даламбера.
В результате упрощения придем ко второму замечательному пределу - экспоненте
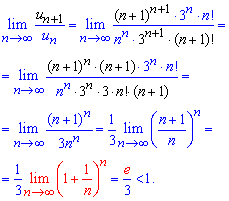
В общем граница меньше единицы ![]() следовательно ряд сходится.
следовательно ряд сходится.
б) 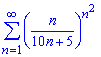
Вычисления: Для проверки на сходимость ряда по признаку Даламбера вычисляем предел
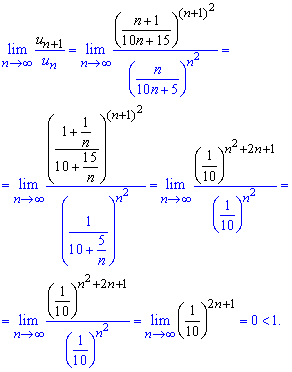
Предел равен 0 (A = 0 <1) следовательно ряд сходится!
Пример: 2.14 Исследовать ряд на сходимость
а) 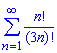
Вычисления: Находим предел следующего члена ряда к предыдущему
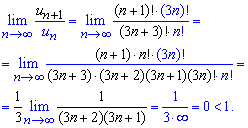
Для удобства чтения формул следующий член ряда выделенный в формулах черным цветом. Хорошо разберитесь как делить факториал на факториал, как показывает статистика множество неверных ответов Вы у Вас выходит в примерах с факториалами.
По признаку Даламбера ряд сходится.
б) 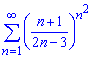
Вычисления: Записываем формулу общего члена ряда и последовавшего за ним
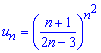
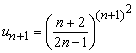
Подставляем их в формулу Даламбера и вычисляем предел
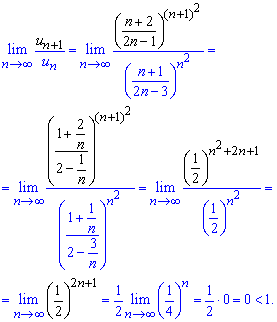
Граница равна нулю 0 <1, а это значит что данный ряд сходящийся.
Пример: 2.16 Исследовать ряд на сходимость:
а) 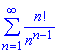
Вычисления: По признаку Даламбера проверяем границу общего члена ряда на ограниченность
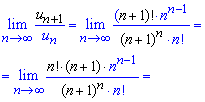
Превратив множители в числителе и знаменателе дроби сведем функцию в скобках ко второму замечательному пределу
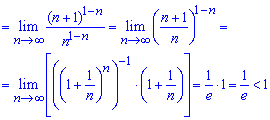
Поскольку граница меньше единицы
![]()
то согласно теореме Даламбера ряд сходящийся.
б) 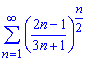
Вычисления: Задан числовой степенной ряд с положительными членами. Найдем предел отношения последующего члена ряда к предыдущему
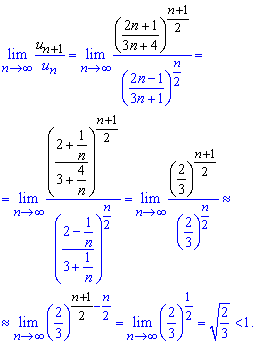
При исчислении границы считаю все моменты Вам понятны, если нет то Вам нужно прочесть статьи с категории "предел функций".
Получили предел меньше единицы,
![]()
следовательно ряд сходится за Даламбером .
Пример: 2.26 Исследовать сходимость ряда:
а) 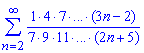
Вычисления: Для применения признака Даламбера выпишем общий член ряда и последующий за ним
![]()
![]()
Далее подставим их и найдем предел дроби
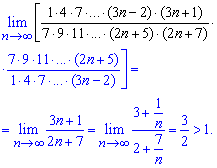
Предел равен A = 3/2> 1, а это значит что данный ряд расходящийся.
б) 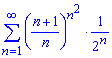
Вычисления: Записываем два последовательных члены положительного ряда
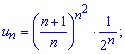
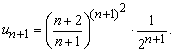
Находим границу для оценки сходимости ряда по теореме Даламбера.
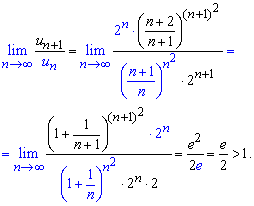
В ходе вычислений получим второй замечательный предел (экспоненту) как в числителе, так и в знаменателе. Результирующая граница больше единицы ![]() , следовательно делаем вывод о расхождении ряда.
, следовательно делаем вывод о расхождении ряда.
Пример: 3.6 Найти радиус сходимости и область сходимости степенных рядов:
а)
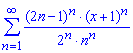
Вычисления: Для оценки сходимости ряда составим ряд с модулей членов заданного ряда, то есть ряд с последующим общим членом
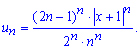
Далее, исходя с того что полученный ряд имеет положительные члены - исследовать его на сходимость будем с помощью признака Даламбера:
Для этого выписываем следующий после общего член ряда
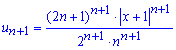
и подставляем в формулу предела. Вид членов ряда непрост, поэтому будьте внимательны при упрощении предела
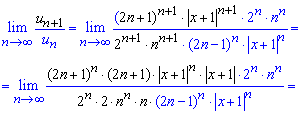
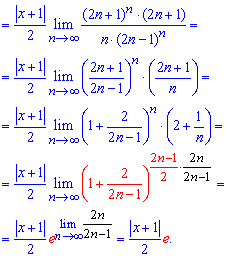
Наконец приходим к экспоненте и функциональному множителю.
Если граница меньше единицы
то ряд сходится по теореме Даламбера, причем абсолютно.
Отсюда составляем ограничения на допустимые "иксы"
Итак, ми нашли
Для себя запомните, что радиус сходимости функционального ряда равен половине расстояния между крайними точками области сходимости.
б)
Вычисления: Составим ряд из модулей членов заданного ряда, то есть с общим членом
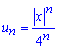
Нетрудно видеть что такой прием позволяет получить ряд с положительными членами и при этом исследовать его на сходимость с помощью признака Даламбера.
Для предела нам еще нужен следующий член ряда
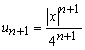
Подставляем члены ряда в предел и вычисляем
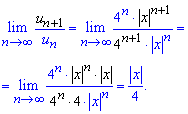
При пределе меньшей единицы
Из этого условия находим
В итоге мы нашли R=4 - радиус сходимости ряда и его область сходимости
Пример: 3.11 Найти радиус сходимости и область сходимости степенного ряда:
а)
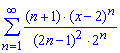
Вычисления: Члены заданного функционального ряда
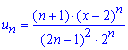
определены на всей действительной оси, то есть область определения следующая
Составляем ряд из модулей членов заданного ряда
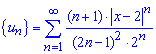
Его общий член может бить выражен формулой
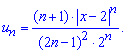
Поскольку новый ряд имеет положительные члены - исследуем на сходимость по Даламберу:
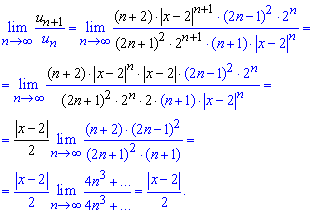
При
Отсюда находим R = 2 - радиус сходимости ряда и (0; 4) - область сходимости.
б)
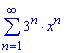
Вычисления: Члены заданного функционального ряда
![]()
определены для всех действительных переменных ![]() то есть область определения следующая
то есть область определения следующая
![]()
Составим ряд из модулей членов заданного ряда
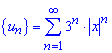
Снова применяем признак Даламбера для исследования ряда на сходимость
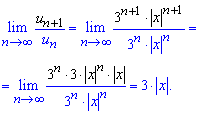
За Даламбером при пределе меньше единицы![]() - ряд убывает.
- ряд убывает.
Отсюда находим область сходимости
![]()
и R=1/3 радиус сходимости. Из приведенных примеров
Вы могли увидеть такую закономерность что значение которое ограничивает модуль с переменной и является радиусом сходимости ряда.
Область сходимости имеет в два раза большую длину и определяется раскрытием модуля.
Пример: 3.17 Найти радиус сходимости и область сходимости степенных рядов:
а) 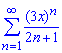
Вычисления: Члены функционального ряда
![]()
определены при 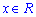 то есть
то есть ![]()
Составим ряд из модулей членов заданного ряда
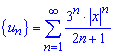
то есть
![]()
Исследуем его на сходимость по признаку Даламбера. Выписываем следующий после общего члена ряда
![]()
и подставляем в предел
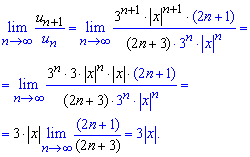
При 3|x|<1 - ряд убывает,
отсюда находим
![]() – область сходимости ряда.
– область сходимости ряда.
Все что находится справа от модуля это R = 1/3 - радиус сходимости ряда, а ограничения на "икс"
![]() – это область сходимости.
– это область сходимости.
б) 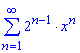
Вычисления: Члены функционального ряда
![]()
определены на всей действительной прямой ![]() , их область определения имеет вид
, их область определения имеет вид ![]() .
.
По схеме составляем ряд из модулей членов заданного ряда
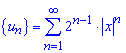
и получаем ряд со следующим общим членом
![]()
Образованный ряд будем анализировать на сходимость по признаку Даламбера
Выписываем следующий член ряда
![]()
и подставляем в предел
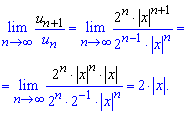
При 2|x|<1- ряд будет сходящимся.
Раскрываем модуль и находим
![]() - область сходимости и R=1/2 – радиус сходимости.
- область сходимости и R=1/2 – радиус сходимости.
В виде интервала записываем область сходимости ряда
![]()
Пример: 3.27 Найти радиус сходимости и область сходимости степенного ряда
а) 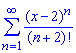
Вычисления: Члены функционального ряда 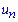 определены на действительной оси
определены на действительной оси ![]()
Сначала составим ряд из модулей членов этого ряда
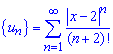
Общий член задается формулой
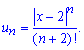
Исследуем ряд с модулей на сходимость по признаку Даламбера:
Находим предел отношения следующего члена ряда общему
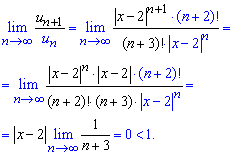
Поскольку A=0<1 то ряд сходится при всех действительных переменных, то есть имеет неограниченную ![]() - область сходимости.
- область сходимости.
Ряд имеет бесконечный ![]() радиус сходимости.
радиус сходимости.
б) 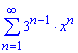
Вычисления: Члены ряда ![]() определены на множестве действительных чисел
определены на множестве действительных чисел
![]()
Построим ряд с модулей членов ряда:
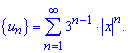
Далее записываем общий и следующий после него члены ряда
![]()
и подставляем в предел
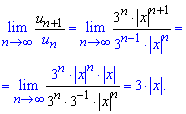
По теореме Даламбера ряд сходится при
3|x|<1. Из этого условия определяем
-![]() область сходимости ряда
область сходимости ряда
и R=1/3 – радиус сходимости.
В виде интервала записываем в ответ область сходимости ![]()
Теперь Вы знаете как найти область сходимости и радиус сходимости ряда. Пользуйтесь приведенными формулами и успешной Вам сдачи сессии.
Пример 4.7 Разложить функцию в ряд по степеням x
Вычисления: Выполняем разложение функции согласно формуле Маклорена. Сначала разложим в ряд знаменатель функции
напоследок умножим разложение на числитель.
Первое слагаемое - значение функции в нуле f (0) = 1/3.
Найдем производные функции первого и высших порядков f (x) и значение этих производных в точке x=0
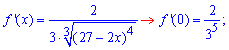
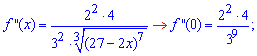
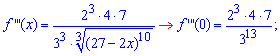
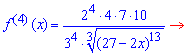
Далее с закономерности изменения значения производных в 0 записываем формулу для n-й производной
Итак, знаменатель представим в виде разложения в ряд Маклорена
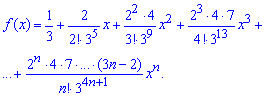
Умножаем на числитель и получаем искомое разложение функции в ряд по степеням х
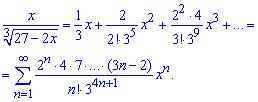
Как видите ничего сложного здесь нет.
Все ключевые моменты базируются на умении вычислять производные и быстрому обобщении значение производной старших порядков в нуле. Следующие примеры помогут Вам научиться быстро раскладывать функцию в ряд.
Пример 4.10 Найти разложение в ряд Маклорена функции
![]()
Вычисления: Как Вы возможно догадались раскладывать в ряд будем косинус в числителе. Для этого можете использовать формулы для бесконечно малых величин, или же вывести разложение косинуса через производные. В результате придем к следующему ряду по степеням x
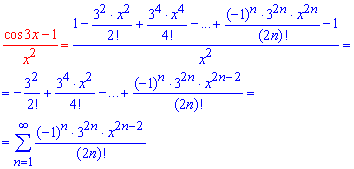
Как видите имеем минимум вычислений и компактную запись разложения в ряд.
Пример 4.16 Разложить функцию в ряд по степеням x:
7/(12-x-x^2)
Вычисления: В подобного рода примерах необходимо дробь разложить через сумму простейших дробей.
Как это делать мы сейчас не будем показывать, но с помощью неопределенных коэффициентов придем к сумме дох дробей.
Далее записываем знаменатели в показательной форме
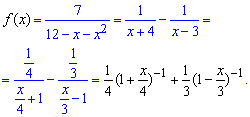
Осталось разложить слагаемые с помощью формулы Маклорена. Подытоживая слагаемые при одинаковых степенях "икс" составляем формулу общего члена разложения функции в ряд
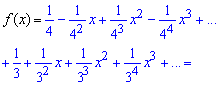
![]()
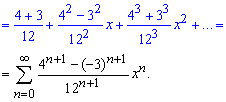
Последнюю часть перехода к ряду в начале трудно реализовать, поскольку сложно объединить формулы для парных и непарных индексов (степеней), но с практикой у Вас это будет получаться все лучше.
Пример 4.18 Найти разложение в ряд Маклорена функции
![]()
Вычисления: Найдем производную этой функции:
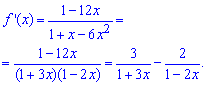
Разложим функцию ![]() в ряд, воспользовавшись одной из формул Макларена:
в ряд, воспользовавшись одной из формул Макларена:
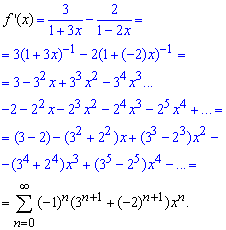
Ряды почленно суммируем на основе того, что оба абсолютно совпадающие. Проинтегрировав почленно весь ряд получим разложение функции в ряд по степеням x
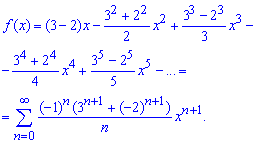
Между последними двумя строками разложения имеется переход который в начале у Вас будет забирать много времени. Обобщение формулы ряда не всем дается легко, поэтому не переживайте по поводу того что не можете достать красивой и компактной формулы.
Пример 4.28 Найти разложение в ряд Маклорена функции:
![]()
Запишем логарифм следующим образом
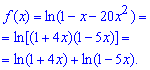
По формуле Маклорена раскладываем в ряд по степеням x логарифм функцию
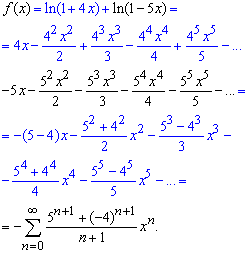
Конечное свертывания на первый взгляд сложное, однако при чередовании знаков Вы всегда получите нечто подобное. Входной урок по теме расписания функций в ряд завершено. Другие не менее интересные схемы разложения будут подробно рассмотрены в следующих материалах.
Пример 5.8 Разложить арктангенс в ряд по степеням x:
Вычисления: Напрямую раскладывать арктангенс я бы никому не советовал, поэтому сначала вычислим производную функции:
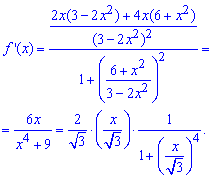
Обозначим за новую переменную
Далее знаменатель производной по формулам Макларена раскладываем в ряд
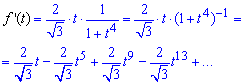
Возвращаясь к замене, получим разложение производной
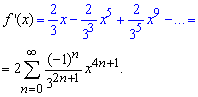
После этого почленно интегрируем весь ряд и получим конечную формулу разложения арктангенса
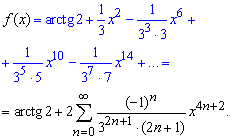
Вычислений много, но на практике задачи бывают не легче.
Пример 5.13 Найти разложение арктангенса в ряд по степеням x
Вычисляем производную от арктангенса, как от сложной функции
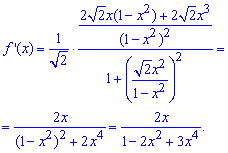
Упрощение позволяют получить компактный выражение производной Далее записываем расписание производной
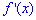 в ряд с неопределенными коэффициентами
в ряд с неопределенными коэффициентами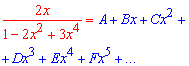
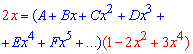
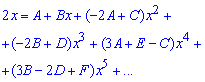
Полной схемы приводить сейчас не будем, однако если перенести знаменатель по правую сторону от знака равенства и приравнять коэффициенты при одинаковых степенях переменной x то получим разреженную систему уравнений и в конце ее решение:
A=0, B=2, C=0,D=4,E=0, F=2, ….
После этого можем записать разложение производной в виде
Если запись проинтегрировать, то получим расписание функции по степеням x
Формула несмотря на сложность расчетов, достаточно компактна.
Пример: 5.19 Найти разложение арксинуса в ряд по степеням x
Вычисления: По приведенной выше схеме сначала находим производную как от сложной функции:
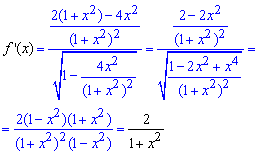
Раскладываем производную
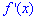 в ряд по формуле Маклорена
в ряд по формуле Маклорена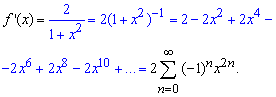
Интегрирования ряда не вызывает никаких проблем и мы получаем финальный расклад арксинуса в ряд
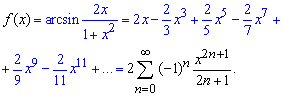
Пример: 5.29 Разложить логарифм в ряд по степеням x
Вычисления: Под логарифмом имеем сложную функцию, поэтому по правилу сначала дифференцируем логарифм, а затем умножаем на производную от функции в скобках
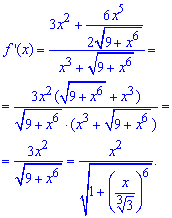
По формулам Маклорена раскладываем производную логарифма, а вернее ее знаменатель в ряд по степеням x
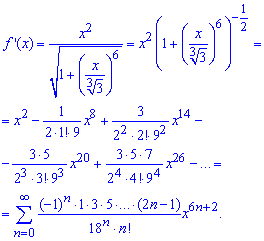
Общий член ряда содержит как показательную так и факториальную зависимость от индекса. Интегрируем члены ряда и, учитывая что f(0)=ln(3), получим разложение логарифма по степеням переменной x
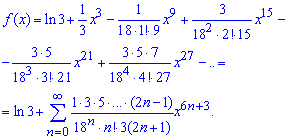
На этом знакомство с разложение функции в ряд Маклорена подходит к концу, больше примеров Вы найдете в следующих статьях.]]>
Задача: 1.3 Найти сумму ряда
а)
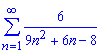
Решение: Сначала выполняем проверку ряда на сходимость
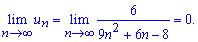
Граница общего члена ряда равна нулю, следовательно данный ряд сходится. Если Вы получите границу отличную от нуля, хотя и конечную то такой ряд будет расходящимся, а его сумма равна плюс или минус бесконечности. То есть такие ряды не убывают. На экзаменах, как правило, такие примеры не встречаются, однако на тестах возможно все. Поэтому прежде чем переходить к суммирования ряда проверяйте его на сходимость.
Напрямую Вы сумму этого ряда (из дробей) оценить не сможете, единственный выход разложить знаменатель общего члена ряда на простые множители, а дальше методом неопределенных коэффициентов сам дробь свести к разнице простых дробей
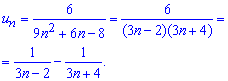
Это позволит свести вычисления суммы ряда к отысканию разности двух рядов
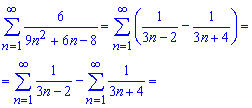
Если последние расписать в явном виде то всегда получите, что большинство слагаемых при исчислении даст ноль (подчеркнуты). Остальные оставшиеся (выделенные черным) и является искомой суммой ряда
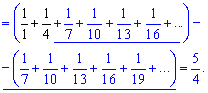
Теперь Вы на шаг ближе, чтобы самостоятельно найти сумму ряда.
б) вычислить сумму ряда
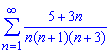
Решение: Нахождением границы
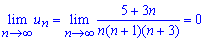
убеждаемся, что она равна 0, а заданный ряд сходящийся.
Далее методом неопределенных коэффициентов раскладываем общий член ряда на простые дроби
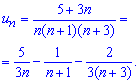
Это позволяет перейти от исчисления суммы одного сложного ряда к суммированию троих простых рядов
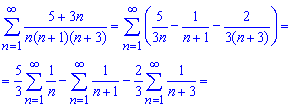
Ряды записываем в явном виде и выделяем слагаемые, которые взаимоуничтожаются при суммировании
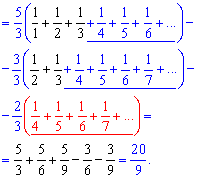
Подсказкой служит тот факт, что члены одного из рядов (выделен красным) в конечную сумму никакого вклада не внесут. Также для удобства вычислений записывайте ряды друг под другом. Для чего это нужно Вы можете видеть из этого примера.
Задача: 2.4 Исследовать сходимость рядов:
а) 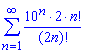
Решение:Заданный ряд имеет положительные члены, поэтому можем исследовать сходимость ряда по признаку Даламбера:
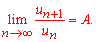
Записываем члены ряда, фигурирующие в пределе
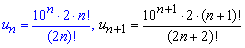
и подставляем в формулу Даламбера
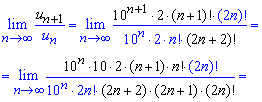
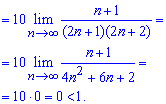
При исчислении предела большинство ошибок у студентов возникает при росписи факториалов, поэтому хорошо изучите свойства факториалов.
Поскольку предел меньше единицы A = 0 <1 то данный ряд сходящийся!
б) 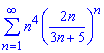
Решение:Исследовать на сходимость ряд будем по признаку Даламбера. Для этого записываем формулы общего члена ряда и последующего после него
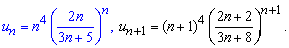
Далее подставляем их в предел и, насколько это возможно, упрощаем его
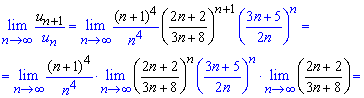
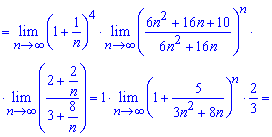
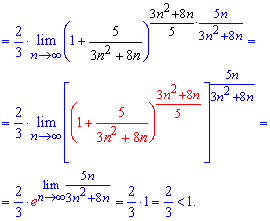
При исчислении один из множителей равен второму замечательному пределу - экспоненте.
Поскольку предел меньше единицы Lim=A = 2/3 <1 то делаем вывод о сходимости ряда.
Задача: 3.5 Найти радиус сходимости и область сходимости степенных рядов
а) 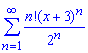
Решение: Заданный функциональный ряд может при определенных значениях переменной принимать отрицательные значения, поэтому для исследования сходимости ряда по признаку Даламбера
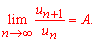
составим ряд с модулей членов заданного ряда
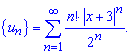
Записываем общий и следующий после него члены ряда из модулей
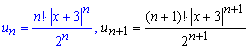
и подставляем их в предел
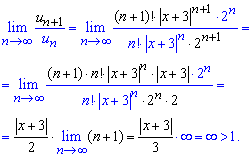
Расписав факториалы и степенные зависимости придем к зависимости которая не ограничена. Предел равен бесконечности, следовательно функциональный ряд расходится (по теореме Даламбера) при всех действительных значениях переменной 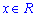 .
.
Это означает что радиус сходимости равен нулю R = 0, а область сходимости пустое множество 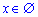 .
.
б) 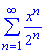
Решение: Составим ряд из модулей членов заданного ряда:
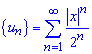 ,
,
а дальше выполняем исследования ряда на сходимость по теореме Даламбера.
Находим предел доли старшего к младшему члену функционального ряда
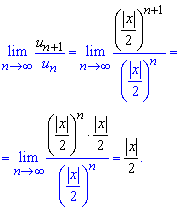
Согласно теореме Даламбера ряд совпадает для переменных, которые удовлетворяют условие
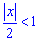 .
.
Раскрывая модуль находим 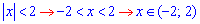 область сходимости ряда и записываем радиус сходимости R=2.
область сходимости ряда и записываем радиус сходимости R=2.
Задача: 4.6 Найти разложение дробной функции в ряд по степеням x:
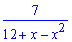
Решение: Разложим функцию методом неопределенных коэффициентов на сумму простых дробей, а дальше превратим знаменатели, чтобы иметь удобный запись для расписания
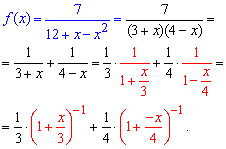
Функцию f(x) разложим в ряд по степеням x воспользовавшись формулами Маклорена для степенных функций:
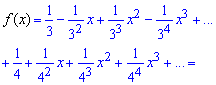
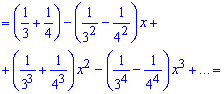
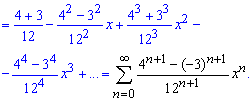
В конце группируем слагаемые при одинаковых степенях "икс" и записываем разложение функции одним рядом.
Задача: 5.7 Найти разложение арктангенса в ряд по степеням x:
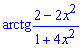
Решение: Для расписания арктангенса применим следующую методику. Сначала найдем производную сложной функции от арктангенса
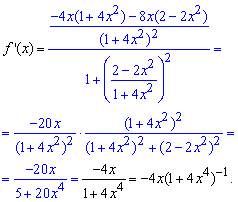
Разложим производную арктангенса в ряд по степеням x, используя формулы Маклорена
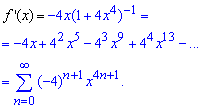
Чтобы получить разложение арктангенса в ряд интегрируем производную. Учитывая что f(0)=arctg(2), получим ряд по степеням x заданной функции f(x):
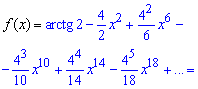
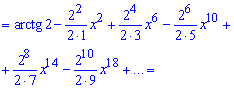
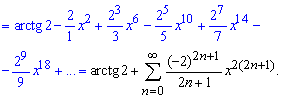
Последний переход к ряду не так очевиден, однако для знакопеременного ряда именно такие зависимости получают в ответах.
Задача: 6.8 Разложить функцию в тригонометрический ряд Фурье:
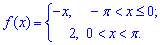
Схема разложения в ряд Фурье подробно расписана в предыдущих статьях. Здесь интегрированием определяем коэффициенты Фурье
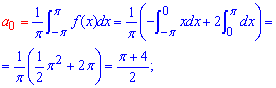
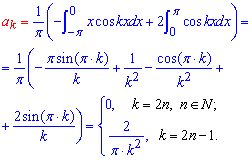
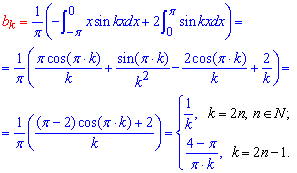
Далее согласно формулам для заданной функции составляем разложение в ряд Фурье
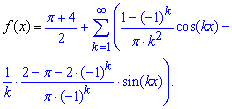
В конечном раскладе функции коэффициенты Фурье для нечетных и четных индексов объединили в один. В этом, как и в интегрировании вся сложность разложения функции в тригонометрический ряд. Вот такие задачи по теории рядов Вам придется решать на контрольной или экзаменах. Если сомневаетесь в собственных силах, то мы поможем Вам сдать сессию.
Разложение кусковой функции в ряд Фурье находят по формуле
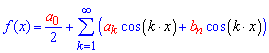
где коэффициенты Фурье вычисляют интегрированием
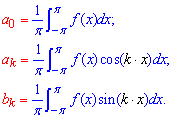
Таким образом, чтобы разложить функцию в ряд Фурье на практике необходимо всего лишь найти коэффициенты Фурье, а для этого нужно хорошо уметь интегрировать. На деле это занимает много времени и сил и многим бывает не под силу. В этом Вы сейчас наглядно убедитесь.
Пример: 6.9 Разложить функцию в тригонометрический ряд Фурье:
Вычисления: Заданная функция непереодическая. Для вычисления коэффициентов Фурье используем формулы
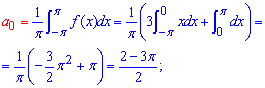
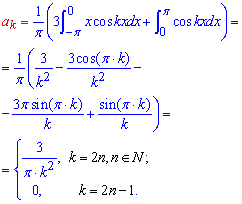
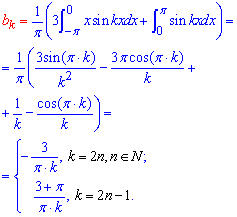
Сложность заключается в том, что для конечной формулы разложения ряда коэффициенты Фурье с четными и нечетными индексами надо свести в один.
Это требует определенных умений, однако реализовать это может научиться каждый. Кроме того, Вы должны безупречно знать что sin(0)=sin(Pi)=0, cos(0)=1, cos(Pi)=-1.
После всех манипуляций разложение функции в ряд Фурье должно принять вид
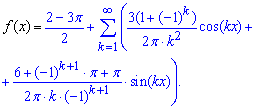
Если в результате вычислений Вы получили что-то отменное от этого, значит Вы где-то допустили ошибку.
Пример: 6.12 Найти разложение функции в тригонометрический ряд Фурье
Вычисления: Интегрированием функции с тригонометрическими множителями и без них находим коэффициенты Фурье
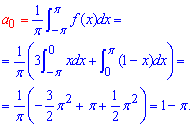
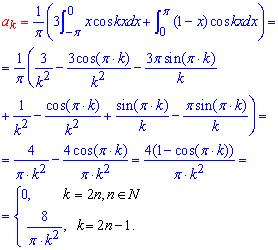
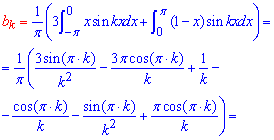
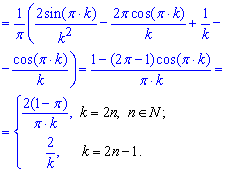
Составляем формулы коэффициентов Фурье и записываем разложение функции в тригонометрический ряд
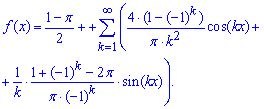
Пример: 6.18 Найти разложение функции в тригонометрический ряд Фурье:
Вычисления: Находим коэффициенты Фурье интегрированием
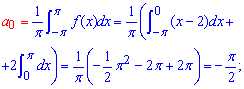
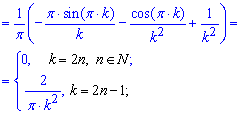
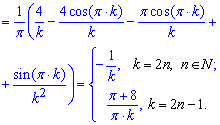
Интегралы по силам каждому, для вычисления меж необходимы лишь знания значений синуса и косинуса в -Pi 0, Pi. Подставляем полученные коэффициенты в ряд Фурье и получаем следующее разложение функции
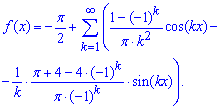
Пример: 6.20 Найти разложение функции в тригонометрический ряд Фурье:
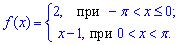
Вычисления: Интегрированием находим коэффициенты Фурье a0, ak, bk
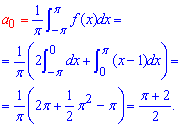
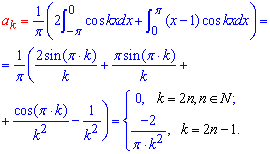
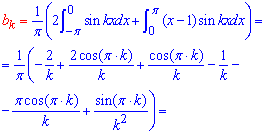
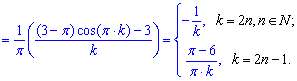
Далее для коэффициентов составляем общие формулы и подставляем в формулу разложения функции в тригонометрический ряд Фурье
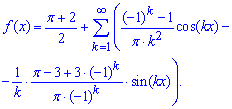
Пример 6.30 Разложить функцию в тригонометрический ряд Фурье:
![]()
Вычисления: Определим интегрированием коэффициенты Фурье:
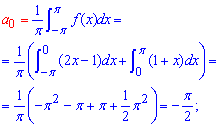
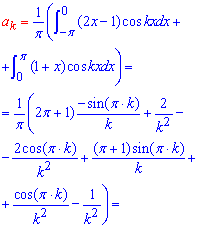
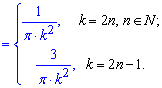
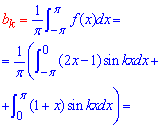
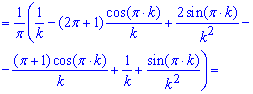
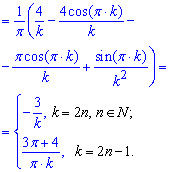
Вычисления достаточно громоздки, поэтому хорошо разберите формулы и для себя изучите методику интегрирования.
При сворачивании коэффициентов Фурье получим искомое разложение функции в ряд Фурье
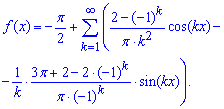
Как Вы могли убедиться разложить функцию в ряд Фурье по силам не каждому студенту. Умение интегрировать и знания рядов Вам в этом будут хорошими помощниками.
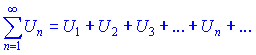
называется положительным, если все его члены неотрицательные
![]()
Для определения сходимости в литературе собраны правила которые позволяют это быстро определить. Рассмотрим по очереди признаки сходимости числовых рядов
Признак сравнения
Рассмотрим два ряда с положительными членами
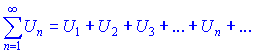
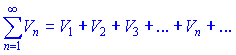
Для них выполняются следующие утверждения:
1. Если члены ряда ![]() не больше соответствующих членов
не больше соответствующих членов ![]() сходящегося ряда
сходящегося ряда ![]() (
(![]() ) то ряд
) то ряд ![]() сходится.
сходится.
Если каждый член ряда ![]() больше (или ровный) соответствующего члена росходящегося ряда
больше (или ровный) соответствующего члена росходящегося ряда ![]() то ряд
то ряд ![]() разбегается.
разбегается.
--------------------------------------------
Пример 1.
Исследовать на сходимость ряды
1) 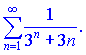
2) 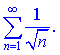
Решение.
1) Сравним заданный ряд
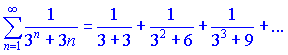
с рядом геометрической прогрессии знаменатель которой равен ![]()
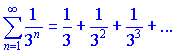
Каждый член первого ряда меньше соответствующего член ряда геометрической прогрессии, который сбегается, поскольку
![]()
![]()
По признаку сравнения первый ряд сходится.
2) Члена данного ряда сравниваем с соответствующими гармонического ряда. Для произвольного ![]() выполняется неравенство
выполняется неравенство
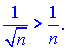
Так как гармонический ряд разбежный то в соответствии с признаком сравнения заданный ряд также разбежный.
--------------------------------------------
Предельный признак сравнения
Пусть ряды ![]() и
и ![]() положительные, а также существует предельная граница
положительные, а также существует предельная граница
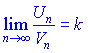
причем ![]() , тогда оба ряда или одновременно совпадающие или одновременно разбежные.
, тогда оба ряда или одновременно совпадающие или одновременно разбежные.
--------------------------------------------
Пример 2.
Исследовать на сходимость ряд
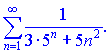
Решение.
Для сравнения выберем ряд ![]() совпадающей геометрической прогрессии. Применяя предельный признак будем иметь
совпадающей геометрической прогрессии. Применяя предельный признак будем иметь
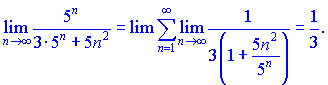
Поскольку оба ряды ведут себя равносильно ![]() , а геометрический ряд сходится, то и рассмотренный ряд также сходится.
, а геометрический ряд сходится, то и рассмотренный ряд также сходится.
--------------------------------------------
Признак Даламбера
Пусть члены ряда
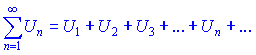
положительные и отношение ![]() -го члена до
-го члена до ![]() -го имеет предел при
-го имеет предел при![]()
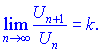
Если![]() то ряд сходится,
то ряд сходится,
если ![]() - ряд расходится.
- ряд расходится.
При ![]() надо применять другой признак сходимости, поскольку данный признак не может определить сходится ряд или расходится.
надо применять другой признак сходимости, поскольку данный признак не может определить сходится ряд или расходится.
--------------------------------------------
Пример 3.
Исследовать на сходимость ряды
1) 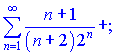
2) 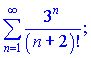
3) 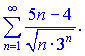
Решение.
1) Найдем границу отношения ![]() члена до
члена до ![]() -го при
-го при ![]()
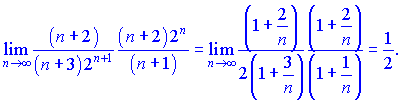
Поскольку ![]() то ряд сходится.
то ряд сходится.
2) Вычислим границу
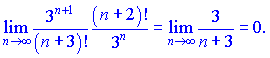
Ряд сходящийся, так как ![]()
3) Применим признак Даламбера
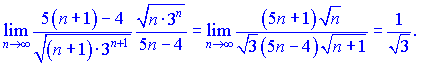
Видим что ряд сходящийся поскольку![]()
------------------------------------------
Радикальный признак Коши
Если для ряда ![]() положительными членами существует граница
положительными членами существует граница
![]()
то при ![]() ряд сходится, а при
ряд сходится, а при ![]() - разбегається.
- разбегається.
При ![]() нужно применять другой признак сходимости.
нужно применять другой признак сходимости.
-------------------------------------------
Пример 4.
Исследовать на сходимость ряды
1) 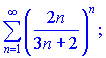
2) 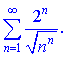
Решение.
1) Применим признак Коши
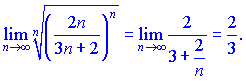
Ряд совпадающий поскольку![]()
2) Вычислим границу
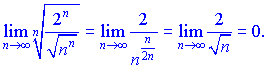
Данный ряд также совпадающий, поскольку ![]()
--------------------------------------------
Интегральный признак Коши
Пусть задан ряд
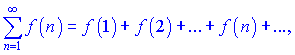
причем функция![]() положительная, непрерывная и монотонно нисходящая функция от переменной
положительная, непрерывная и монотонно нисходящая функция от переменной ![]() . Тогда
. Тогда
1) ряд 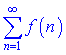 совпадающий, если несвойственный интеграл
совпадающий, если несвойственный интеграл
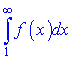
совпадающий;
2) ряд разбежный когда интеграл разбежный.
Под сходимостью интегралу следует понимать его ограниченность, то есть
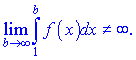
Рассмотрим примеры применения интегрального признака Коши.
--------------------------------------------
Пример 5.
Исследовать на сходимость
1) 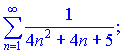
2) 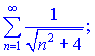
3) 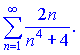
Решение.
1) Применим интегральный признак Коши
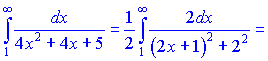
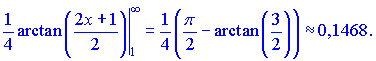
Ряд совпадающий поскольку интеграл совпадающий.
2) Найдем интеграл
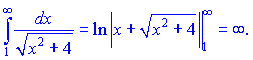
По интегральному признаку Коши ряд разбежный.
3) Вычислим интеграл
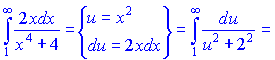
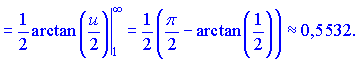
Данный ряд совпадающий.
----------------------------------------------
------------------------------
]]>