Задачи на сложные проценты решаются в достаточно быстрый способ при знании нескольких простых формул. Часть из них касается начислений по вкладу или кредиту, когда те осуществляются через определенные промежутки времени . Также сложные проценты используют в задачах химии, медицины и ряде других сфер.
ФОРМУЛЫ СЛОЖНЫХ ПРОЦЕНТОВ
В случае размещения вкладов с капитализацией процентов на годы конечная сумма депозита определяется формулой
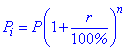Здесь P – первоначальный взнос, r – процентная ставка, n – количество лет. По сложным процентам работают банки, инвестиционные фонды, страховые компании. Распространенные за рубежом, а теперь и в Украине - пенсионные фонды и фонды страхования жизни работают по схеме сложных процентов.
При размещении вкладов с капитализацией процентов ежеквартально формула сложных процентов будет выглядеть
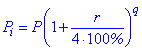где q – количество полных кварталов.
При капитализации процентов ежемесячно применяют следующую формулу для вычислений
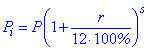где s – количество месяцев существования соглашения.
Последний случай, непрерывное начисление процентов, когда сложные проценты начисляются ежедневно, рассчитывают по формуле
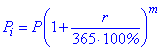где m – количество дней.
Страхование жизни и откладывания пенсий исчисляют сложными формулами, кроме начисления сложных процентов ежегодно осуществляются необходимые взносы.
Рассмотрим два случая накопления. Мужчина откладывает 5000 грн. в течение 20 лет. За это время он отложит
20*5000=100000 (грн).
При откладывании в накопительные фонды с годовой ставкой 13%, за первый год сумма возрастет до
5000*(1+13/100)=5650 (грн).
В следующем году человек в данной суммы добавляет еще 5000 грн. В результате, за второй год сумма увеличится
(5650+5000)*(1+0,13)=12034.50 (грн) .
Продолжая подобные вычисления, в конце срока получим сумму размером 457349,58 грн.
Поверьте - ошибок при исчислении форуме, большое значение набегает за счет сложных процентов. Сомнительным остается только история изменения платежеспособности гривны через 20 лет. Учитывая политику государства вкладывать деньги в такие фонды люди не спешат, однако за рубежом практика откладывания денег распространена, правда процентные ставки намного ниже.
Рассмотрим распространенные задачи на сложные проценты.
Пример 1. Вкладчик положил на депозит $ 3000 под 9% годовых на 10 лет. Какая сумма аккумулируется конце 10-го года при годовой капитализации? На сколько вырастет сумма по сравнению с первоначальным взносом?
Решение: Применяем формулу сложных процентов для нахождения суммы в конце срока
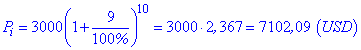
Чтобы ответить на второй вопрос, от значения 7102,09 вычитаем сумму вклада.
Разница составляет 4102 доллара.
Пример 2. Инвестор вложил 7000 грн под 10% годовых при условии начисления сложных процентов ежеквартально. Какую сумму он получит через 8 лет?
Решение: Применяем 2 формулу сложных процентов. Находим количество кварталов
8*4=32.
и подставляем в формулу
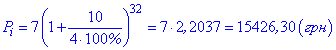
Школьные задачи на сложные проценты
Например, возьмем задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир «Аглгебра». (Номер в скобках)
Задача 1. (556) Костюм стоил 600 грн. После того как цена была снижена дважды, он стал стоить 432 грн., Причем процент снижения второй был в 2 раза больше, чем в первый раз. На сколько процентов каждый раз снижалась цена?
Решение: Для упрощения вычислений обозначим
X – первая скидка;
X/2 – вторая скидка.
Для вычисления неизвестной X составляем уравнение
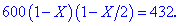
Упрощаем, и сводим к квадратному уравнению
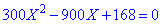
и решаем
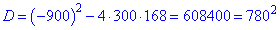
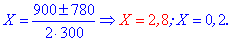
Первый решение не имеет физического смысла, второй учитываем при вычислениях. Значение 0,2 соответствует снижению на 0,2*100%=20% после первой скидки, и X/2 =10% после второй скидки.
Задача 2. (557) Определенный товар стоил 200 грн. Сначала его цену повысили на несколько процентов, а затем снизили на столько же процентов, после чего стоимость его стала 192 грн. На сколько процентов каждый раз происходила смена цены товара?
Решение: Поскольку проценты одинаковы, то обозначаем изменении цены товара через X.
На основе условия задачи получим уравнение
Его упрощение приведет к решению уравнения
откуда корни приобретут значений
Первая значение отвергаем, оно меняет суть задачи (сначала имеем снижение, а затем рост процентов, противоречит условию). Второе при пересчете составит 0,2*100%=20% процентов.
Задача 3. (558) Вкладчик положил в банк 4000 грн. За первый год ему начислена определенный процент годовых, а второго года банковский процент увеличен на 4%. На конец второго года на счете стало 4664 грн. Сколько процентов составила банковская ставка в первый год?
Решение: Обозначим через X – увеличение вклада в первый год, тогда
X+4/100%=X+0,04
начисления во второй год.
По условию задачи составляем уравнение для определения неизвестной X
После упрощений получим квадратное уравнение вида
Вычисляем дискриминант
и корни уравнения
Первый корень отбрасываем, второй соответствует ставке в 6% годовых.
Задача 4. (564) В сосуде 12 кг кислоты. Часть кислоты отлили и долили до прежнего уровня водой. Затем снова отлили столько же, как и в первый раз, и долили водой до прежнего уровня. Сколько литров жидкости отливали каждый раз, если в результате получили 25-процентный раствор кислоты?
Решение: Обозначим через X – часть кислоты, которую отливали.
После первого раза ее осталось 12-X, а процентное содержание кислоты
После второй попытки содержание кислоты в сосуде составило
.
Разведя водой до 12 кг, процентное содержание составляло 25%. Составляем уравнение
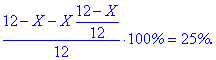
Упрощаем проценты и избавляемся знаменателей
Решаем квадратное уравнение
Условии задачи удовлетворяет второе решение, а это значит, что каждый раз отливали 6 кг жидкости.
На этом знакомство со сложными процентами завершается. На практике Вам встретятся как простые так и сложные задачи. При проблемах с вычисления сложных процентов обращайтесь к нам, мы поможем Вам в решении задач.
