logaf(x)=c⇔f(x)=ac.
{x>0, x≠1, f(x)>0}
и ее частичными случаями:
логарифм основания равен единице
c=1⇔logaa=1⇔f(x)=a.
логарифм единицы равен нулю
c=1⇔loga1=0⇔f(x)=1.
Мы настолько часто пользуемся этими свойствами логарифмов, что после прочтения всех примеров Вы точно будете знать, где и для чего нужны эти формулы.
Примеры раскрытия логарифмических уравнений
Курс подготовки ВНО состоит из 40 примеров от простых до сложных, так что по номеру примера Вы можете следить, какой класс задач решается. По мере углубления Вы будете знакомиться с новыми формулами и свойствами логарифмов, без которых уравнение невозможно решить.
Пример 16.7 Решить уравнение log2(x+1)-log2(x-1)=1 и указать промежуток, которому принадлежит его корень.
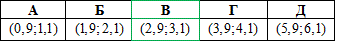
Решение: Выписываем ОДЗ:
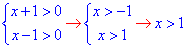
По правилу, разницу логарифмов выражений заменяем логарифмом частки + логарифм основания равен единице, в результате опускаем логарифмы и приравниваем выражения:
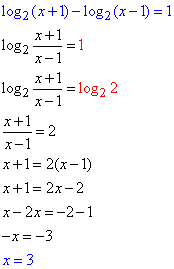
x=3 – корень заданного уравнения, принадлежащий промежутку (2,9;3,1).
Ответ: (2,9;3,1) – В.
Пример 16.8 Решить уравнение log2(x+1)+log(x+2)=3-log24 и указать промежуток, которому принадлежит его корень.
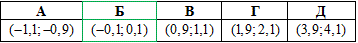
Решение: Составим систему неравенств для ОДЗ:
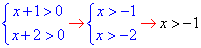
Используя ряд свойств логарифма, сводим уравнение к одному основанию, и раскрываем его.
Далее раскладываем неполное квадратное уравнение на простые множители
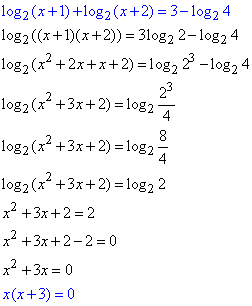
x1=0
x2=-3<-1 (не принадлежит ОДЗ).
x=0 – единственный корень заданного уравнения с интервала (-0,1;0,1).
Ответ: (-0,1;0,1) – Б.
Пример 16.10 Указать уравнение, равносильное уравнению
log3x-log9x+log81x=7.
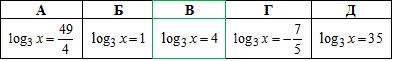
Решение: ОДЗ: x>0
Вынесем степени из основания логарифмов и сгруппируем
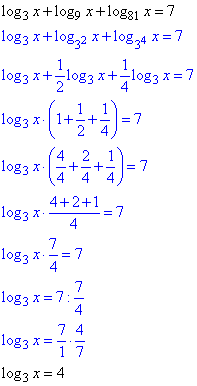
Уравнение log3x=4 и есть равносильное заданному.
(его решение x=3^4=81).
Ответ: log3x=4 – У.
Пример 16.11 Указать уравнение, равносильное уравнению x^lg(x)=10.
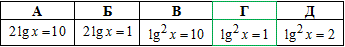
Решение: ОДЗ: {x>0, x≠1}.
Прологарифмируем обе части показательного уравнения
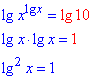
Конечное уравнение и является искомым равносильным уравнением.
(x1=10 или x2=0,1).
Ответ: lg2x=1 – Г.
Пример 16.12 Указать уравнение, которое получается из уравнения x^lg(x)=1000x^2 в результате логарифмирования обеих его частей.
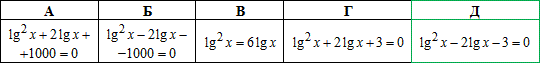
Решение: ОДЗ: {x>0, x≠1}.
Прологарифмируем обе части уравнения по основанию 10.
При этом помните, что десятичный логарифм 10 равен 1
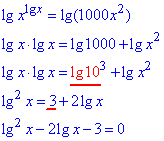
таким образом нашли уравнение, которое равносильно начальному.
(x1=1000 или x2=0,1).
Ответ: lg2(x)-2•lg(x)-3=0 – Д.
Пример 16.13 Указать уравнение, равносильное уравнению 2lgx2-lg2(-x)=4.
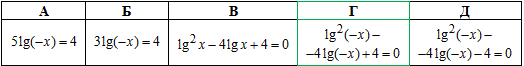
Решение: ОДЗ: -x>0, x<0.
Вынесем из под логарифма степень =2 и перегруппируем слагаемые
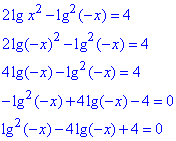
Это и есть все манипуляции, чтобы найти уравнение, которое равносильно заданному
2lgx2-lg2(-x)=4.
С помощью других преобразований Вы бы его не получили.
(x=-100).
Ответ: lg2(-x)-4•lg(-x)+4=0 – Г.
Пример 16.14 Решить уравнения
logalogblogcx=0.
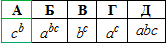
Решение: ОДЗ: x>0.
Имеем три вложенные логарифмы, поэтому по свойствам добиваемся равных основ логарифмов справа и слева от знака равенства, и раскрываем уравнение за схемой
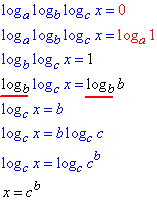
Такого плана задания в свое время были популярны на олимпиадах.
Ответ: cb – А.
Пример 16.15 Указать количество корней уравнения
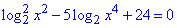
|
А |
Б |
В |
Г |
Д |
|
Четыре |
три |
два |
один |
ни одного |
Решение: ОДЗ: x≠0.
Путем введения замены переменных уравнение сводим к квадратному, после вычисления которого решаем 2 простых логарифмических уравнения.
Подробные объяснения хода преобразований приведены в таблице

Все найденные значения (-8; -4; 4; 8) принадлежат ОДЗ, уравнение имеет четыре решения.
Ответ: Четыре – А.
Пример 16.24 Установить соответствие между уравнениями (1-4) и произведениями их корней (А–Д).
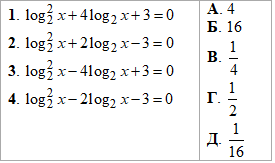
Решение: Все 4 варианта логарифмических уравнений сводим путем замены переменных к квадратным, после нахождения корней последних возвращаемся к замене и вычисляем простые уравнения с логарифмами. Так как в ответе нужно найти произведение корней, то условие ОДЗ допускает все значения.
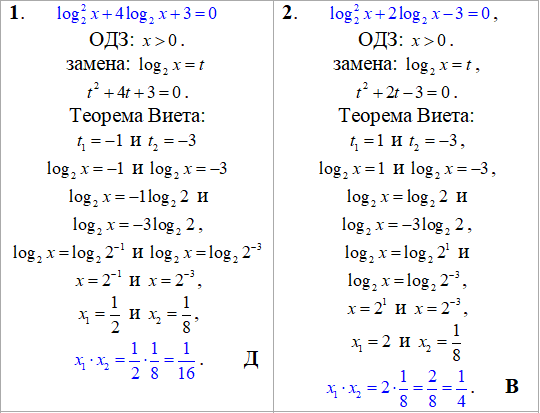

Решение уравнений с логарифмами невозможно без знания их свойств. Обращайте внимание на подчеркивания в формулах, они даются не просто так, эти две формулы к концу занятий Вы должны выучить на память и поверьте, что у Вас это получится.
А сейчас переходите к новым готовым ответам с ВНО подготовки на логарифмические уравнения.
При равносильных преобразованиях справедливая формула перехода от логарифмического до простого уравнения
logaf(x)=c⇔f(x)=ac.
ОДЗ: основание логарифма должно быть больше нуля и не равняться единице,
функция – положительной
{x>0, x≠1, f(x)>0}.
Важно знать частные случаи простейших логарифмических уравнений:
правая сторjна равна нулю (с=0) или единицы (с=1):
логарифм основания равен единице
c=1⇔logaa=1⇔f(x)=a.
логарифм единицы равен нулю
c=1⇔loga1=0⇔f(x)=1.
Эти формулы Вы должны знать на память, поскольку их чаще всего применяют при сведении логарифмов до простейшего типа.
С целью научить Вас раскрывать логарифмические уравнения, а также подготовить к ВНО тестированию нами решены 40 примеров, которые в полной мере охватывают все известные методы решения логарифмических уравнений, которые Вас учат в 10-11 классе школьной программы, и дальше на первых курсах в ВУЗ-ах.
Схема вычисления логарифмических уравнений
- если возможно, выписать область допустимых значений логарифмов и функций, которые в него входят.
- свести уравнение к простейшему типу путем элементарных преобразований, которые заключаются в вынесении степени из основания логарифма (или наоборот), логарифмированию и потенцированию (возведение в степень по основанию (экспонента, основы =10, 2, π)
- в случаях сложных уравнений вводят замену переменных и сводят к квадратным или другим известным уравнениям.
Вычисление уравнений с логарифмом
Пример 16.1 Решить уравнение logax=c.
|
А |
Б |
В |
Г |
Д |
|
ø |
a•c |
ca |
ac |
c/a |
Решение: Имеем простейшее логарифмическое уравнение, которое решается методом сведения к одному основанию логарифмов:
logax=c
(здесь a>0, a≠1),
logax=c•1,
logax=c•logaa,
logax= logaac
Здесь использовали свойства логарифма, единицу расписали как логарифм основания, после чего множитель c внесли под логарифм.
Далее опустили основы и приравняли выражения в логарифмах:
x=ac.
ОДЗ: x>0.
Ответ: ac – Г.
Пример 16.2 Решить уравнение log1/2(x)=-4.
|
А |
Б |
В |
Г |
Д |
|
ø |
-16 |
1/16 |
1/16; 16 |
16 |
Решение: ОДЗ функции под логарифмом: x>0.
Сводим уравнение к одному основанию логарифмов
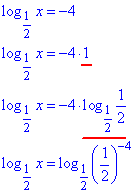
При равных основах приравниваем выражения под логарифмами:
x=(1/2)-4,
x=24,
x=16.
Ответ: 16 – Д.
Пример 16.3 Решить уравнение log2(-x)=5.
|
А |
Б |
В |
Г |
Д |
|
ø |
32 |
-32 |
1/32 |
-1/32 |
Решение: Выполняем раскрытия логарифмов по данной в начале инструкции:
ОДЗ – -x>0,x<0.
Упростим уравнения
log2(-x)=5
log2(-x)=5•1
log2(-x)=5• log22
log2(-x)= log225
опустим основы и приравняем логарифмические выражения:
-x=25,
-x=32,
x=-32.
Ответ: -32 – У.
Пример 16.4 Решить уравнение lg(x2-x)=1-lg(5).
|
А |
Б |
В |
Г |
Д |
|
ø |
-3; 2 |
-2; 1 |
-2; 3 |
-1; 2 |
Решение: ОДЗ: x2-x>0,
x(x-1)>0
Решим неравенство методом интервалов
x(x-1)=0,
x1=0,
x2=1.

x∈(-∞;1)∪(1;+∞).
На этом множестве значений и ищем решение уравнения, сперва сведя к одной основе логарифмы
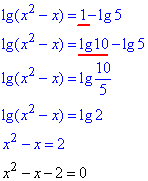
по теореме Виета:
x1+x2=1,
x1•x2=-2.
x1=-1,
x2=2.
Оба корня принадлежат ОДЗ.
Ответ: -1; 2 – Д.
ОДЗ неравенства могут быть сложнее, чем сами уравнения, тогда достаточно сами корни уравнения подставить в неравенство (или систему неравенств) и определить, принадлежат ли корни области допустимых значений логарифмческого уравнения.
Пример 16.5 Сколько корней имеет уравнение lg(x4-10x2)=lg3x3?
|
А |
Б |
В |
Г |
Д |
|
Ни одного |
один |
два |
три |
четыре |
Решение: В логарифме имеем биквадратное выражение, которое при условиях на ОДЗ требует вычислений.
Поэтому пойдем другим путем, сначала решим уравнение с логарифмом, а в конце проверим удовлетворяют ли найденные "иксы" ОДЗ:
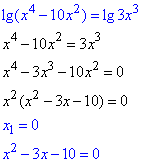
по теореме Виета:
x2+x3=3
x2•x3=-10.
x2=-2
x3=5.
Проверим найденные значения 0; -2; 5 являются решениями.
Выписываем ОДЗ и подставляем "иксы":
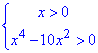
1) 0=0, поэтому x1=0 не принадлежит ОДЗ;
2) (-2)4-10•(-2)=16-40=-24<0
x2=-2 не принадлежит ОДЗ.
3) 5^4-10•5^2=625-250=375>0,
x3=5 удовлетворяет ОДЗ.
Логарифмическое уравнение lg(x^4-10x^2)=lg3x3 имеет один корень.
Ответ: один – Б.
Пример 16.6 Решить уравнение log6(x-2)+log6(x-1)=1 и указать промежуток, которому принадлежит его корень.
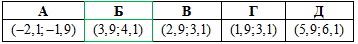
Решение: Выпишем систему неровностей для ОДЗ:
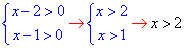
По правилу, что сумма логарифмов чисел равна логарифму их произведения ln(a)+ln(b)=ln(a•b) и свойству log66=1, сведем логарифмы к общему основанию:
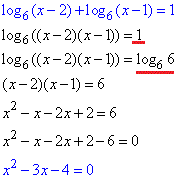
При преобразованиях получили квадратное уравнение, корни которого находим по теореме Виета:
x1+x2=3
x1•x2=-4.
x1=-1<2 (не принадлежит ОДЗ)
x2=4.
x=4 – единственный корень заданного уравнения, он принадлежит промежутку (3,9;4,1).
Ответ: (3,9;4,1) – Б.
Пример 16.9 Решить уравнение (log2x)2-2log2x-3=0 и указать сумму его корней.
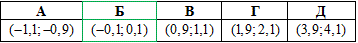
Решение: ОДЗ: x>0.
логарифмическое уравнение
(log2x)2-2log2x-3=0
сведем к квадратному заменой log2x=t.
t2-2•t-3=0
По формулам Виета имеем:
t1+t2=2 – сумма корней уравнения;
t1•t2=3 – их произведение, тогда
t1=-1 и t2=3 – корни квадратного уравнения.
Возвращаемся к замене, и вычисляем простые логарифмические уравнения
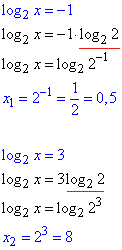
Оба корня принадлежат ОДЗ, по условию найдем их сумму:
x1+x2=0,5+8=8,5.
Ответ: 8,5 – Д.
С простых примеров на раскрытие логарифмических уравнений Вы увидели, что достаточно знать несколько формул и базовые свойства логарифма и уже можно самостоятельно решать уравнения. Для простых условий это работает, но напоминаем, что курс ВНО подготовки содержит 40 примеров, причем ряд задач сочетают в себе не только логарифмы, но и корни, модули, показательные выражения. Вы научитесь сводить уравнения к квадратным, логарифмировать и еще много чего нового.
]]>Геометрический смысл квадратного уравнения
Графиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения - это точки пересечения параболы с осью абсцисс (х). Из этого следует, что есть три возможных случая:
1) парабола не имеет точек пересечения с осью абсцисс. Это означает, что она находится в верхней плоскости с ветками вверх или нижней с ветками вниз. В таких случаях квадратное уравнение не имеет действительных корней (имеет два комплексных корня).
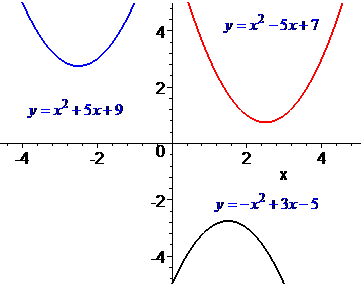
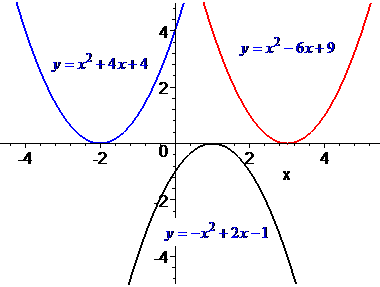
2) парабола имеет одну точку пересечения с осью Ох. Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня).
3) Последний случай на практике интересный больше - существует две точки пересечения параболы с осью абсцисс. Это означает, что существует два действительных корня уравнения.
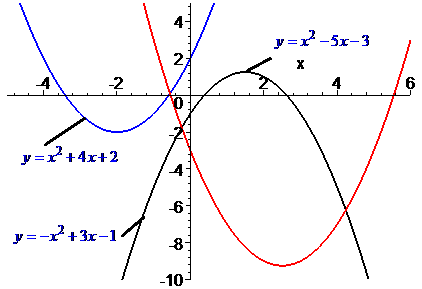
На основе анализа коэффициентов при степенях переменных можно сделать интересные выводы о размещении параболы.
1) Если коэффициент а больше нуля то парабола направлена ветками вверх, если отрицательный - ветки параболы направлены вниз.
2) Если коэффициент b больше нуля то вершина параболы лежит в левой полуплоскости, если принимает отрицательное значение - то в правой.
Вывод формулы для решения квадратного уравнения
Перенесем константу с квадратного уравнения
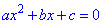
за знак равенства, получим выражение
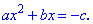
Умножим обе части на 4а
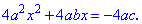
Чтобы получить слева полный квадрат добавим в обеих частях b^2 и осуществим преобразование
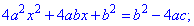
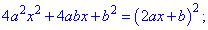
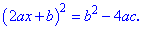
Отсюда находим
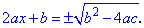
Формула дискриминанта и корней квадратного уравнения
Дискриминантом называют значение подкоренного выражения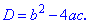 Если он положительный
Если он положительный 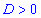 то уравнение имеет два действительных корня, вычисляемые по формуле
то уравнение имеет два действительных корня, вычисляемые по формуле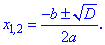 При нулевом дискриминант
При нулевом дискриминант 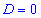 квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0
квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0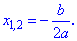 При отрицательном дискриминант
При отрицательном дискриминант 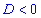 уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле
уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле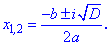
Теорема Виета
Рассмотрим два корня квадратного уравнения 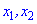 и построим на их основе квадратное уравнение.
и построим на их основе квадратное уравнение.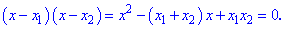 С записи легко следует сама теорема Виета: если имеем квадратное уравнение вида
С записи легко следует сама теорема Виета: если имеем квадратное уравнение вида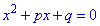 то сумма его корней равна коэффициенту p, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q. Формульная запись вышесказанного будет иметь вид
то сумма его корней равна коэффициенту p, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q. Формульная запись вышесказанного будет иметь вид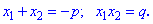 Если в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета.
Если в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета.
Расписание квадратного уравнения на множители
Пусть поставлена задача: разложить квадратное уравнение на множители. Для его выполнения сначала решаем уравнение (находим корни). Далее, найденные корни подставляем в формулу разложения квадратного уравнения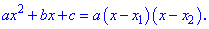 На этом задача будет разрешен.
На этом задача будет разрешен.
Задачи на квадратное уравнение
Задача 1. Найти корни квадратного уравнения
x^2-26x+120=0.
Решение: Запишем коэффициенты 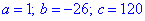 и подставим в формулу дискриминанта
и подставим в формулу дискриминанта
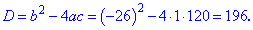
Корень из данного значения равен 14, его легко найти с калькулятором, или запомнить при частом использовании, однако для удобства, в конце статьи я Вам дам список квадратов чисел, которые часто могут встречаться при подобных задачах.
Найденное значение подставляем в формулу корней
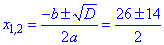
и получаем
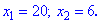
Задача 2. Решить уравнение
2x2+x-3=0.
Решение: Имеем полное квадратное уравнение, выписываем коэффициенты и находим дискриминант
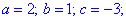
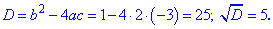
По известным формулам находим корни квадратного уравнения
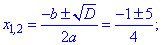
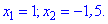
Задача 3. Решить уравнение
9x2-12x+4=0.
Решение: Имеем полное квадратное уравнение. Определяем дискриминант
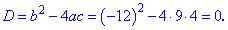
Получили случай когда корни совпадают. Находим значения корней по формуле
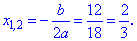
Задача 4. Решить уравнение
x^2+x-6=0.
Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
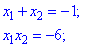
С второго условия получаем, что произведение должно быть равно -6. Это означает, что один из корней отрицателен. Имеем следующую возможную пару решений{-3;2}, {3;-2}. С учетом первого условия вторую пару решений отвергаем.
Корни уравнения равны 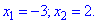
Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см2.
Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х – большую сторону, тогда 18-x меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
х(18-х)=77;
или
х2-18х+77=0.
Найдем дискриминант уравнения
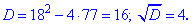
Вычисляем корни уравнения
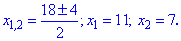
Если х=11, то 18-х=7, наоборот тоже справедливо (если х=7 , то 21-х=9).
Задача 6. Разложить квадратное 10x2-11x+3=0 уравнения на множители.
Решение: Вычислим корни уравнения, для этого находим дискриминант
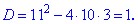
Подставляем найденное значение в формулу корней и вычисляем
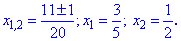
Применяем формулу разложения квадратного уравнения по корнями
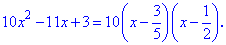
Раскрыв скобки получим тождество.
Квадратное уравнение с параметром
Пример 1. При каких значениях параметра а, уравнение (а-3)х2+(3-а)х-1/4=0 имеет один корень?
Решение: Прямой подстановкой значения а=3 видим, что оно не имеет решения. Далее воспользуемся тем, что при нулевом дискриминанте уравнение имеет один корень кратности 2. Выпишем дискриминант
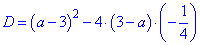
упростим его и приравняем к нулю
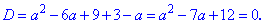
Получили квадратное уравнение относительно параметра а, решение которого легко получить по теореме Виета. Сумма корней равна 7, а их произведение 12. Простым перебором устанавливаем, что числа 3,4 будут корнями уравнения. Поскольку решение а=3 мы уже отвергли в начале вычислений, то единственным правильным будет - а=4. Таким образом, при а=4 уравнение имеет один корень.
Пример 2. При каких значениях параметра а, уравнение а(а+3)х^2+(2а+6)х-3а-9=0 имеет более одного корня?
Решение:Рассмотрим сначала особые точки, ими будут значения а=0 и а=-3. При а=0 уравнение упростится до вида 6х-9=0; х=3/2 и будет один корень. При а= -3 получим тождество 0=0.
Вычислим дискриминант
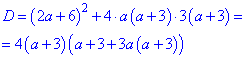
и найдем значения а при котором оно положительно
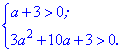
С первого условия получим а>3. Для второго находим дискриминант и корни уравнения
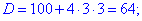
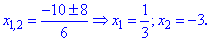
Определим промежутки где функция принимает положительные значения. Подстановкой точки а=0 получим 3>0. Итак, за пределами промежутка (-3;1/3) функция отрицательная. Не стоит забывать о точке а=0, которую следует исключить, поскольку в ней исходное уравнение имеет один корень.
В результате получим два интервала, которые удовлетворяют условию задачи
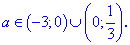
Подобных задач на практике будет много, постарайтесь разобраться с заданиями самостоятельно и не забывайте учитывать условия, которые взаимоисключают друг друга. Хорошо изучите формулы для решения квадратных уравнений, они довольна часто нужны при вычислениях в разных задачах и науках.
Формула дискриминанта
Дискриминант D квадратного уравнения a*x^2+bx+c=0 равен D=b^2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 - уравнение имеет 1 корень (2 совпадающих корня):
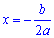 D<0 – не имеет действительных корней (в школьной теории). В ВУЗах изучают комплексные числа и уже на множестве комплексных чисел уравнение с отрицательным дискриминантом имеет два комплексных корня.
D<0 – не имеет действительных корней (в школьной теории). В ВУЗах изучают комплексные числа и уже на множестве комплексных чисел уравнение с отрицательным дискриминантом имеет два комплексных корня.
Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту [email protected].
Общая формула для нахождения корней квадратного уравнения:
Корни уравнения находим по формуле
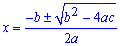
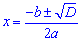 Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
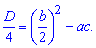 В таких случаях корни уравнения находят по формуле
В таких случаях корни уравнения находят по формуле
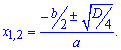
Вторая способ нахождения корней - это Теорема Виета.
Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
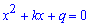 Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
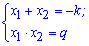 Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
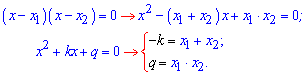 Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни
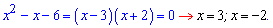
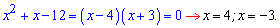
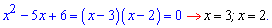
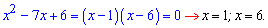
До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла - "Зачем школьникам квадратное уравнение?", "Какой физический смысл дискриминанта?".
Давайте попробуем разобраться, что описывает дискриминант?
В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
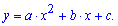 Так вот физический смысл квадратного уравнения - это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Так вот физический смысл квадратного уравнения - это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
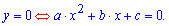 Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0),
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0),
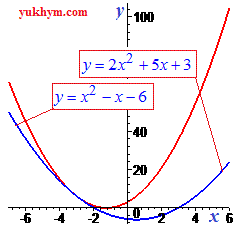 или парабола ветвями вниз (a<0).
или парабола ветвями вниз (a<0).
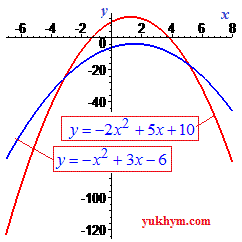 Вершина параболы лежит посередине между корнями
Вершина параболы лежит посередине между корнями
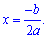
Физический смысл дискриминанта:
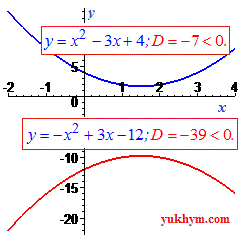
Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox.
 Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
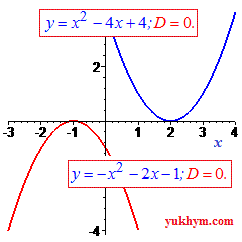 И последний случай, когда дискриминант меньше нуля (D<0) – график параболы принадлежит плоскости над осью абсцисс (ветки параболы вверх), или график полностью под осью абсцисс (ветки параболы опущены вниз).
И последний случай, когда дискриминант меньше нуля (D<0) – график параболы принадлежит плоскости над осью абсцисс (ветки параболы вверх), или график полностью под осью абсцисс (ветки параболы опущены вниз).
Неполные квадратные уравнения
Если в квадратном уравнении коэффициент при свободном члене или переменной равны нулю то такие уравнения называют неполными. Корни уравнений находим по упрощенной формуле
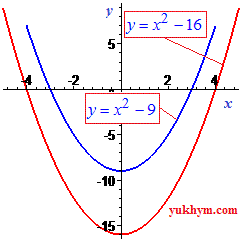
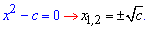 График функций всегда симметричен относительно начала координат. Стоит отметить, что уравнение имеет действительные корни только тогда, когда в уравнении чередуются знаки при коэффициентах "+, -" или "-, +".
График функций всегда симметричен относительно начала координат. Стоит отметить, что уравнение имеет действительные корни только тогда, когда в уравнении чередуются знаки при коэффициентах "+, -" или "-, +".
 Неполное квадратное уравнение вида
Неполное квадратное уравнение вида
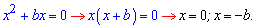 одним из корней всегда имеет точку x=0.
одним из корней всегда имеет точку x=0.
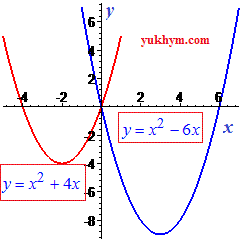 В таком контексте решения квадратных уравнений становится нужным, а при построении графиков парабол, еще и визуально интересным времяпрепровождением, особенно если речь идет о школьном занятии по анализу графика функций, или изучении темы парабол. Поэтому в 8, 9 классе рекомендуем эти две темы в алгебре сочетать.
В таком контексте решения квадратных уравнений становится нужным, а при построении графиков парабол, еще и визуально интересным времяпрепровождением, особенно если речь идет о школьном занятии по анализу графика функций, или изучении темы парабол. Поэтому в 8, 9 классе рекомендуем эти две темы в алгебре сочетать.
Если материал помог Вам в обучении, просьба поделиться с друзьями ссылкой на статью!
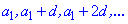
в которой каждый последующий член отличается от предыдущего на сталое слагаемое, которое еще называют шагом или разницей прогрессии.
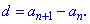
Таким образом, задавая шаг прогрессии и ее первый член можно найти любой ее элемент по формуле
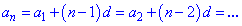
Свойства арифметической прогрессии
1) Каждый член арифметической прогрессии, начиная со второго номера является средним арифметическим от предыдущего и следующего члена прогрессии
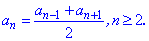
Обратное утверждение также верно. Если среднее арифметическое соседних нечетных (четных) членов прогрессии равно члену, который стоит между ними, то данная последовательность чисел является арифметической прогрессией . По этим утверждением очень просто проверить любую последовательность.
Также по свойству арифметической прогрессии, приведенную выше формулу можно обобщить до следующей
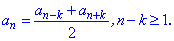
В этом легко убедиться, если расписать слагаемые справа от знака равенства
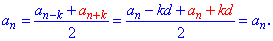
Ее часто применяют на практике для упрощения вычислений в задачах.
2) Сумма n первых членов арифметической прогрессии вычисляется по формуле
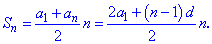
Запомните хорошо формулу суммы арифметической прогрессии, она незаменима при вычислениях и довольно часто встречается в простых жизненных ситуациях.
3) Если нужно найти не всю сумму, а часть последовательности начиная с k-го ее члена, то в Вам пригодится следующая формула суммы
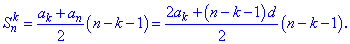
4) Практический интерес представляет отыскание суммы n членов арифметической прогрессии начиная с k-го номера . Для этого используйте формулу
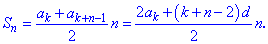
На этом теоретический материал заканчивается и переходим к решению распространенных на практике задач.
Пример 1. Найти сороковой член арифметической прогрессии 4;7;...
Решение:
Согласно условию имеем
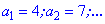
Определим шаг прогрессии
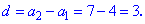
По известной формуле находим сороковой член прогрессии 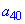
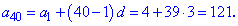
Пример2. Арифметическая прогрессия задана третьим и седьмым ее членом 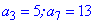 . Найти первый член прогрессии и сумму десяти.
. Найти первый член прогрессии и сумму десяти.
Решение:
Распишем заданные элементы прогрессии по формулам
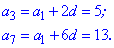
От второго уравнения вычтем первое, в результате найдем шаг прогрессии
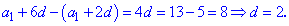
Найденное значение подставляем в любое из уравнений для отыскания первого члена арифметической прогрессии
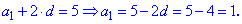
Вычисляем сумму первых десяти членов прогрессии
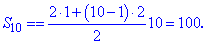
Не применяя сложных вычислений ми нашли все искомые величины.
Пример 3. Арифметическую прогрессию задано знаменателем 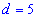 и одним из ее членов
и одним из ее членов 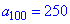 . Найти первый член прогрессии, сумму 50 ее членов начиная с 50 и сумму 100 первых.
. Найти первый член прогрессии, сумму 50 ее членов начиная с 50 и сумму 100 первых.
Решение:
Запишем формулу сотого элемента прогрессии
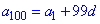
и найдем первый
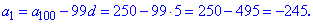
На основе первого находим 50 член прогрессии
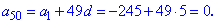
Находим сумму части прогрессии
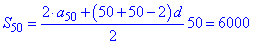
и сумму первых 100
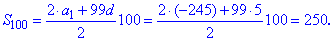
Сумма прогрессии равна 250.
Пример 4.
Найти число членов арифметической прогрессии, если:
а3-а1=8, а2+а4=14, Sn=111.
Решение:
Запишем уравнения через первый член и шаг прогрессии и определим их
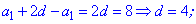
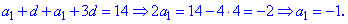
Полученные значения подставляем в формулу суммы для определения количества членов в сумме
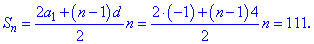
Выполняем упрощения
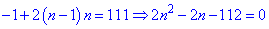
и решаем квадратное уравнение
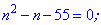
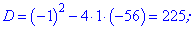
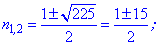
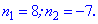
Из найденных двух значений условии задачи подходит только число 8 . Таким образом сумма первых восьми членов прогрессии составляет 111.
Пример 5.
Решить уравнение
1+3+5+...+х=307.
Решение: Данное уравнение является суммой арифметической прогрессии. Выпишем первый ее член и найдем разницу прогрессии
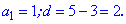
Найденные величины подставим в формулу суммы прогрессии для отыскания числа слагаемых
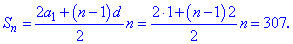
Как и в предыдущем задании, выполним упрощения и решим квадратное уравнение
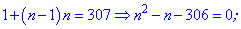
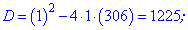

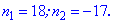
Выбираем более логичное из двух значений . Имеем, что сумма 18 членов прогрессии с заданными величинами а1=1, d=2 равна Sn=307.
На этом знакомство с арифметической прогрессией только начинается. В книгах вы найдете много подобных задач, методика решений которых не была рассмотрена . Приведенного материала должно хватить Вам с головой, чтобы разобраться и решить задачи самостоятельно. Если же нет то обращайтесь и мы Вам поможем с вычислениями.
Похожие материалы:
]]>
Для полного задания геометрической прогрессии кроме знаменателя необходимо знать или определить первый ее член. Для положительного значения знаменателя 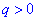 прогрессия является монотонной последовательностью, причем если
прогрессия является монотонной последовательностью, причем если 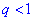 это последовательность чисел является монотонно убывающей и при
это последовательность чисел является монотонно убывающей и при 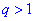 монотонно возрастающей. Случай, когда знаменатель равен единице
монотонно возрастающей. Случай, когда знаменатель равен единице 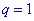 на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
на практике не рассматривается, поскольку имеем последовательность одинаковых чисел, а их суммирование не вызывает практического интереса
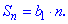
Общий член геометрической прогрессии вычисляют по формуле
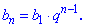
Сумма n первых членов геометрической прогрессии определяют по формуле
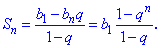
Рассмотрим решения классических задач на геометрическую прогрессию. Начнем для понимания с простейших.
Пример 1. Первый член геометрической прогрессии равен 27, а ее знаменатель равен 1/3. Найти шесть первых членов геометрической прогрессии.
Решение: Запишем условие задачи в виде
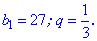
Для вычислений используем формулу n-го члена геометрической прогрессии
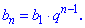
На ее основе находим неизвестные члены прогрессии
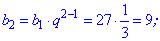
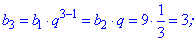
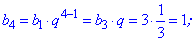
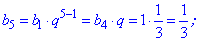
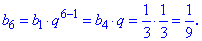
Как можно убедиться, вычисления членов геометрической прогрессии несложные. Сама прогрессия будет выглядеть следующим образом
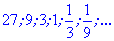
Пример 2. Даны три первых члена геометрической прогрессии 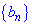 : 6; -12; 24. Найти знаменатель и седьмой ее член.
: 6; -12; 24. Найти знаменатель и седьмой ее член.
Решение: Вычисляем знаменатель геомитрической прогрессии исходя из его определения
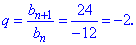
Получили знакопеременную геометрическую прогрессию знаменатель которой равен -2. Седьмой член вычисляем по формуле
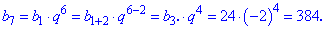
На этом задача решена.
Пример 3. Геометрическая прогрессия 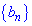 задана двумя ее членами
задана двумя ее членами 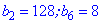 . Найти десятый член прогрессии.
. Найти десятый член прогрессии.
Решение:
Запишем заданные значения через формулы
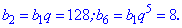
По правилам нужно было бы найти знаменатель, а затем искать нужное значение, но для десятого члена имеем
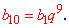
Такую же формулу можно получить на основе нехитрых манипуляций с входными данными. Разделим шестой член ряда на другой, в результате получим
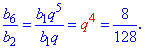
Если полученное значение умножить на шестой член, получим десятый
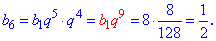
Таким образом, для подобных задач с помощью несложных преобразований в быстрый способ можно отыскать правильное решение.
Пример 4. Геометрическая прогрессия задано рекуррентными формулами
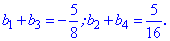
Найти знаменатель геометрической прогрессии и сумму первых шести членов.
Решение:
Запишем заданные данные в виде системы уравнений
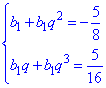
Выразим знаменатель разделив второе уравнение на первое
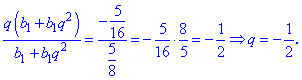
Найдем первый член прогрессии из первого уравнения
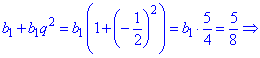
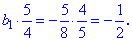
Вычислим следующие пять членов для нахождения суммы геометрической прогрессии
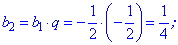
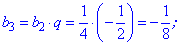
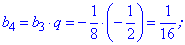
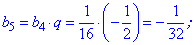
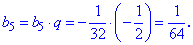
Поскольку найти сумму в данном случае не составляет большого труда, то обходя простые выкладки сводим все слагаемые под общий знаменатель
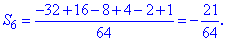
В общем случае, при нахождении суммы знакопеременных рядов следует выделять их положительную часть и отрицательную и найти отдельно их суммы по приведенным выше формулам. Наконец найденные значения добавить.
Примеры на геометрическую прогрессию не так сложны если знать несколько базовых формул. Все остальное сводится к простым математическим манипуляциям. Практикуйте с примерами самостоятельно и подобные задания будут для Вас несложными.
Похожие материалы:
]]>Группа Б (уровень 2)
Пример 1. В арифметической прогрессии а8=12,4; a23=4,7. Вычислить сумму а14+a17.
Решение: Представим 14 член прогрессии через 8 и 17 через 23. В виде формул они будут запись
a14=а8+6d;
a17=a23-6d.
Находим искомую сумму членов прогрессии
a14+a17=a8+6d+a23-6d=a8+a23;
a14+a17=12,4+4,7=17,1.
Ответ: сумма равна 17,1.
Пример 2. В геометрической профессии b4=3; b17=14,7. Вычислить произведение b9*b12.
Решение: Учитывая свойства геометрической прогрессии, запишем ее 9 член через 4, а 12 через 17.
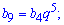
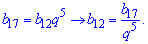
Видим, что при умножении знаменатель геометрической прогрессии упрощается
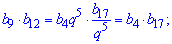
b9*b14=3*14,7=44,1.
Ответ: произведение равно 44,1.
Пример 3. Сумма п первых членов арифметической прогрессии выражается формулой Sn=3n2+6n. Вычислить a6.
Решение: Найдем первый член прогрессии и сумму первых двух
a1=S1=3+6=9;
a1+a2=2a1+d=S2=3*2^2+6*2=24.
Из второго уравнения, учитывая значение первого члена, находим шаг прогрессии
d=24-2a1=24-2*9=6.
По общей формуле вычисляем 6 член арифметической прогрессии
a6=a1+5d=9+5*6=39.
Ответ: a6=39.
Пример 4. Сумма п первых членов арифметической прогрессии выражается формулой Sn=n2+5n. Вычислить a10.
Решение: Задача идентичное предыдущей, только на этот раз попробуем решить по другой методике. Используем сумму арифметической прогрессии в виде
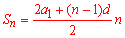
Подставим в эту формулу заданную зависимость суммы и приравняем коэффициенты при одинаковых степенях n
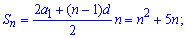
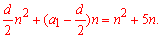
Это и есть важная формула, из которой находим первый член прогрессии и разность (шаг)
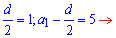
d=2; a1=5+d/2=6.
Вычисляем 10 член прогрессии
a10=a1+9d=6+9*2=24.
Ответ: a10=24.
Пример 5. Вычислить сумму всех четных натуральных чисел до 100 включительно.
Решение: Первый элемент последовательности равен a1=2, последний равен 100. От 1 до 10 имеем 5 четных чисел. В сотни всего 10 десятков то есть 10*5 четных чисел. Если рассуждать по-другому, то половина элементов до 100 четные, половина - нечетные.
100/2=50 – количество четных чисел.
Разница прогрессии равна 2.
Далее подставляем известные значения в формулу и вычисляем
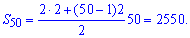
Сумма четных чисел до 100 равна 2550.
Ответ: S50=2550.
Пример 6. Вычислить сумму всех двузначных чисел.
Решение: Номер члена прогрессии будет равен его значению
a1=1;… a99=99.
Разница прогрессии равна единице d=1. Находим сумму арифметической прогрессии по формуле
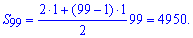
Сумма равна 4950.
Ответ: S99=4950.
Пример 7. В арифметической прогрессии а2+a11=10, а5+a6=13. Вычислить разницу прогрессии.
Решение: Аглоритм решения подобных примеров следующий: Выражаем члены прогрессии через один, имеющий наименьший порядковый номер
a11=a2+9d;
a5=a2+3d;
a6=a2+4d.
Подставляем ету запись в сумму членов прогрессии
a2+a2+9d=2*a2+9d=10;
a2+3d+a2+4d=2*a2+7d=13.
Есть два уравнения с двумя неизвестными. Для отыскания разницы прогрессии от первого уравнения вычитаем второе
9d-7d=2d=10-13;
2d=-3; d=-1,5.
Ответ: d=-1,5.
Пример 8. В арифметической прогрессии а2+a11=10, а5+a6=13. Вычислить a1.
Решение: Задача аналогична предыдущей. Выражаем, для удобства, все члены суммы через 1 номер
a2=a1+d; a11=a1+10d;
a5=a1+4d; a6=a1+5d.
Подставляем в формулы и составляем уравнение
a1+d+a1+10d=2*a1+11d=10;
a1+4d+a1+5d=2*a1+9d=13.
От первого уравнения вычтем второе и найдем шаг прогрессии
11d-9d=2d=10-13=-3.
2d=-3; d=-1,5.
Зная шаг прогрессии, первый ее элемент находим из уравнения
2*a1+9*(-1,5)=13; 2*a1=13+13,5=26,5;
a1=26,5/2=13,25.
Ответ: a1=13,25.
Пример 9. Вычислить сумму всех двузначных натуральных чисел которые при делении на 3 дают в остатка 2.
Решение: Сначала запишем общую формулу члена прогрессии для данной задачи. Учитывая условие получим зависимость
a[n]=3*n+2.
Первое двузначное число, которое удовлетворяет условию это 11.
a[3]=3*3+2=11.
Последнее число равно 98 и оно соответствует 32 номеру прогрессии
a[32]=3*32+2=98.
Дальше есть выбор из двух вариантов - искать частичную сумму прогрессии или от полной суммы вычесть первых два элемента. Поступим по второй схеме
a1=3+2=5; a2=3*2+2=8;
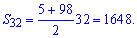
От найденной суммы вычитаем первые два элемента прогрессии
S=1648-5-8=1635.
Ответ: S=1635.
Пример 10. Вычислить сумму всех двузначных натуральных чисел которые при делении на 4 дают в остатка 1.
Решение: Выпишем общую формулу члена прогрессии
a[n]=4*n+1.
Всегда поступайте таким образом для описания прогрессии.
Первое нужное число равно 13. Его легко получить взяв несколько членов прогрессии – 5; 9;13; ...
С последним номером немного больше поисков, но можно установить, что это будет 97.
a[3]=13; a[24]=97.
Шаг прогрессии составляет d=4.
Находим сумму двузначных натуральных чисел
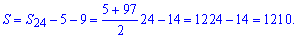
Получили в сумме 1210.
Ответ: S=1210.
Пример 11. Вычислить сумму всех нечетных натуральных чисел от 13до 81 включительно.
Решение: Запишем формулу нечетных чисел.
a[n]=2*n+1, n=0; 1; …
Сделаем замену в прогрессии так, чтобы элемент под первым номером был равен 13.
a[n]=2*n+1=13.
Отсюда n=6. Значит новая прогрессия выходит с предыдущей добавлением к индексу n+1=6; n=5.
b[n]=2(n+5)+1.
Найдем под каким номером в прогрессии идет число 81.
2*(n+5)+1=81;
n+5=(81-1)/2=40; n=35.
Итак b[35]=81.
Находим сумму первых 35 членов прогрессии
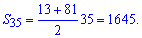
Следовательно, искомая сумма равна 1645.
Второй метод заключается в нахождении суммы прогрессии a[n] с определенного ее номера. Для этого нужно знать формулу, которую порой нет возможности на контрольных или тестах выводить из формулы суммы прогрессии
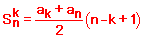
Если Вы ее знаете, то в этом случае нужную найти сумму от 6 до 40 члена прогрессии a[n]
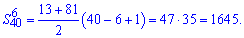
И на "закуску" третий способ, который заключается в вычитании из полной суммы прогрессии суммы ее первых членов.
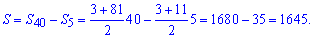
На этом вычисления примера завершены.
Ответ: S=1645.
Пример 12. В арифметической прогрессии а18=12,3; a32=2,8. Вычислить а21+a29.
Решение: Если Вы внимательно просмотрели ответы в предыдущих примерах то знаете как поступить в этом задании. Сначала выражаем 21 и 29 член прогрессии через 18 и 32.
a21=a18+(21-18)d=a18+3d;
a29=a32+(29-32)d=a32-3d.
Легко видеть, что при суммировании разница прогрессии пропадает
a21+a29=a18+a32=12,3+2,8=15,1.
Ответ: сумма равна 15,1.
Пример 13. Сумма п первых членов арифметической прогрессии выражается формулой Sn=13n2+5n. Вычислить разницу прогрессии.
Решение: Подобная задача рассматривали под номером 3, 4. Запишем общую формулу суммы прогрессии и приравняем к заданной
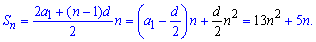
Приравняем коэффициенты при квадрате номера прогрессии
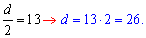
Разница прогрессии равна 26
Ответ: d=26.
Пример 14 Сумма п первых членов арифметической прогрессии выражается формулой Sn=3n2+8n. Вычислить разницу прогрессии.
Решение: Здесь не будем Вас утомлять и по аналогии с предыдущим примером запишем, что коэффициент при квадрате индекса равен половине разницы прогрессии
d/2=3; d=3*2=6.
Видим, наскоько просто найти разницу прогрессии.
Ответ: d=6.
Пример 15. В геометрической прогрессии bm-n=7,2; bm=9,6. Вычислить bm+n
Решение: На вид задания на геометрическую прогрессию сложное. Однак простые формулы позволяют вычислить все.
Запишем bm через предварительный известный член прогрессии bm-n
b[m]=b[m-n]*q^n.
Такое же выполним для bm+n
b[m+n]= b[m]*q^n.
Осталось из первого уравнения выразить знаменатель прогрессии
q^n= b[m]/b[m-n]
и подставить во второе
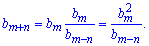
Подставим заданные значения в формулу
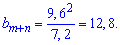
Искомый член геометрической прогрессии равен 12,8.
Ответ: b[m+n]=12,8.
Пример 16. В геометрической прогрессии bm+n=6,3; bm=4,2. Вычислить bm-n
Решение: Этот пример построен по обратному принципом к предыдущему, однако ход вычислений подобный. Из анализа значений геометрической прогрессии следует, что bm-n должен быть меньше bm=4,2. А аналогии с предыдущим примером позволяют припустить, что ответом будет квадрат меньшего числа разделен на большее значение.
bm-n= bm* bm/bm+n
и сейчас Вы в этом убедитесь.
Запишем следующие члены геометрической прогрессии через предыдущие
b[m]=b[m-n]*q^n;
b[m+n]= b[m]*q^n.
С первой зависимости находим bт-п, а з 2 – q^n.
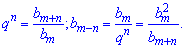
Выполним соответствующие расчеты
b[m-n]=4,2*4,2/6,3=2,8.
Ответ: b[m-n]=2,8.
Пример 17. В арифметической прогрессии ат+п=1,4; ат-п=92,8. Вычислить ат.
Решение: Неизвестный член арифметической прогрессии равен среднему арифметическому соседних элементов. Поскольку ат+п и ат-п есть равноудалены елементами прогрессии от ат , то его находим по формуле
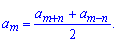
a[m]=(92,8+1,4)/2=47,1.
Ответ a[m]=47,1.
Пример 18. В арифметической прогрессии ат =8,75; ат+п=13,8. Вычислить a[m-n]
Решение: Выразим следующие члены прогрессии через предыдущие
a[m+n]=a[m]+n*d;
a[m]=a[m-n]+ n*d.
С первой формулы находим произведение n*d и подставляем во вторую
n*d= a[m+n]-a[m];
a[m-n]=a[m]-n*d=2*a[m]-a[m+n].
Подставим значение в формулу и найдем нужный элемент прогрессии
a[m-n]= 2*8,75-13,8=3,7.
Ответ: a[m-n]=3,7.
Пример 19. В геометрической прогрессии b21*b7=62,7. Вычислить b19 если b9=5,5.
Решение: Задача одна из сложных среди всех которые рассмотренные здесь, однако на практике решить возможно. Запишем все старшие члены геометрической прогрессии через b7
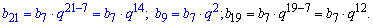
Запишем произведение 21 и 7 члена геометрической прогрессии и расписано b9
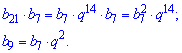
Чтобы получить выражение для 19 члена прогрессии нужно произведение b21*b7 разделить на b9
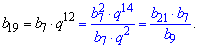
С опытом Вы увидите, что в подобных примерах остается делить одни значения на вторые или умножать, примеры где нужно тянуть корни или подносить к степени в геометрических прогрессиях встречаются крайне редко.
Вычисляем b19
b[19]=62,7/5,5=11,4.
Ответ: b[19]=11,4.
Пример 20. Вычислить сумму первых двадцати членов арифметической прогрессии (аn) если а6 +а9+а12+ а15 = 20 .
Решение: Выглядит на первый взгляд непонятно, как с такой записи получить сумму. Однако, если вспомнить формулу суммы арифметической прогрессии, то все что там фигурирует - это первый и последний член суммы, а также их количество. Таким образом следует представить сумму заданных членов прогрессии через первый и последний элемент. Уверяю Вас, что разница прогрессии в расчетах упростится и заданное условие не что иное, как удвоенная сумма первого и 20 члена прогрессии. В этом Вы сейчас наглядно убедитесь. Расписываем первые два слагаемые суммы через a [1], а остальные через a[20].
a[6]=a[1]+5d;
a[9]=a[1]+8d;
a[12]=a[20]-8[d];
a[15]=a[20]-5d.
Просуммировав их всех получим
a[6]+a[9]+a[12]+a[15]=2*a1+2*a[20].
Формула суммы 20 членов арифметической прогрессии имеет вид
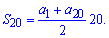
Числитель дроби и является заданной суммой, разделенной на 2 Поэтому сразу выполняем вычисления
S[20]=20/2/2*20=100.
Ответ: S[20]=100.
Пример 21. Сумма первого и пятого членов арифметической прогрессии равна 28,а произведение четвертого и третьего членов 280. Вычислить сумму первых десяти членов прогрессии.
Решение: В этом задании и подобных нужно составлять систему уравнений. Для этого запишем сначала условие задания в виде
a[1]+a[5]=28; a[3]*a[4]=28.
Поскольку 3 член прогрессии является равноудален от 1 и 5, то их среднее арифметическое и будет 3 членом прогрессии
a[3]=(a[1]+a[5])/2=28/2=14.
Произведение распишем через 3 член прогрессии
a[3]*a[4]=a[3]*(a[3]+d)=280;
14*(14+d)=280.
Отсюда находим разницу прогрессии
14+d=280/14=20;
d=20-14=6.
Вычислим 1 и 10 член арифметической прогрессии
a[1]=a[3]-2d=14-2*6=2;
a[10]=a[3]+7d=14+7*2=28.
Есть все необходимые елементы для вычисления суммы прогрессии
S[10]=(2+28)*10/2=150.
Ответ: S[10]=150.
Пример 22. Знайты четыре числа которые образуют геометрическую прогрессию в которой третий член больше первого на 9, а второй больше четвертого на 18. В ответе записать их сумму.
Решение: Запишем условие задачи в виде
b[3]-b[1]=9; b[2]-b[4]=18.
Распишем члены геометрической прогрессии через 1 элемент
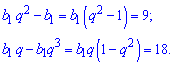
Поделив второе уравнения на первое получим знаменатель прогрессии
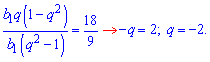
Из первого уравнения находим 1 член геометрической прогрессии
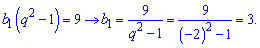
Все остальные члены прогрессии получаем умножением предыдущего номера на знаменатель.
b[2]=b[1]*q=3*(-2)=-6;
b[3]=b[2]*q=-6*(-2)=12;
b[4]=12*(-2)=-24.
Осталось вычислить сумму членов геометрической прогрессии
S=3-6+12-24=-15.
Ответ: S=-15.
Пример 23. Знаменатель геометрической прогрессии 1/3, третий член геометрической прогрессии 1/9, а сумма всех членов геометрической прогрессии 13/9. Найти количество членов геометрической прогрессии.
Решение: Сумма членов геометрической прогрессии находим по формуле
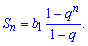
Найдем первый член прогрессии через 3 и знаменатель.
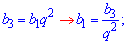
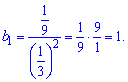
Подставим значение в формулу суммы и найдем количество суммируемых членов
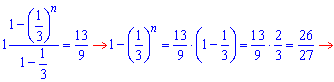
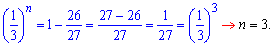
Итак, получили 3 члена геометрической прогрессии.
Ответ: n=3.
Пример 24. Дано две арифметические прогрессии. Первый и пятый члены первой прогрессии соответственно равны 7 и -5. Первый член второй прогрессии равна 0, а последний 7/2. Вычислить сумму членов второй прогрессии если известно,что третьи члены обеих прогрессий равны между собой.
Решение: Запишем условие примера
a[1]=7;a[5]=-5;
b[1]=0; b[n]=7/2;
a[3]=b[3]; S[n]-?
Найдем 3 член первой прогрессии через среднее арифметическое соседних
a[3]=(a[1]+a[5])/2=(7-5)/2=1.
Учитывая что
b[3]=a[3]=1,
найдем шаг второй прогрессии.
b[3]=b[1]+2*d;
1=0+2*d; d=1/2=0,5.
Найдем номер последнего члена второй прогрессии
b[n]=0+(n-1)d=7/2=3,5;
n-1=3,5/d=3,5/0,5=7;
n=7+1=8.
Вычислим сумму восьми членов прогрессии
S[8]=(0+3,5)*8/2=3,5*4=14.
Ответ: S[8]=14.
После такой практиктики я думаю Вы знаете как находить сумму арифметической и геометрической прогрессии. Если нет ознакомьтесь с примерами изначально (это была шутка).
Похожие материалы:
Если примеры были полезны Вам - посоветуйте их друзьям.
]]>Группа А (уровень 1)
Пример 1. Вычислить шестой член арифметической прогрессии 21,3; 22,4; …,
Решение: Найдем разницу (шаг) прогрессии
d=a2-a1=22,4-21,3=1,1.
Далее вычисляем шестой член арифметической прогрессии
a6=a1+(6-1)d=21,3+5*1,1=26,8.
Пример 2. Вычислить шестой член геометрической прогрессии 5; 10; 20; ...
Решение: Найдем знаменатель геометрической прогрессии
q=b2/b1=10/5=2.
Вычисляем шестой член геометрической прогрессии
b6=b1q6-1=5*25=5*32=160.
Пример 3. В арифметической прогрессии a1=2,1 a10=12,9. Вычислить разницу прогрессии.
Решение: Представим десятый член прогрессии в виде формулы
a10=a1+(10-1)d= a1+9d.
Подставим известные значения и решим
12,9=2,1+9d;
9d=12,9-2,1=10,8;
d=10,8/9=1,2.
Ответ: разница прогрессии d=1,2.
Пример 4. В геометрической прогрессии b1=2,56; b4=4,42368. Вычислить знаменатель прогрессии.
Решение: Находим знаменатель прогрессии
q=b2/b1=4,42368/2,56=1,728.
Без калькулятора здесь не обойтись.
Ответ: знаменатель прогрессии равен q=1,728.
Пример 5. В арифметической прогрессии a1=20,1, d=1,3. Вычислить сумму первых восьми членов прогрессии.
Решение: Cуму арифметической прогрессии находим по формуле
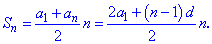
Выполняем вычисления
S8=(2*20,1+(8-1)*1,3)*8/2=197,2.
Ответ: S8=197,2.
Пример 6. В геометрической прогрессии b1=1,5; q=1,2. Вычислить сумму первых четырех членов прогрессии.
Решение: Cуму геометрической прогрессии вычисляем по формуле
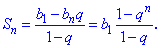
Находим сумму прогрессии
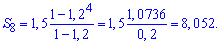
Ответ: S8=8,052.
Пример 7. В арифметической прогрессии a1=1,35 d=-2,4. Вычислить номер члена прогрессии, равный -25,05.
Решение: Член арифметической прогрессии находят по формуле
an=a1+(n-1)d.
По условию задано все кроме порядкового номера известно, найдем его
-25,05=1,35+(n-1)(-2,4);
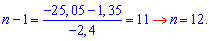
Ответ: n=12.
Пример 8. Вычислить седьмой член прогрессии 23,5; 24,82; 26,14; ...
Решение: Поскольку в условии не задано какая прогрессия задана, то сначала нужно ето установить . Получите, что арифметическая
d=a2-a1=24,82-23,5=1,32;
d=a3-a2=26,14-24,82=1,32.
Находим седьмой член прогрессии
a7=a1+(7-1)d=23,5+6*1,32=31,42.
Ответ: a7= 31,42.
Пример 9. Вычислить номер члена прогрессии 2,1; 3,3; 4,5; ... , равный 11,7.
Решение: Легко убедиться, что задана арифметическая прогрессия. Найдем разницу прогрессии
d=a2-a1=3,3-2,1=1,2.
По формуле члена прогрессии
an=a1+(n-1)d
найдем номер
11,7=2,1+(n-1)*1,2;
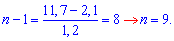
Ответ: n= 9.
Пример 10. Вычислить четвертый член прогрессии 1,5; 1,8; 2,16; ....
Решение: Без проверки можно сказать, что прогрессия - геометрическая. Найдем ее знаменатель
q=b2/b1=1, 8/1,5=1,2.
Вычислим 4 член геометрической прогрессии по формуле
b4=b1q3=1,5*1,23=2,592.
Ответ: b4=2,592.
Пример 11. Вычислить номер члена прогрессии 1,2; 1,8; 2,16; ... равный 4,05.
Решение: Имеем геометрическую прогрессию. Найдем знаменатель прогрессии
q=b2/b1=1, 8/1,2=1,5.
Найдем номер прогресии из зависимости
bn=b1qn-1.
4,05=1,2*1,5n-1;
1,5n-1=4,05/1,2=3,375=1,53;
n-1=3; n=4.
Ответ: n=4.
Пример 12. В арифметической прогрессии a5=14,91 a9=20,11. Вычислить a1.
Решение: Выразим 9 член прогрессии через 5
a9= a5+(9-5)d
и найдем шаг прогрессии
20,11=14,91+4d;
4d=5,2; d=5,2/4=1,3.
Выразим 5 член прогрессии через 1 и вычислим первый
a5= a1+4d;
14,91= a1+5,2;
a1=14,91-5,2=9,71.
Ответ: a1=9,71.
Пример 13. В арифметической прогрессии а7=12,01; a11=17,61. Вычислить разницу прогрессии.
Решение: Выразим 11 член прогрессии через 7
a11= a7+(11-7)d.
Отсюда вычислим шаг прогрессии
17,61=12,01+4d;
4d=5,6; d=5,6/4=1,4.
Ответ: d=1,4.
Пример 14. В геометрической прогрессии b5=64; b8=1. Вычислить b3.
Решение: Выразим 8 член прогрессии через 5
b8= b5q8-5.
Отсюда находим знаменатель прогрессии
1=64 q3;
q3=1/64=(1/4)3;
q=1/4.
Подобным образом находим b3 через b5
b3= b5/q2=64*42=1024.
Ответ: b3=1024.
Пример 15. В арифметической прогрессии а9+а15=14,8. Вычислить а12
Решение: В этом примере следует учесть, что 12 член прогрессии находится посередине между 9 ее номером и 15. Поэтому соседние члены прогрессии (9, 15) можно выразить через 12 следующим образом
a9= a12-(12-9)d;
a15= a12+(15-9)d;
a9= a12-3d;
a15= a12+3d.
Просуммируем крайние члены прогрессии
a9+ a15= a12-3d+ a12+3d=2a12.
Отсюда находим 12 член прогрессии
a12=(a9+a15)/2=14,8/2=7,4.
Ответ: a12=7,4.
Пример 16. В геометрической прогрессии b10*b14=289. Вычислить модуль 12 члена прогрессии | b12|.
Решение: Алгоритм решении задачи содержится в предыдущем примере. Следует выразить 10 и 14 член геометрической прогрессии через 12. По свойствам геометрической прогрессии получим
b10= b12/q2; b14= b12*q2.
Легко заметить, что при их произведения знамениик прогрессии пропадает
b10* b14= (b12)2=289=172.
Отсюда находим модуль | b12|
(b12)2=289=172 -> | b12|=17.
Ответ: | b12|=17.
Пример 17. В геометрической прогрессии b8=1,3. Вычислить b6*b10.
Решение: Схема вычислений аналогична предыдущему примеру - выражаем 6 и 10 член прогрессии через 8.
b6= b8/q2; b10= b8*q2.
При их умножении знаменатели сокращаются и получим квадрат известного члена прогрессии
b6*b10= (b8)2=1,32=1,69.
Ответ: b6*b10=1,69.
Пример 18. В арифметической прогрессии а10=3,6: a12=8. Вычислить а8
Решение: Запишем члены прогрессии в ряд а8, а10, a12. Между ними одинаковый шаг, найдем его
a12= a10+2d;
2d= a12- a10=8-3,6=4,4.
Таким же методом находим а8
a10= a8+2d;
a8= a10-2d=3,6-4,4=-0,8.
Вот такие несложные расчеты.
Ответ: a8=-0,8.
Пример 19. В геометрической прогрессии b14=8; b16=2. Вычислить b12.
Решение: Опуская подробные объяснения, запишем произведение 14 и 16 члена прогрессии
b14*b16=(b12)2.
Это равносильно среднему геометрическому. Найдя корень из произведения членов, получим искомое значение
(b12)2=8*2=16; b12=4.
Ответ: b12=4.
Пример 20. В арифметической прогрессии а5=3,4; a11=6,9. Вычислить а17.
Решение: Между 5,11 и 17 членом прогрессии одинаковый шаг и он равен 6d. Поэтому конечное решение можно записать в виде
а17= a11+6d= a11+(a11- а5)=2*6,9-3,4=10,4.
Думаю, что Вы понимаете, почему такая запись. Если нет - попробуйте расписать 11 член прогрессии через 5 и виразить 6d.
Ответ: а17=10,4.
Пример 21. Вычислить 6-й член геометрической прогрессии 3; 12;... .
Решение: Найдем знаменатель прогрессии
q=b2/b1=12/3=4.
Воспользуемся общей формуле члена геометрической прогрессии
bn= b1*qn-1.
Отсюда получим
b6= b1*q5=b2*q4.
Как видите, главное в записи, чтобы сумма индекса (2) и степень (4) соответствовала порядковому номеру члена прогрессии (6). Выполняем вычисления
b6= 12*44=12*256=3072.
Получили большое число, но геометрическая прогрессия тем и отличается, что ее члены или быстро растут, или - сходят.
Ответ: b6=3072.
Пример 22. В арифметической прогрессии а3=48; a5=42. Вычислить а7.
Решение: Так как разница прогрессии между заданными членами и искомым сталая и равна 2d то формула 7 члена прогрессии будет выглядеть
а7= a5+2d= a5+(a5- а3);
а7=2*42-48=36.
Ответ: а7=36.
Пример 23. Вычислить сумму первых пятнадцати нечетных чисел.
Решение: Запишем несколько членов этой прогрессии 1, 3, 5, ... Разница прогрессии равна d=2. Вычислим 15 член прогрессии
а15= а1+14d=1+14*2=29.
Подставим в формулу суммы арифметической прогрессии
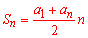
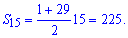
Ответ: Сумма прогрессии равна 225.
Пример 24. Вычислить первый член арифметической прогрессии, если сумма первых двенадцати ее членов равна 642 и двенадцатый член равен 48.
Решение: Здесь нужно составить два уравнения из которых определить две неизвестные. Сумму 12 членов арифметической прогрессии можно найти по формуле
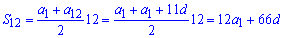
12а1+66d=642.
Второе уравнение запишем с формулы 12 члена прогрессии
а12= а1+11d=48.
Выразим 11d из второго уравнения и подставим в первое уравнение
11d=48-а1;
12а1+6*11d=642;
12а1+6*(48-а1)=642;
6а1+288=642;
6а1=642-288=354;
а1=354/6=59.
Ответ: а1=59.
Пример 25. Вычислить знаменатель геометрической прогрессии, состоящей из действительных чисел, если b5=162; b8=4374.
Решение: Выразим 8 член геометрической прогрессии через 5
b8= b5*q3.
Отсюда выразим знаменатель
q3= b8/ b5=4374/162=27=33; q=3.
Знаменатель равен 3.
Ответ: q=3.
На этом простые задачи на арифметическую и геометрическую прогрессию назад. Хорошо разберите приведены варианты и схемы вычислений, они не слишком сложные и понятно обоснованы.
Похожие материалы:
]]>Пример 1. В геометрической прогрессии b10* b14* b21=-0,125. Вычислить b15.
Решение. Приведем методику которая упростит решение подобных примеров. Для начала найдем сумму индексов членов прогрессии.
10+14+21=45.
Сумма 45 нацело делится на 15 и получаем 3. Заданное произведение членов прогресии можно представить в виде
b10* b14* b21=(b15)^3
Это следует и со свойств геометрической прогреси.
Отсюда вычисляем искомый член прогрессии
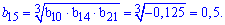
Итак, 15 член прогрессии равен -0,5.
Пример 2. Сумма трех чисел, представляющих возрастающую арифметическую прогрессию равна 21. Если к ним, соответственно, добавить 2, 3, и 9 то образованные числа составят геометрическую прогрессию. Найти наибольшее из искомых членов проргресии.
Решение. Таким заданием можно проверить знание формул арифметической и геометрической прогрессии.
Обозначим члены возрастающей прогрессии через a-d, a, a+d.
Тогда их сумма равна 3a=21, откуда a=21/3=7.
Такое быстрое решение получили за счет удачного выбора формул членов прогресии. Таким образом средний член арифметической прогрессии известен.
Далее найдем неизвестные члены геометрической прогрессии
Первый – a-d+2=7-d+2=9-d
второй a+3=7+3=10.
третий a+d+9=7+d+9=16+d.
По свойству геометрической прогрессии о среднем геометрическом значении получим что квадрат среднего ее члена равен произведению равноудаленных, т.е.
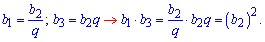
Подставим члены геометрической прогрессии в формулу
(9-d)(16+d)=10^2=100.
Думаю Ви знаете что делать с подобным уравнением.
Раскроем скобки и сведем к квадратному уравнению относительно разницы арифметической прогрессии.
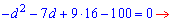
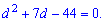
Находим дискриминант
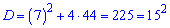
и шаг арифметической прогрессии
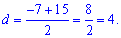
Отсюда находим нужный член арифметической прогрессии
a+d=7+4=11.
Вот такие сложные задачи на прогрессию Вам могут встретиться в обучении.
Пример 3. Три числа которые составляют возрастающую арифметическую прогрессию дают в сумме 15. Если к первому и второму из них добавить по единице, а к третьему числу прибавить 4, то новые числа составят геометрическую прогрессию. Найти старшый член заданной прогресии.
Решение. Задача аналогична предыдущей. Вводим те же обозначения что и в предыдущем примере, тогда средний член арифметической прогрессии равен 15/3=5, а соседние – 5-d и 5+d.
По условию запишем члены геометрической прогрессии
(5-d+1)=6-d; 5+1=6; 5+d+4=9+d
и составим из них уравнение
(6-d)(9+d)=6*6=36.
Раскрываем скобки и сводим к квадратному уравнению
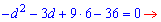
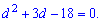
Вычисляем дискриминант
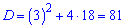
и разницу арифметической прогрессии
d=(-3+9)/2=3.
Больший из членов прогресии равен 8
a+d=5+3=8.
Пример 4. Три числа b1, b2, b3 образуют возрастающую геометрическую прогрессию. Вычислить b3 если b1*b2*b3=64, b1+b2+b3=14.
Решение. Опять имеем задание на составление уравнения. Обозначим члены геометрической прогрессии в нужном для нас виде
b/q;b;b*q.
Подставив в условие можно найти средний член геометрической прогрессии
b/q*b*b*q=b^3=64.
Отсюда средний член геометрической прогрессии равен корню кубическому из 64
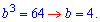
С учетом найденного значения, запишем второе условие задания
b1+b2+b3=14;
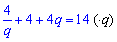
Умножым на знаменатель прогресии
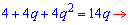
и сведем к квадратному уравнению

Вычислим дискриминант уравнения
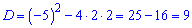
и знаменатель геометрической прогрессии
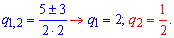
Второе значение отбрасываем, так как при нем геометрическая прогрессия становится убывающей, а по условию мы ищем возрастающую прогрессию.
Теперь без труда находим старший член геометрической прогрессии
b*q=4*2=8.
Пример 5. Три числа b1, b2, b3 образуют убивающую геометрическую прогрессию. Вычислить b3 если b1*b2*b3=27, b1+b2+b3= 13.
Решение. По свойству геометрической прогрессии имеем
b2/q*b2*b2*q=2^3=27.
Отсюда второй член геометрической прогресии равен b[2]=3.
Из второго условия получим уравнение
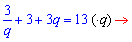
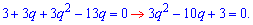
Найдем дискриминант квадратного уравнения
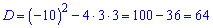
и определим знаменатель прогрессии
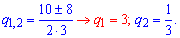
Первое значение q=3 не удовлетворяет начальное условие (убивающая прогресия).
При q=1/3 третий член геометрической прогрессии равен
b[3]=b[2]*q=3/3=1.
Рекомендуем используйте приведенный алгоритм вычислений в подобных задачах.
Пример 6. Определить седьмой член возрастающей арифметической прогрессии если а3+а9=24, а3*а9=108.
Решение. Задача не сложная, поскольку имеем два условия и две неизвестные. Так что решение найти можно. Выразим из первого уравнения a[9] и подставим во второе
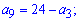
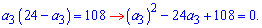
Последнее уравнение решаем через дискриминант
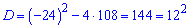
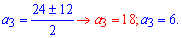
С первого условия
а3+а9=24
видим, что при а3=18 прогрессия не будет возрастающей. Итак, остается а3=6. Отсюда
a[9]=24-a[3]=24-6=18.
С другой стороны
a[9]=a[3]+6d
имеем условие для нахождения разницы прогрессии
6+6d=18; 6d=12; d=12/6=2.
По формуле находим седьмой член арифметической прогрессии
a[7]=a[3]+4d=6+4*2=14.
Вот и весь алгоритм подобных вычислений.
Пример 7. Определить восьмой член возрастающей арифметической прогрессии если а2+а7=18, а2*а7=56.
Решение. Подобнаяе по схеме вычислений задача уже рассматривалась. Выразим из первого уравнения a[2] и подставим во второе
a[2]=18-a[7]; (18-a[7]) a[7]=56.
Раскроеем скобки и сведем к квадратному уравнению
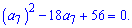
С помощью дискриминанта
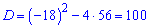
вычислим неизвестный член прогрессии
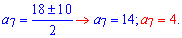
С первого условия делаем вывод что только при a[7]=14 арифметическая прогрессия будет возрастающей.
Соответственно второй член прогресии равен
a[2]=18-a[7]=18-14=4.
По формуле
a[7]=a[2]+5d
определяем шаг прогрессии
14=4+5d; 10=5d; d=2.
Находим 8 член арифметической прогрессии
a[8]=a[7]+d=14+2=16.
Для самопроверки можете подставить найдены члены прогрессии в условие задания.
Пример 8. Вычислить сумму первых восьми членов нисходящей арифметической прогрессии если а2+а6=24, а2*а6=128.
Решение. Чтобы найти сумму прогрессии нам нужно знать первый и восьмой член прогрессии, или 1 член прогрессии и разность (шаг).
Для начала определим из двух уравнений хотя бы один член прогрессии
a[2]=24-a[6];
(24-a[6])*a[6]=128.
При раскрытии скобок получим квадратное уравнение
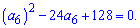
Как решать квадратные уравнения Вы уже знаете. Дискриминант принимает значение
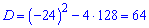
Далее считаем 6 член арифметической прогрессии
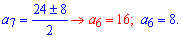
При a[6]=8 арифметическая прогрессия является убывающей. Находим разницу прогрессии
a[2]=24-a[6]=24-8=16.
a[6]=a[2]+4d=16+4d=8;
4d=-8;d=-2.
Легко заметить что значение второго члена прогрессии всегда совпадает с корнем уравнения который отвергаем по условию задачи. Это своего рода подсказка правильности вычислений.
Находим первый и восьмой член прогрессии
a[1]=a[2]-d=16-(-2)=18;
a[8]=a[6]+2d=8+2*(-2)=4.
Найденные значения подставляем в формулу суммы арифметической прогрессии
S=(a[1]+a[8])*8/2=(18+4)*8/2=88.
Сумма восьми членов прогрессии равна 88.
Конечно это не все примеры, которые можно встретить в интернете среди возможных, однако и на их базе можно взять для себя несколько удачных приемов которые можно использовать на практике при решении упражнений на арифметическую и геометрическую прогрессии. Навыки приходят с практикой, поэтому ищите подобные задачи и учитесь решать!
Похожие материалы:
]]> . Вычислить логарифм значит найти такой степень x (
. Вычислить логарифм значит найти такой степень x (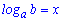 ),при котором выполняется равенство
),при котором выполняется равенство 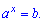
Основные свойства логарифма
Приведенные свойства необходимо знать, поскольку, на их основе решаются практически все задачи и примеры связаны с логарифмами. Остальные экзотических свойств можно вывести путем математических манипуляций с данными формулами
1. 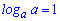
2. 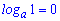
3. 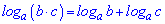
4. 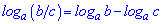
5. 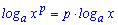
6. 
7. 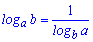
8. 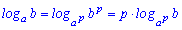
9. 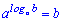
10. 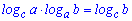
11. 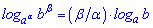
12. 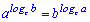
13. 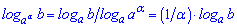
14. 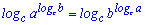
15. 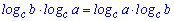
При вычислениях формулы суммы и разности логарифмов (3,4 ) встречаются довольно часто. Остальные несколько сложные, но в ряде задач являются незаменимыми для упрощения сложных выражений и вычисления их значений.
Распространены случаи логарифмов
Одними из распространенных логарифмов такие в которых основание ровное десять, экспоненте или двойке.
Логарифм по основанию десять принято называть десятичным логарифмом и упрощенно обозначать lg(x).
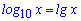
Из записи видно, что основы в записи не пишут. Для примера
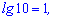
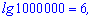
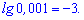
Натуральный логарифм – это логарифм у которого за основу экспонента ( обозначают ln(x)).
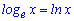
Экспонента равна 2,718281828…. Чтобы запомнить экспоненту можете изучить правило: экспонента равна 2,7 и два раза год рождения Льва Николаевича Толстого. Зная это правило будете знать и точное значение экспоненты, и дату рождения Льва Толстого.
И еще один важный логарифм по основанию два обозначают
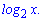
Производная от логарифм функции равна единице разделенной на переменную
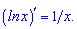
Интеграл или первообразная логарифма определяется зависимостью
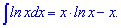
Приведенного материала Вам достаточно, чтобы решать широкий класс задач связанных с логарифмами и логарифмирования. Для усвоения материала приведу лишь несколько распространенных примеров из школьной программы и ВУЗов.
Примеры на логарифмы
Прологарифмировать выражения
Пример 1.
а). х=10ас^2 (а>0,с>0).
По свойствам 3,5 вычисляем
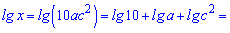
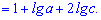
2.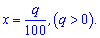
По свойству разницы логарифмов имеем
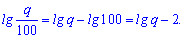
3. 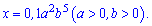
Используя свойства 3,5 находим
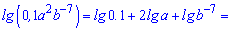
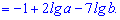
4. 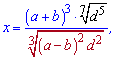 где
где 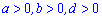 .
.
На вид сложное выражение с использованием ряда правил упрощается к виду
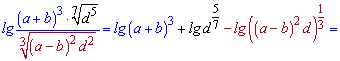
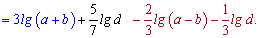
------------------------------------------
Нахождение значений логарифмов
Пример 2. Найти х, если
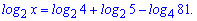
Решение. Для вычисления применим до последнего слагаемого 5 и 13 свойства
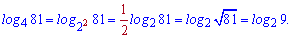
Подставляем в запись и скорбим
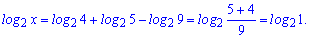
Поскольку основания равные, то приравниваем выражения
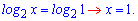
------------------------------------------
Пример 3. Пусть задано значение логарифмов
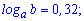
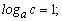
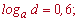
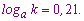
Вычислить log[a](x), если 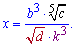
Решение: Прологарифмируем переменную, чтобы расписать логарифм через сумму слагаемых
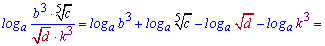
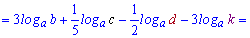
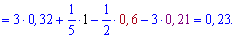
------------------------------------------
На этом знакомство с логарифмами и их свойствами только начинается. Упражняйтесь в вычислениях, обогащайте практические навыки - полученные знания Вам скоро понадобятся для решения логарифмических уравнений. Изучив основные методы решения таких уравнений мы расширим Ваши знания для другой не менее важной теме - логарифмические неравенства ...
]]>