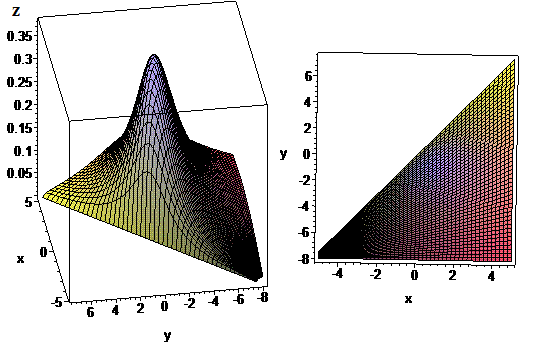Приклад 1. Знайти область визначення вказаних функцій:
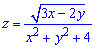
Розв'язання: Маємо дробову функцію, крім цього в чисельнику корінь квадратний. Областю визначення (ОДЗ) будуть всі точки декартової площини в яких знаменник не перетворюється в нуль+підкореневий вираз приймає невід'ємні значення. Разом ці дві умови складають систему з двох рівнянь
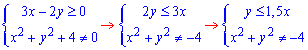
Знаменник завжди більший нуля і лише чисельник обмежує область визначення 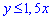 .
.
Таким чином область визначення заданої функції є півплощина, яка знаходиться нижче прямої 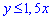 , включаючи саму пряму також.
, включаючи саму пряму також.
Фрагмент просторового графіку ф-ї 2 змінних та її області визначення наведено нижче
Для побудови використано математичний пакет Maple, про його переваги над іншими пакетами на сайті чимало інформації.
Все, що потрібно - це ввести наступний код
> restart;with(plots):
> z:=sqrt(3*x-2*y)/(x^2+y^2+4);
> plot3d(z,x=-5..5,y=-8..1.5*x);
Покрутивши графіком, можна отримати наступні форми
Приклад 2. Знайти частинні похідні і частинні диференціали по кожній змінній від функції:
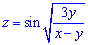 Розв'язання:Завдання не з легких, оскільки задано складено функцію. Маємо синус від кореневої функції від дробу. Тож беручи похідну за змінною x,y будьте уважні
Розв'язання:Завдання не з легких, оскільки задано складено функцію. Маємо синус від кореневої функції від дробу. Тож беручи похідну за змінною x,y будьте уважні
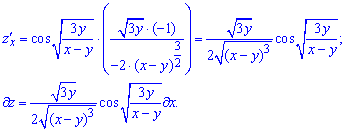
Після знаходження частинних похідних диференціал скласти не проблема.
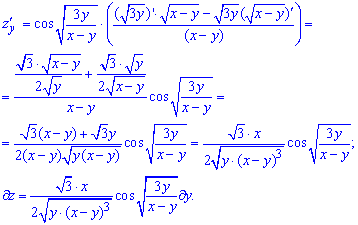
Уважно гляньте, як знайти похідну складеної функції.
Приклад 3. Обчислити значення частинних похідних f'x(M0), f'y(M0), f'z(M0) для заданих функцій f(x;y;z) в точці M0(x0; y0, z0) з точністю до двох знаків після коми: f(x;y;z)=xz/(x-y), M0(3;1;1).
Розв'язання:Завдання не важке, обчислюємо частинні похідні за змінними x,y, далі в формули підставляємо початкову точку. В результаті цього отримаємо
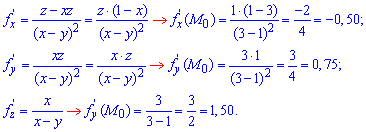
Приклад 4. Знайти повний диференціал функції: z=x2y-4x3y3+2Pi.
Розв'язання:Спершу знаходимо частинні похідні функції z(x,y) за змінною x,y
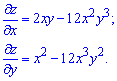
Далі підставляємо їх в формулу повного диференціалу функції
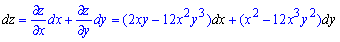
Приклад 5. Обчислити значення похідної складеної функції u=u(x,y), де x=x(t), y=y(t), при t=t0 з точністю до двох знаків після коми: u=ln(e2x+e-2y), x=t2, y=t4, t0=1.
Розв'язання:Подібні завдання Ви скоріш за все вирішували, тому теорії тут розписувати не будемо. Спершу обчислюємо частинні похідні по x, y,t відповідно:
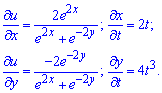
Далі підставляємо їх в формулу похідної складеної функції:
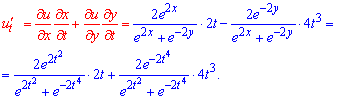
Функція за умовою досить поста, тож маємо мінімум перетворень.
Останнім кроком підставляємо значення параметра в похідну і округлюємо відповідь до двох значень після коми.
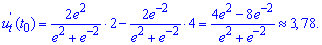
Похідна складеної функції в точці t0=1 приблизно рівна 3,78.
Приклад 6. Обчислити значення частинних похідних функції z(x,y) заданої неявно, в даній точці M0(x0; y0, z0) з точністю до двох знаків після коми: x3-z3+3xyz=27, M0(3; 1, 13).
Розв'язання: Нехай маємо функцію, що задана неявно:
F(x;y;z)=x3-z3+3xyz-27, тоді її частинні похідні в точці M0 приймають значення
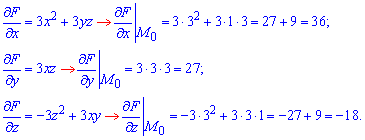
Ось і всі обчислення до даного завдання. Ніколи не лякайтеся умов, а лише вдумливо читайте, що від Вас вимагають.
Приклад 7. Записати рівняння дотичної площини і нормалі до поверхні S в точці : M0(x0; y0, z0):
z=2x2-3y2+4x-2y+10, M0(-1;1, 3).
Розв'язання: Нехай маємо рівняння поверхні:
F(x;y;z)=2x2-3y2+4x-2y-z+10
Обчислимо часткові похідні функції в заданій точці
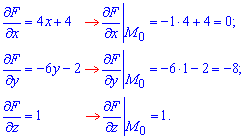
Далі складаємо рівняння дотичної площини:
0(x+1)-8(y-1)+1(z-3)=0 або 8y-z-5=0.
Запишемо рівняння нормалі до поверхні:
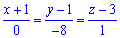
Приклад 8. Знайти другі частинні похідні функції. Переконатися в тому, що мішані похідні рівні між собою z''xy=z''yx:
z=arcsin(4x+2y).
Розв'язання:Знайдемо частинні похідні за обома змінними
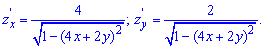
Обчислимо другі частинні похідні заданої функції
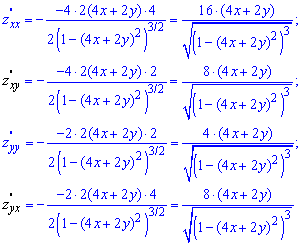
З форму бачимо, що умова рівності мішаних похідних виконується
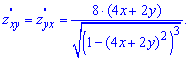
Приклад 9. Перевірити, чи задовольняє вказаному диференціальному рівнянню функція u=u(x,y):
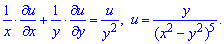
Розв'язання: Знайдемо часткові похідні функції за змінними x,y:
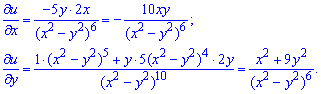
Підставимо знайдені часткові похідні функції у початкове рівняння та спростимо:
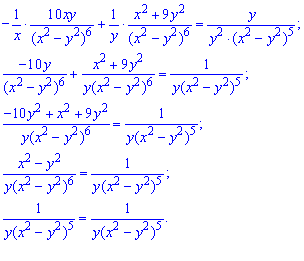
Отримали тотожність, тому задана функція задовольняє вказаному рівнянню.
Приклад 10. Дослідити на екстремум такі функції: z=(x-5)2+y2+1.
Розв'язання: Розділимо дослідження функції двох змінних на екстремум у 3 необхідних етапи:
1) Знайдемо критичні точки - для цього обчислимо часткові похідні
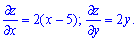
2) З умови рівності часткових похідних нулю складаємо систему рівнянь
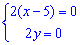
з якої визначаємо точки підозрілі на екстремум звідси x=5; y=0.
3) знайдемо похідну другого порядку в критичній точці A(5;0) :
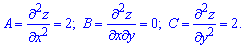
Далі встановимо характер особливості
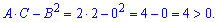
Значення більше нуля, отже в точці (5;0) функція двох змінних має мінімум, а саме zmin=1.
Фрагмент коду в Maple та графік функції в околі точки екстремуму наведено нижче
> restart;with(plots):
> z:=(x-5)^2+y^2+1;
> plot3d(z, x=6..4,y=-1..1);
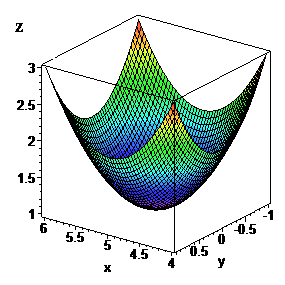
Залишайтеся з нами, на сайті Вас чекає багато готових контрольних робіт з вищої математики та просто якісно підготовлених відповідей до завдань.
Завдання 1. Скласти рівняння геометричного місця точок площини, якщо відношення їх відстані від точки F(6;-3) до відстані до прямої x=2 дорівнює 14/12.
Розв'язання. Нехай маємо шукану точку F1(x;y) і точку на прямій F2(x;y). Відстань між двома точками обчислюється за формулою
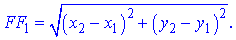
Відстань від точки до прямої є перпендикуляром, тому координати y в даному випадку співпадають
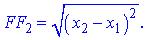
Обчислимо шукані відстані:
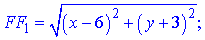
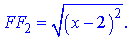
Запишемо відношення даних величин
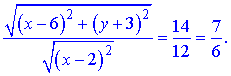
Отримали пропорцію, яка зв'язує потрібні змінні, залишилося її привести до красивого вигляду.
Піднесемо обидві частини до квадрату
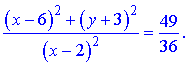
Виконавши ряд перетворень виразимо функцію y через аргумент x
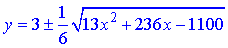 .
.
В декартовій системі координат дана функція матиме наступний вигляд
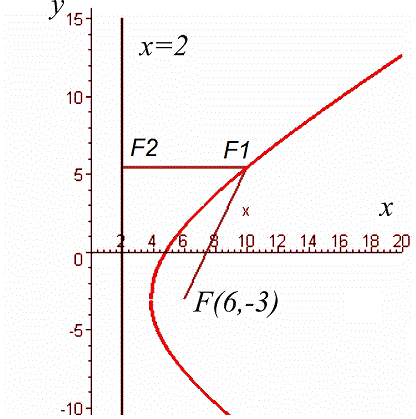
Рівняння після ряду перетворень можна звести до канонічного вигляду
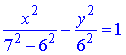
або остаточно
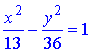
це канонічне рівняння гіперболи.
Розв'язком є права вітка гіперболи з ексцентриситетом е=7/6, директрисою x=2 і фокусом у точці F(6;-3).
Завдання 2. На площині задано 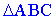 з вершинами A(2;3), B(4;-1), C(-5;1).
з вершинами A(2;3), B(4;-1), C(-5;1).
Потрібно знайти:
1) довжину сторони BC;
2) скласти загальне рівняння медіани, висоти та бісектриси кута A;
3) знайти відстань вершини B від медіани;
4) знайти кут між медіаною і висотою (у градусах).
Розв'язання.
1) Довжину сторони знаходимо за формулою
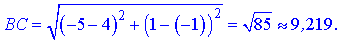
2) Побудуємо рівняння медіани, яка ділить протилежну сторону пополам в точці M(x;y). Знайдемо її координати за формулою середнього арифметичного координат сторони
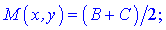
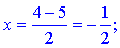
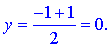
Побудуємо загальне рівняння прямої, що проходить черех точки A(2;3) та M(-0,5;0)
y=A*x+B.
При підстановці точок отримаємо систему із двох рівнянь
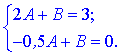
Для відшукання першої невідомої віднімемо від першого рівняння друге
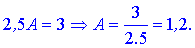
Отримане значення підставляємо в перше рівняння
B=3-2*A=3-2*1,2=0,6.
Рівняння медіани – y=1,2*x+0,6.
Остаточне рівняння медіани, після домноження на 5 і перенесення в ліву сторону, матиме вигляд
6x-5y+3=0.
Складемо загальне рівняння висоти AD. Для цього знайдемо кутовий коефіцієнт сторони BC:
B(4;-1), C(-5;1)
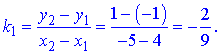
Кутовий коефіцієнт висоти, проведеної з вершини A(2;3) рівний
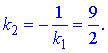
Рівняння висоти, що проходить через точку A має вигляд
y-y1=k1(x-x1);
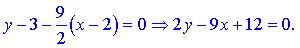
Знайдемо рівняння бісектриси AK. За означенням бісектриса ділить кут пополам, тому 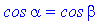 , де
, де
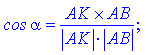
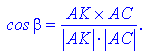
З рівності кутів випливає залежність для визначення рівняння бісектриси
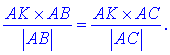
Знайдемо складові рівняння
AB=(4-2; -1-3)=(2;-4),
AC=(-5-2; 1-3)=(-7;-2),
AK=(x-2; y-3),
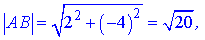
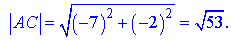
Підставимо знайдені значення у формулу
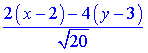
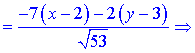
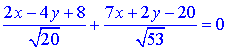
або після спрощень
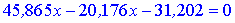
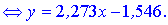
Сам трикутник матиме вигляд
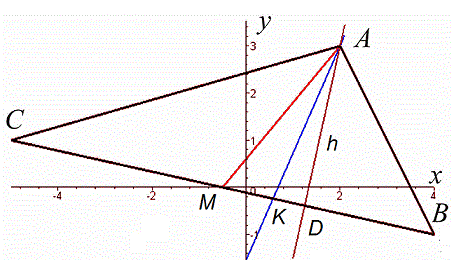
3) Знайдемо відстань від вершини B(4;-1) до медіани 6x-5y+3=0 за форомулою
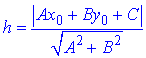
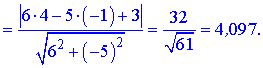
Якщо округлити до десятих, то h=4,1.
4) Маємо дві точки медіани M(-0,5;0), A(2;3) і рівняння висоти 2y-9x+12=0. Виберемо другу точку N з рівняння висоти: при значенні x=0 знаходимо y=-6.
Обчислимо довжини сторін AM(-2,5;-3), AN(-2;-9).
Знайдемо косинус кута між векторами за формулою
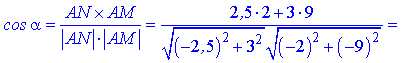
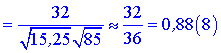
та значення кута в градусах
Всі умови завдання виконано.
Завдання 3. Трикутна піраміда задана вершинами
A1(2;3;1), A2(4;2;1), A3(2;1;0), A4(5;2;10).
Потрібно знайти:
1) рівняння грані A1A2A3;
2) рівняння висоти піраміди, яка проходить через вершину A4;
3) довжину цієї висоти;
4) кут між ребром A1A4 і гранню A1A2A3 в градусах;
5) площу грані A1A2A3;
6) oб'єм піраміди.
Розв'язання.
1) Запишемо рівняння площини у вигляді z=A*x+B*y+C.
Оскільки всі три точки належать цій площині то, підставляючи їх по черзі отримаємо систему рівнянь
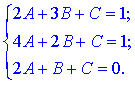
з якої знаходимо невідомі коефіцієнти
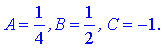
Підставляючи в початкове рівняння, матимемо шукане рівняння грані A1A2A3
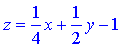 або x+2y-4z-4=0.
або x+2y-4z-4=0.
2) Запишемо рівняння висоти піраміди, яка проходить через вершину A4(5;2;10) на грань
A1A2A3 (x+2y-4z-4=0)
на основі напрямних
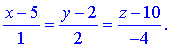
3) Знайдемо висоту, для цього знайдемо довжину сторони
A1A4=(5-2;2-3;10-1)=(3;-1;9).
Враховуючи рівняння грані x+2y-4z-4=0, висоту знайдемо за формулою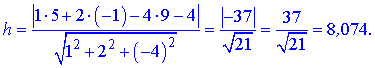
Округлимо до десятих h=8,1.
4) Знайдемо кут між ребром A1A4і гранню A1A2A3 (x+2y-4z-4=0) в градусах.
Запишемо рівняння прямої, що проходить через точки A1(2;3;1), A4(5;2;10)
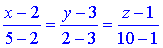
або
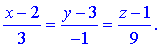
Знайдемо синус кута за формулою
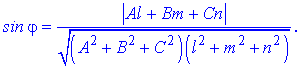
Підставимо значення
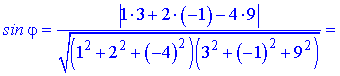
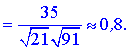
Знаходимо значення кута, яке трохи більше за 53 градуси.
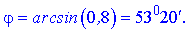
5) Площу грані A1A2A3:
A1(2;3;1), A2(4;2;1), A3(2;1;0)
обчислюємо за формулою половини модулю векторного добутку векторів
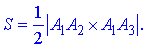
Знайдемо потрібні вектори
A1A2=(4-2;2-3;1-1)=(2;-1;0),
A1A3=(2-2;1-3;0-1)=(0;-2;-1)
та підставимо у формулу площі у скалярній формі
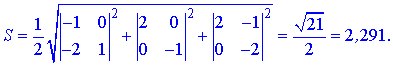
Площа грані рівна 2,3.
6) Обчислимо oб'єм піраміди за формулою
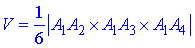
де вектори, що входять рівні
A1A2(2;-1;0), A1A3(0;-2;-1), A1A4(3;-1;9).
Порахувавши визначник
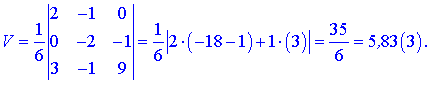
отримаємо, що об'єм піраміди рівний 5,83.
Завдання 4. Дано систему трьох лінійних алгебраїчних рівнянь з трьома невідомими.
Розв'язати систему:
1) за формулами Крамера;
2) засобами матричного числення;
3) методом Гаусса.
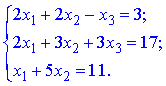
Розв'язання.
1) Застосуємо метод Крамера, для цього обчислюємо визначники 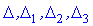
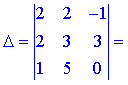
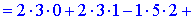
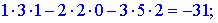
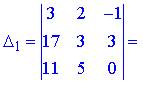
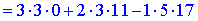
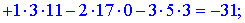
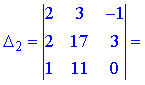
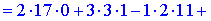
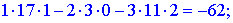
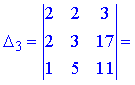
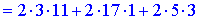
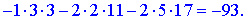
За формулами Крамера знаходимо розв'язки системи рівнянь 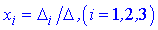
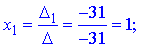
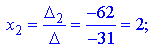
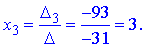
2) Розв'яжемо систему матричним методом. Випишемо матриці та вектори у вигляді
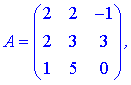
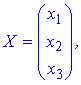
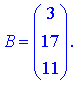
Обчислимо обернену матрицю
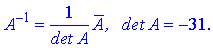
Через визначники другого порядку знаходимо компоненти матриці доповнення
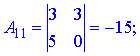
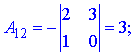
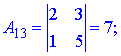
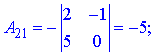
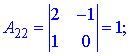
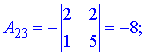
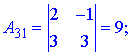
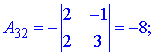
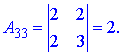
Остаточно, обернена матриця прийме вигляд
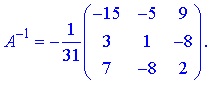
За формулою X=A-1*B знаходимо розв'язок системи рівнянь:
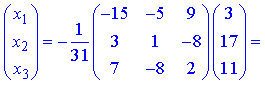
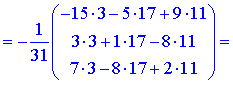
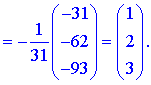
3) Розв'яжемо систему рівнянь методом Гаусса , для цього виписуємо розширену матрицю
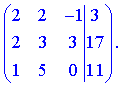
З матрицею виконуємо наступні перетворення: від 2 рівняння віднімемо 2, а від подвоєного 3 віднімемо 1. В результаті отримаємо
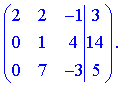
Далі, від другого помноженого на 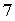 віднімемо третє
віднімемо третє
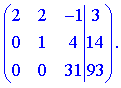
В результаті отримаємо еквівалентну початковій систему рівнянь
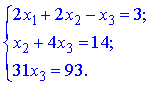
Розв'язуємо дану систему з кінця 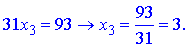
3 другого рівняння маємо 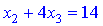
або 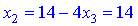
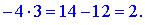
З першого рівняння знаходимо
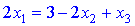
або
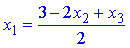
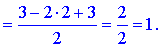
Розв'язок системи рівнянь за Гауссом рівний
x1=1, x2=2, x3=3.
Завдання 5. Звести до канонічного вигляду рівняння кривої другого порядку, використовуючи теорію квадратичних форм. Побудувати стару та нову системи координат і зобразити криву (якщо вона існує).
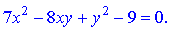
Розв'язання. Виписуємо характеристичне рівняння, яке відповідає заданій кривій
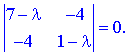
Розв'язавши це рівняння, отримаємо
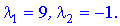
Знайдемо власні вектори, що відповідають власним значенням. Якщо 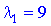 то маємо таку систему рівнянь для знаходження власного вектора
то маємо таку систему рівнянь для знаходження власного вектора 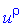
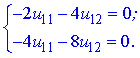
Звідси знаходимо перший вектор 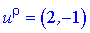 .
.
При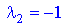 маємо наступну систему рівнянь з якої знаходимо
маємо наступну систему рівнянь з якої знаходимо 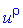
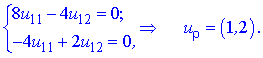
Зводимо власні вектори до одиничних (нормуємо):
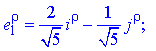
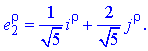
Отже, перетворення координат матиме наступний запис
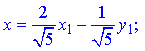
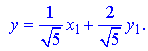
Задане рівняння, після підстановки, стає таким:
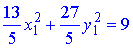
або після спрощення
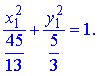
Знайдене канонічне рівняння описує еліпс.
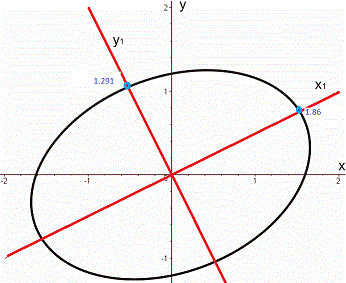
Завдання 6. Обчислити границі (не використовуючи правило Лопіталя):
а) 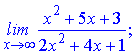
Розв'язання.При змінній прямуючій до безмежності  чисельник і знаменник дробу нескінченно великі. Для знаходження границі виразу чисельник і знаменник ділимо на найвищу степінь кожного
чисельник і знаменник дробу нескінченно великі. Для знаходження границі виразу чисельник і знаменник ділимо на найвищу степінь кожного
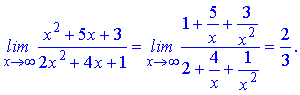
Границя рівна 1/2.
б) 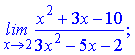
Розв'язання.Обчислимо границі чисельника і знаменника окремо
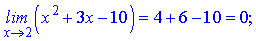
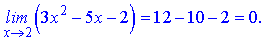
Границі чисельника і знаменника прямують до нуля при при змінній  , а отже отримуємо невизначеність типу нуль поділити на нуль {0/0}.
, а отже отримуємо невизначеність типу нуль поділити на нуль {0/0}.
Теорему про границю частки напряму застосовувати не можна, потрібно знаменник і чисельник скоротити на спільний множник, який прямує до нуля
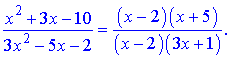
Тоді границя прийме значення
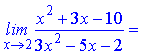
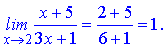
в) 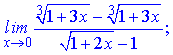
Розв'язання.Границю дробової ірраціональної функції знайдемо, записавши степеневий розклад коренів в чисельнику та знаменнику при змінній прямуючій до нуля 
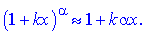
Застосовуючи даний розклад в ряд, знаходимо границю
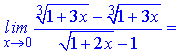
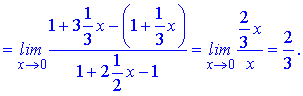
г) 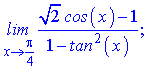
Розв'язання.Легко переконатися, що при підстановці у границі межі 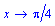
чисельник і знаменник прямують до нуля. Для знаходження границі розкладемо функції cos(x), tan2(x) по степенях змінної в оолі точки x=Pi/4
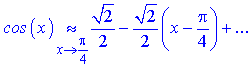
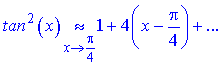
Підставимо отримані значення в границю та спростимо
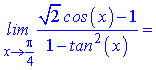
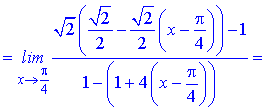
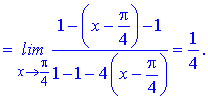
д) 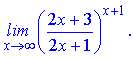
Розв'язання. Зведемо дріб в дужках до формули другої чудової границі
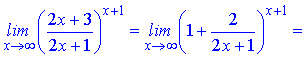
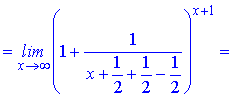
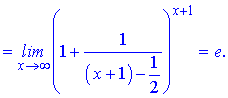
в результаті обчислень отримаємо експоненту.
Завдання 1. Знайти похідні dy/dx заданих функцій.
а) 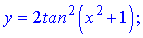
Розв'язання.Виконуємо диференціювання функцій, використовуючи відомі формули для сладеної функції (степеневої)
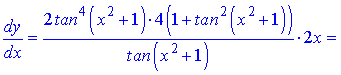
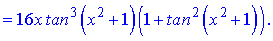
б) 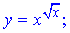
Розв'язання. Тут можна застосувати логарифмічне диференціювання, а можна обійтися формулами похідної для складеної функції
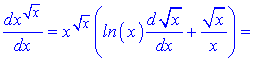
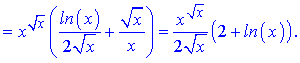
в) 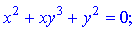
Розв'язання. Знайдемо значення похідної від неявно заданої функції за правилом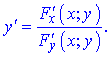
Часткові похідні приймуть значення
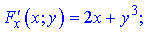
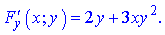
Після підстановки отримаємо таке значення похідної
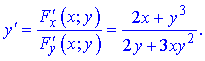
г) 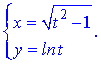
Розв'язання. Знайдемо похідну параметрично заданої функції за правилом
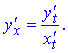
Обчислимо похідні, які входять в залежність
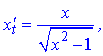
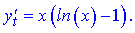
Після спрощення отримаємо такий результат
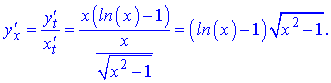
Завдання 2. Доcлідити функцію методами диференціального числення та побудувати її графік
y=x-ln(x+1)
Розв'язання.проходимо всі етапи схеми дослідження функції
1. Область визначення: 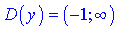
2. Координати точок перетину графіка з осями координат знаходимо з умови y=0, x=0
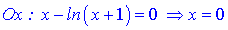
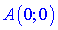
3. Перевірка на парність

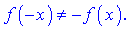
Задана функція ні парна ні непарна, неперіодична.
4. Дослідимо на асимптоти:
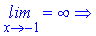
y=-1– вертикальна асимптота.
Рівняння похилої асимптоти має вигляд
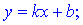
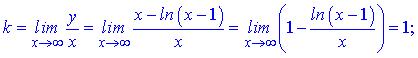
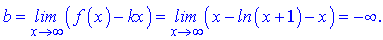
Функціє немає похилої асимптоти.
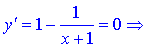
x=0 – точка мінімуму.
5. Графік заданої функції має вигляд:
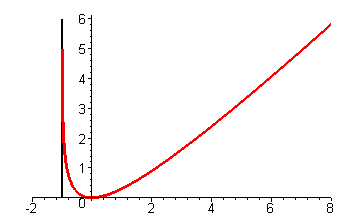
Завдання 3. Із кутів квадратного листа картону розміром 12х12 дм треба вирізати однакові квадрати так, щоб зігнувши лист, одержати коробку найбільшого об'єму. Якою повинна бути сторона вирізаного квадрату ?
Розв'язання. Позначимо через h- сторону відрізаного квадрата. Тоді об'єм знаходимо за формулою
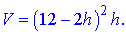
Знайдемо мінімуми і максимуми функції об'єму
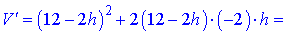
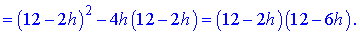
З умови рівності нулю похідної 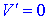 визначаємо точки ектремуму h=2; h=6.
визначаємо точки ектремуму h=2; h=6.
Підставивши дані значення в функцію об'єму V отримаємо, що при h=2 дм об'єм максимальний і рівний
V=128 дм3.
Отже сторона вирізаного квадрата рівна 2 дм.
Завдання 4. Для функції z=f(x;y) знайти частинні похідні другого порядку
z=arctan(xy2)+y2x.
Розв'язання. Здійснюємо диференціювання функціїї за змінною x та y, після чого знаходимо шукані похідні
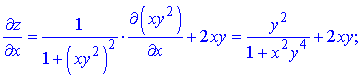
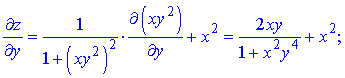
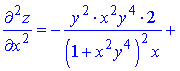
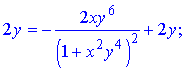
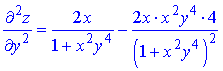
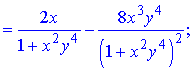
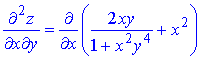
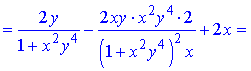
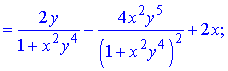
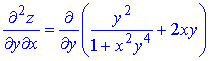
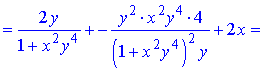
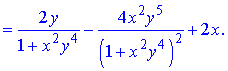
Всі частинні похідні знайдено.
Завдання 5. Дана функція z=f(x;y) і дві точки A(x0;y0) i B(x1;y1).
Обчислити:
1) значення z1 функції в точці B підстановкою координат точки в рівняння поверхні;
2) наближене значення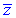 функції в точці B замінивши приріст функції при переході від точки A до точки B диференціалом;
функції в точці B замінивши приріст функції при переході від точки A до точки B диференціалом;
оцінити в процентах відносну похибку при заміні приросту функції її диференціалом;
3) скласти рівняння дотичної площини і нормалі до поверхні z=f(x;y) в точці C(x0;y0;z0)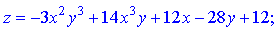
x0=-8;y0=-2
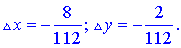
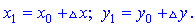
Розв'язання.
1) Знайдемо координати точки B
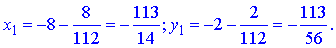
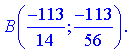
Обчислимо значення функції в цій точці
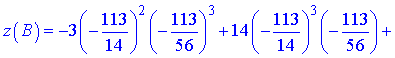
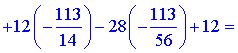
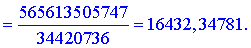
2) Запишемо повний диференціал функції
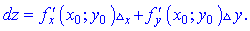
Знайдемо частинні похідні 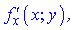
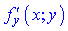
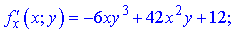
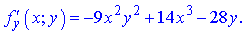
Підставимо початкові точки x0=-8;y0=-2 в знайдені формули
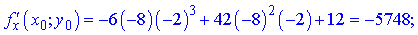
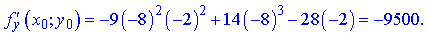
Остаточно диференціал рівний 580,21
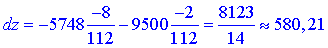
Знайдемо приріст функції dz1 за формулою
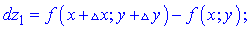
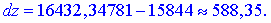
Знайдемо відносну похибку при заміні приросту функції її диференціалом за формулою
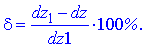
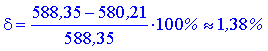
3) Знайдемо значення в точці z(A)
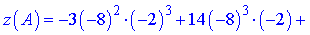
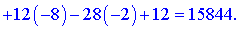
Точка C матиме координати C(-8;-2;15844).
Складемо рівняння дотичної площини за формулою

Продиференціюємо, щоб знайти частинні похідні
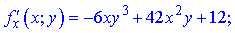
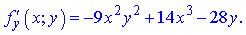
Підставимо знайдене значення C(-8;-2;15844) в отримані залежності
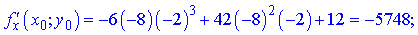
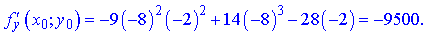
Остаточне рівняння дотичної площини набуде вигляду
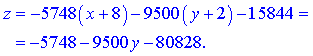
За рівнянням дотичної складаємо рівняння нормалі
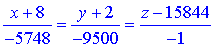
або
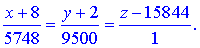
Завдання 6. Знайти найбільше і найменше значення функції z=f(x;y) у замкненій області – трикутнику ABC.
z=x2-4x+y2-32y+12;
A(0;0), B(18;0), C(0;21).
Розв'язання. Знайдемо критичні точки функції, для цього обчислимо частинні похідні та прирівняємо їх до нуля
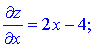
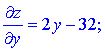
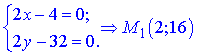
Критична точка M1(2;16) не належить досліджуваній області. А це значить, що функція двох змінних досягає екстремельних значень на сторонах рикутника.
Дослідимо поведінку функції на границях області.
На прямій AB матимемо 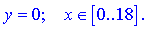
Функція набуде вигляду
z(x,0)=x2-4x+12.
Дослідимо на екстремуми
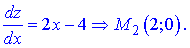
Знайдемо значення функції в цій точці та на краях відрізку
z(A)=12; Z(M2)=8; Z(b)=264.
На прямій AC маємо 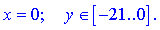
Функція набуде вигляду
z(0,y)=y2-32y+12.
Дослідимо на екстремуми
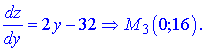
Дана точка не належить проміжку досліджень. Знайдемо значення функції на краях відрізку
z(A)=12; z(C)=1125.
На прямій BC маємо
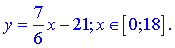
Після підстановки функція z прийме вигляд
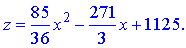
Дослідимо її на екстремуми
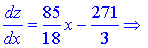
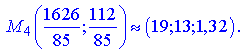
Дана точка не належить досліджуваному проміжку. Значення функції на краях проміжку отримані вище. В розглядуваному трикутнику функція приймає мінімальне і максимальне значення в наступних точках

Подібні контрольні роботи з дослідження функцій, пошуку екстремумів, диференціювання Ви можете зустріти в інтернеті на інших ресурсах. Не лінуйтеся розібратися у їх розв'язанні, це допоможе бути впевненішими при вирішенні контрольних, зрізів, складання іспитів. Також завжди можна знайти свіжі методи вирішення завдань, про які Вам не розповідали на лекціях.
]]> Завдання 1. Розв'язати систему трьох лінійних алгебраїчних рівнянь з трьома невідомими за формулами Крамера
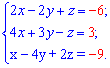
Виконати перевірку розв'язків.
Розв'язання: Знаходимо головний визначник за формулою трикутника
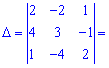
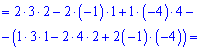
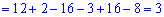
Обчисюємо допоміжні визначники заміною відповідних стовпців на стовпець із вільних членів

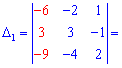
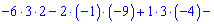
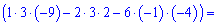
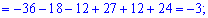
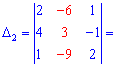
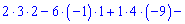
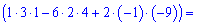
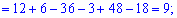
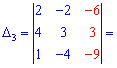
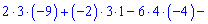
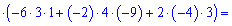
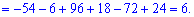
За формулами Крамера обчислюємо розв'язки системи рівнянь
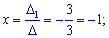
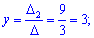
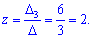
Виконуємо перевірку підстановкою значень
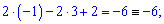
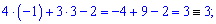
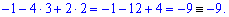
Значення тотожні, отже обчислення виконані правильно.
Завдання 2. Дано координати вершин трикутника А,В,С:
А(3;0), В(5;10), С(13;6).
1) Знайти рівняння сторони АВ.
2) рівняння медіани АМ.
3) рівняння кола, для якого медіана АМє діаметром
Розв'язання:
1) Запишемо умову завдання
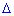 АВС: (3;0), В(5;10), С(13;6).
АВС: (3;0), В(5;10), С(13;6).
АВ=(5-3;10-0)=(2;10)
Модуль вектора АВ рівний
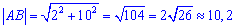
Загальне рівняння прямої, що проходить через точки А і В таке
y=kx+b.
Підставляємо задані точки та зводимо до системи рівнянь
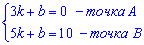
Від другого рівняння віднімаємо перше
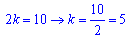
Підставляємо k=5 в друге рівняння
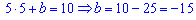
Остаточне рівняння прямої, що проходить через точки А і В таке:
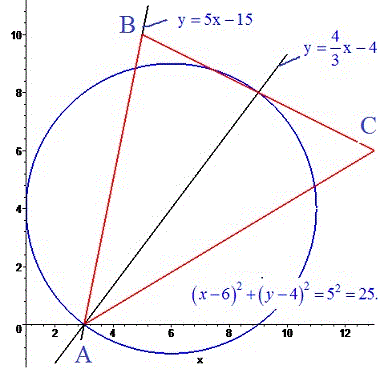
y=5x-15.
2) Знайдемо середину сторони BC, адже медіана АМ буде проходити через цю точку.
М=(B+C)/2;
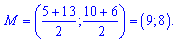
Складаємо рівняння прямої, що проходить через точки
А(3;0); M(9;8);
y=kx+b
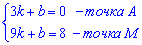
Від другого рівняння віднімаємо перше, помножене на 3
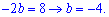
Знайдену невідому підставляємо в перше рівняння
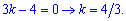
Остаточне рівняння прямої АМ буде наступним
y=4/3*x-4.
3) Знайдемо радіус кола, для якого медіана АМ (А(3;0), M(9;8)) є діаметром
АM=(9-3;8-0)=(6;8);
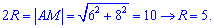
Знайдемо центр кола – точку О.
O=(A+M)/2;
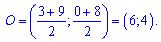
Рівняння кола з центром в точці О(6;4) та радіусом 5 буде наступним.
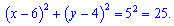
Трикутник та коло наведені нижче
Завдання 3. Знайти границі функцій, не користуючись правилом Лопіталя:
а) 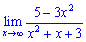
Розв'язання: При змінній прямуючій до безмежності домінуючий вклад вносять доданки, в яких змінна міститься в більшому степені. Виносимо їх за дужки та скорочуємо
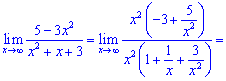
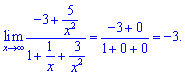
б) 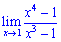
Розв'язання: Чисельник і знаменник перетворюються в нуль у точці x=1. В подібних випадках потрібно скоротити обидві частини на множник, що має особливість. В данному випадку можна було скористатися формулами
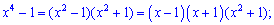
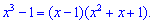
Але такими формулами можна скористатися лише в окремих випадках. В загальному, якщо функція має вигляд поліном розділити на поліном, і вточці знаходження границі x0 обидві перетворюються в нуль то необхідно їх розділити на (x-x0). В даному випадку отримаємо такі розклади для чисельника
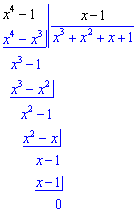
та знаменника відповідно.
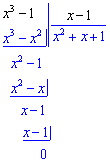
Отримані значення підставляємо в границю та обчислюємо
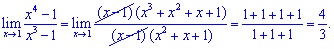
Границя функції рівна 4/3.
Завдання 4. Знайти похідну 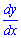 функції
функції
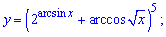
Розв'язання: Знаходимо похідну за правилом складеної функції. Спершу від степеневої функції за формулою
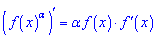
а далі від фукцій в дужках.
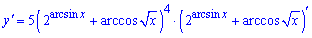
В останній дужці похідну шукаємо від кожного доданку окремо.
До першого доданку застосовуємо логарифмічне диференціювання
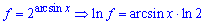
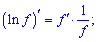
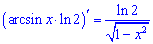
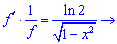
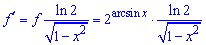
Другий доданок внесе такий вклад
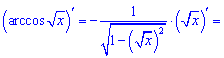
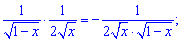
Підставляємо знайдені значення в похідну
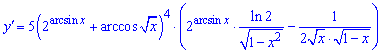
Даний приклад навчить Вас нових прийомів, тому добре в ньому розберіться.
Завдання 5. Дослідити функцію z=f(x,y) на екстремум:
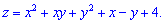
Розв'язання: Методика дослідженя функції двох змінних на екстремум наступна.
Знаходимо похідні dz/dx і dz/dy та пирівнюємо їх до нуля.
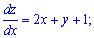
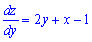
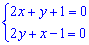
Розв'язавши систему рівнянь знайдемо екстремальну точку.
З другого рівняння виражаємо невідому х та підставляємо в перше.
х=1-2y
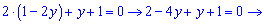
3-3y=0 y=1.
y=1.
Знайдене значення підставляємо в будь-яке із рівнянь (2)

Отже точка А(-1;-1) точка екстремуму.
Знайдемо другі похідні
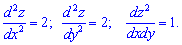
За необхідною ознакою екстремуму знаходимо
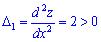
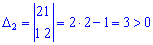
Оскільки обидва додатні 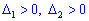 , то точка А(-1;1)є точкою мінімуму.
, то точка А(-1;1)є точкою мінімуму.
Графічно функції в околі мінімуму зображено нижче
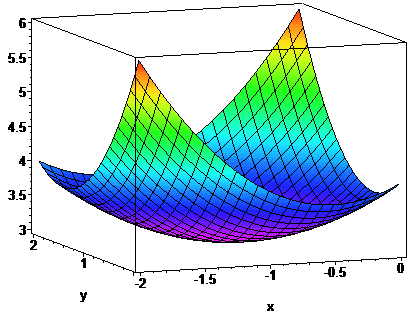
Завдання 6. Знайти невизначені інтеграли:
а) 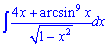
Розв'язання: Розбиваємо підінтегральний вираз на два доданки та знаходимо невизначені інтеграли. Перший інтеграл знаходимо заміною змінних, другий - внесенням змінної під диференціал.
1) 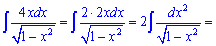
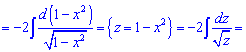
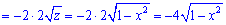
2) 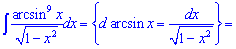
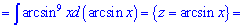
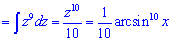
Сумуємо інтеграли

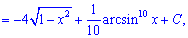
де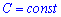 - константа. На цьому всі розрахунки.
- константа. На цьому всі розрахунки.
б) 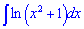
Розв'язання: Даний інтеграл обчислюємо за правилом інтегрування частинами udv
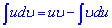
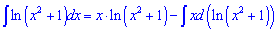
Знаходимо інтеграл, що залишився
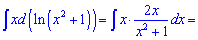
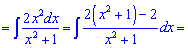
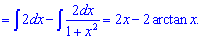
Підставляємо вираз у вихідний інтеграл
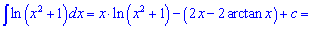
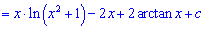
У відповіді отримали і логарифм і арктангенс.
Завдання 7. Обчислити визначений інтеграл
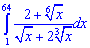
Розв'язання:Проведемо деякі перетвореня підінтегральної функції
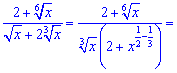
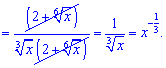
після чого виконаємо інтегрування
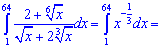
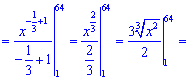
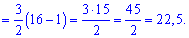
Інтеграл рівний 22,5.
Завдання 8. Обчислити площу фігури, обмеженої лініями:
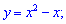
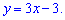
S-?
Розв'язання: Знайдемо точки перетину цих ліній
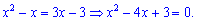
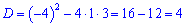
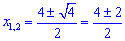
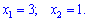
Для з'ясування, яка крива знаходиться вище на графіку, а яка нижче підставляємо точку з проміжку [1;3], наприклад візьмемо точку х=2
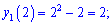
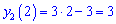
Обидві функції на графіку матимуть такий вигляд
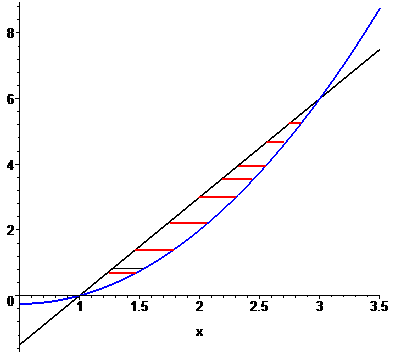
Отже друга лінія вище на графіку від першої, враховуючи це знаходимо площу
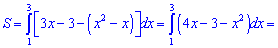
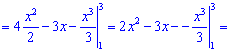
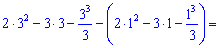
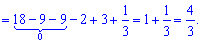
Якщо не враховувати порядку кривих то може вийти від'ємне значення інтегралу. Пам'ятайте, що площа від'ємною не буває (міняйте знак при відповіді).
Вибирайте для себе простіші та швидкі методи обчислення тих чи інших завдань. Практикуйте та не майте труднощів у подібних обчисленнях.
Приклад 1. Обчислити границю
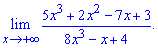 Розв'язання: В границі змінна прямує до безмежності, тому в дробовій функції з чисельника і знаменника виносимо змінну в старшому степені та обчислюємо границю
Розв'язання: В границі змінна прямує до безмежності, тому в дробовій функції з чисельника і знаменника виносимо змінну в старшому степені та обчислюємо границю
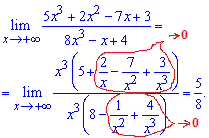
Тут враховано, що доданки в чисельнику і знаменнику, що містять ділення на змінну в 1, 2, 3 степені прямують до нуля при змінній прямуючій до безмежності. Таким чином границя рівна 5/8.
Приклад 2. Обчислити границю
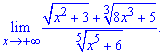 Розв'язання: Маємо невизначеність типу безмежність поділити на безмежність
Розв'язання: Маємо невизначеність типу безмежність поділити на безмежність 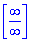 .
.
Винесемо з чисельника і знаменника змінну х
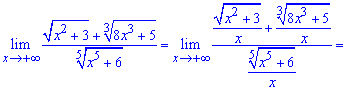
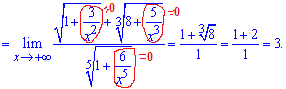
Тут також враховано, що деякі доданки під коренем прямують до нуля холи "ікс" прямує до безмежності.
Приклад 3. Обчислити границю
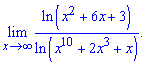 Розв'язання: Маємо границю у вигляді частки логарифмів, яка при підстановці дає невизначеність типу безмежність поділити на безмежність
Розв'язання: Маємо границю у вигляді частки логарифмів, яка при підстановці дає невизначеність типу безмежність поділити на безмежність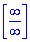 . Зробимо наступне перетворення, в чисельнику в логарифмі виділимо множником "ікс" в квадраті, в знаменнику "ікс " в 10 степені та перетворимо згідно властивостей логарифма
. Зробимо наступне перетворення, в чисельнику в логарифмі виділимо множником "ікс" в квадраті, в знаменнику "ікс " в 10 степені та перетворимо згідно властивостей логарифма
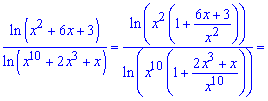
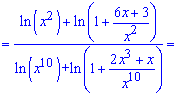
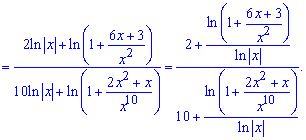
Застосовуючи співвідношення для нескінченно великих функцій і для обчислення границь, отримаємо
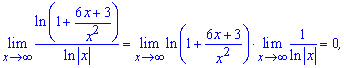
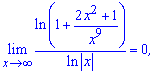
звідси, знаходимо кінцевий вигляд границі
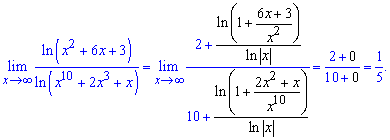
Границя функції рівна 0,2.
Приклад 4. Обчислити границю
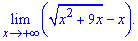 Розв'язання: Маємо невизначеність типу безмежність розділити на безмежність
Розв'язання: Маємо невизначеність типу безмежність розділити на безмежність 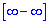 .
.
Функція має вигляд корінь мінус змінна. Щоб позбутися невизначеності помножимо і розділимо на спряжену функцію
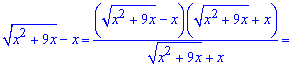
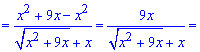
та спростимо чисельник і знаменник на "ікс"
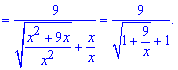
Отримали компактний вираз функції для знаходження границі
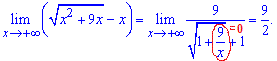
Границя функції рівна 4,5.
Приклад 5. Знайти границю
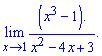 Розв'язання: Маємо частку функцій, які дають невизначеність типу нуль поділити на нуль
Розв'язання: Маємо частку функцій, які дають невизначеність типу нуль поділити на нуль  . В околі точки х=1 розкладемо функції чисельника і знаменника
. В околі точки х=1 розкладемо функції чисельника і знаменника
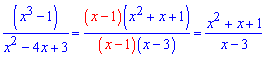
та спростимо на множник, що вносить особливість в границю. Границя функції зведеться до вигляду
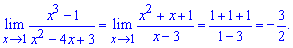
В результаті отримаємо -1,5.
Приклад 6. Обчислити границю
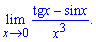 Розв'язання: В чисельнику маємо тангенс і синус, в знаменнику "ікс" в кубі. При підстановці отримаємо невизначеність типу нуль поділити на нуль
Розв'язання: В чисельнику маємо тангенс і синус, в знаменнику "ікс" в кубі. При підстановці отримаємо невизначеність типу нуль поділити на нуль  .
.
Винесемо в чисельнику тангенс за дужки та скористаємося формулами для обчислення границь нескінченно малих функцій
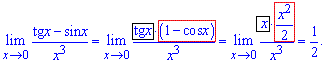
Границя рівна 0,5.
Приклад 7. Обчислити границю
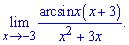 Розв'язання: Знову маємо невизначеність типу нуль поділити на нуль
Розв'язання: Знову маємо невизначеність типу нуль поділити на нуль  .
.
Функція арксинус прямує до нуля при змінній, яка прямує до (-3). Тому застосувавши нескінченно малі функції знайдемо границю
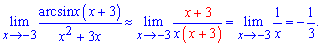
Приклад 8. Знайти границю
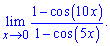 Розв'язання: Оскільки косинуси в чисельнику і знаменнику прямують до одиниці коли "ікс" прямує до нуля, то маємо невизначеність виду нуль поділити на нуль. За правилом еквівалентних нескінченно малих функцій замінимо чисельник і знаменник розкладом в околі нуля перших членів ряду
Розв'язання: Оскільки косинуси в чисельнику і знаменнику прямують до одиниці коли "ікс" прямує до нуля, то маємо невизначеність виду нуль поділити на нуль. За правилом еквівалентних нескінченно малих функцій замінимо чисельник і знаменник розкладом в околі нуля перших членів ряду
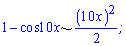
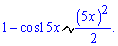
Відшукання границі спроститься до частки
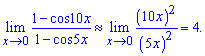
На цьому контрольна робота на знаходження границь функцій розв'язана. Більше завдань на границю Ви можете знайти в категорії "Обчислення границь" з меню вищої математики.
Сподіваюсь приклади на границі були корисними для Вас та частині стануть підказкою на контрольній роботі чи тестах.
Завдання: 1.3 Обчислити суму рядів:
а)
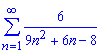
Розв'язання: Спершу виконуємо перевірку ряду на збіжність
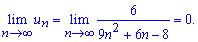
Границя загального члена ряду рівна нулю, отже даний ряд збігається. Якщо Ви отримаєте границю відмінну від нуля, хоча і скінченну, то такий ряд буде розбіжним, а його сума рівна плюс або мінус безмежності. Тобто такі ряди не сумують. На екзаменах, як правило такі приклади не зустрічаються, однак на тестах можливо все. Тому перш ніж переходити до сумування ряду перевіряйте його на збіжність.
Напряму Ви суму цього ряду оцінити не зможете, єдиний вихід розкласти знаменник загального члена ряду на прості множники, а далі методом невизначених коефіцієнтів сам дріб звести до різниці найпростіших дробів
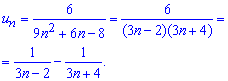
Це дасть можливість звести обчислення суми ряду до відшукання різниці двох рядів
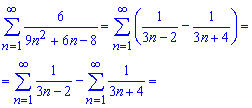
Якщо останні розписати в явному вигляді, то завжди отримаєте, що більшість доданків при обчисленні дасть нуль (підкреслені). Решта, що залишилися (виділені чорним) і є шуканою сумою ряду
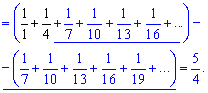
Тепер Ви на крок ближче, щоб самостійно знайти суму ряду.
б) 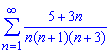
Розв'язання: Знаходженням границі
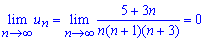
переконуємося, що вона рівна 0, а заданий ряд збігається.
Далі методом невизначених коефіцієнтів розкладаємо загальний член ряду на прості дроби
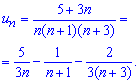
Це дозволяє перейти від обчислення суми 1 складного ряду до сумування 3 простих рядів
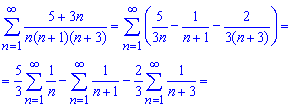
Ряди записуємо у явному вигляді і виділяємо доданки, що знищаться при сумуванні
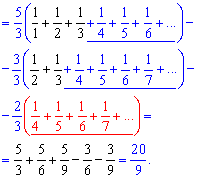
Підказкою слугує те, що члени одного з рядів (виділений червоним) в кінцеву суму жодного вкладу не внесуть. Також для зручності обчислень записуйте ряди один під одним. Для чого це потрібно Ви можете бачити з цього прикладу.
Завдання: 2.4 Дослідити збіжність рядів:
а) 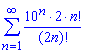
Розв'язання: Заданий ряд має додатні члени, тому можемо дослідити збіжність ряду за ознакою Даламбера:
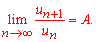
Записуємо члени ряду, що фігурують в границі
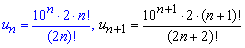
та підставляємо у формулу Даламбера
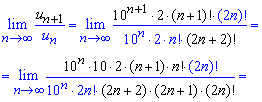
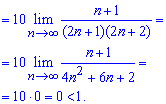
При розписуванні границі найбільше помилок в студентів виникає при розписуванні факторіалів, тому добре вивчіть властивості факторіалів.
Оскільки границя менша одиниці A=0<1, то даний ряд збігається!
б) 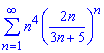
Розв'язання: Досліджувати на збіжність ряд будемо за ознакою Даламбера. Для цього записуємо формули загального члена ряду та наступного після нього
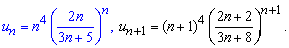
Далі підставляємо їх у границю та, наскільки це можливо, спрощуємо її
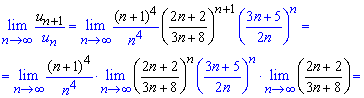
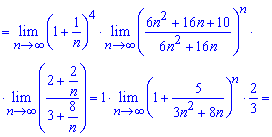
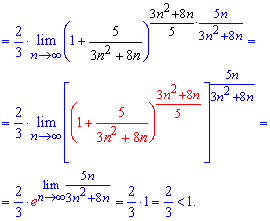
При обчисленні один з множників під границею рівний другій чудовій границі – експоненті.
Оскільки границя менша одиниці A=2/3<1, то робимо висновок про збіжність ряду.
Завдання: 3.5 Знайти радіус збіжності та область збіжності степеневих рядів:
а) 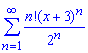
Розв'язання: Заданий функціональний ряд може при певних значеннях змінної приймати від'ємні значення, тому для дослідження збіжності ряду за ознакою Даламбера
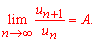
складемо ряд із модулів членів заданого ряду
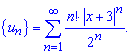
Записуємо загальний та наступний після нього члени ряду з модулів
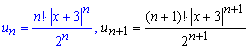
та підставляємо їх у границю
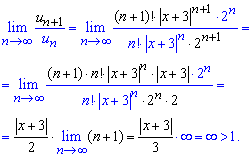
Розписавши факторіали та степеневі залежності, прийдемо до залежності, яка не є обмеженою. Границя рівна безмежності, отже функціональний ряд розбігається (за теоремою Даламбера) при всіх дійсних значеннях змінної 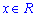 .
.
Це означає, що радіус збіжності рівний нулю R=0, а область збіжності порожня множина 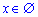 .
.
б) 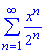
Розв'язання: Складемо ряд із модулів членів заданого ряду:
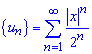
а далі виконуємо дослідження ряду на збіжність за теоремою Даламбера.
Знаходимо границю частки старшого та молодшого членів функціонального ряду
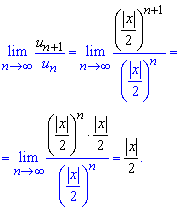
За теоремою Даламбера ряд збігається для змінних, що задовільняють умову
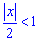 .
.
Розкриваючи модуль знаходимо 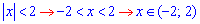 область збіжності ряду та записуємо радіус збіжності R=2.
область збіжності ряду та записуємо радіус збіжності R=2.
Завдання: 4.6 Розкласти дробову функцію в ряд по степенях x:
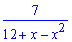
Розв'язання: Розкладемо функцію методом невизначених коефіцієнтів на суму простих дробів, а далі перетворимо знаменники, щоб мати зручний запис для розкладу
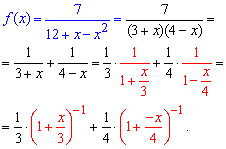
Функцію f(x) розкладемо в ряд за степенями x, скориставшись формулами Маклорена для степеневих функцій:
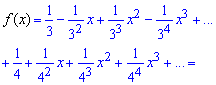
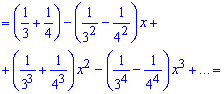
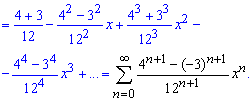
Вкінці згрупуємо доданки при однакових степенях "ікс" та розклад функції записуємо рядом.
Завдання: 5.7 Розкласти арктангенс функцію в ряд по степенях x:
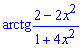
Розв'язання: Для розкладу арктангенса застосуємо наступну методику. Спершу знайдемо похідну складеної функції від арктангенса
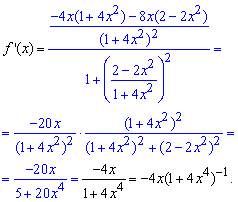
Розкладемо похідну арктангенса в ряд за степенями x, використовуючи формули Маклорена
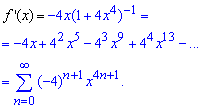
Щоб отримати розлад арктангенса інтегруємо похідну. Враховуючи, що f(0)=arctg(2), отримаємо ряд за степенями x заданої функції f(x):
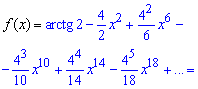
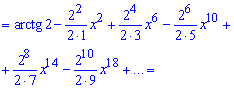
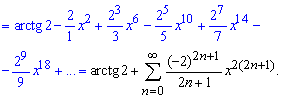
Останній перехід до ряду не такий очевидний, однак для знакозмінного ряду саме такі залежності отримують у відповідях.
Завдання: 6.8 Розкласти функцію в тригонометричний ряд Фур'є:
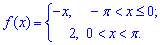
Розв'язання:Схема розкладу в ряд Фур'є детально розписана в попередніх статтях. Тут інтегруванням визначаємо коефіцієнти Фур'є:
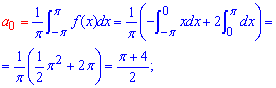
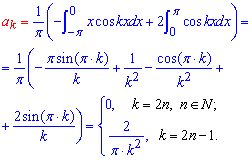
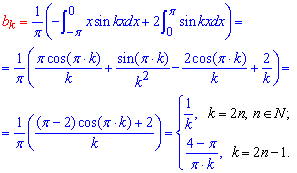
Далі для заданої функції ряд Фур'є відповідно до формул матиме вигляд
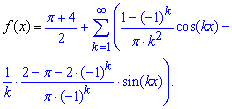
В кінцевому розкладі функції коефіцієнти Фур'є для непарних та парних індексів об'єднали в один. В цьому, як і в інтегруванні вся суть розкладу функції в тригонометричний ряд. Ось такі завдання з теорії рядів Вам доведеться вирішувати на контрольній чи екзаменах. Якщо сумніваєтеся у власних силах, то замовляйте обчислення у нас!