Шановні школярі, випускники, абітурієнти, цей розділ допоможе підготуватися до зовнішнього незалежного оцінювання з математики 2017 року. Відповіді до тестів допоможуть засвоїти теоретичний матеріал та методику обчислень, систематизувати та підвищити накопичений рівень знань з математики. Відповіді до прикладів з математики будуть цікаві для школярів 9, 10, 11 класів, а також їх батьків.
Розділ V. Планіметрія
Задача 5.1 - 5.32 мають по п'ять варіантів відповідей, із яких тільки одна правильна. Правильно виконане завдання оцінюється 1 балом.
Задача 5.30 Вкажіть кількість осей симетрії правильного шестикутника. 
Розв'язання: Побудуємо шестикутник та зобразимо осі симетрії. 
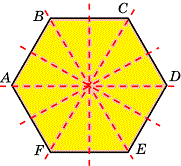Отримаємо 3 осі симетрії по вершинах шестикутника та 3 осі симетрії через середини сторін. Сумуємо осі
3+3=6.
Варіант В містить правильну відповідь до тесту.
Відповідь: В.
Задача 5.31 Дано паралелограм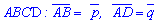 
. Точка L ділить сторону АВ у відношенні 2:1, а точка К - сторону DС у відношенні 1:2. Виразіть вектор 
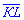через вектори 
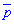і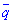 
. 
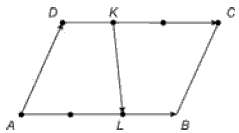
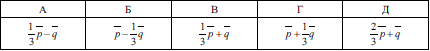Розв'язання: Щоб розв'язати задане та подібні завдання необхідно знати дві формули, а вірніше запам'ятати зображений нижче рисунок. 
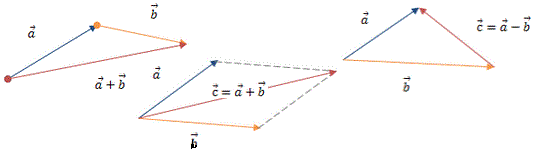Сумою векторів є більша діагональ паралелограма, побудована на векторах, а різницею – менша проведена від вершини вектора, який віднімаємо до вершини другого, від якого віднімаємо.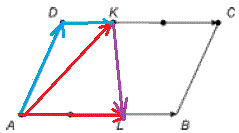 
Знаючи це спочатку виразимо вектор АК
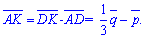
За побудовою обчислюємо шуканий вектор
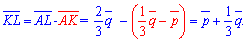
Ось так просто можна вирішувати задачі на вектори любої складності, якщо добре знати теорію. Варіант Г може принести 1 бал на ЗНО тестуванні.
Відповідь: Г.
Задача 5.32 Многокутник, зображений на рисунку, складено з чотирьох рівних квадратів. Знайдіть площу многокутника, якщо його периметр дорівнює 20 см.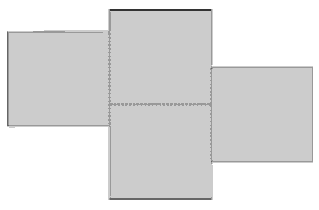
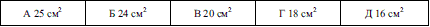Розв'язання: Периметр рівний довжині контуру. Знайдемо всі спільні сторони перетину квадратів з многокутником, причому вони віднімають двократний розмір від периметра. Отримаємо 2 сторони по 2 плюс 2 між центральними квадратами. Сумарна кількість сторін квадратів, які утворюють периметр многокутника рівна
(4*4-2*3)*x=(16-6)*x=10*x.
Складаємо рівняння
10*х=20; х=20/10=2.
Площа многокутника рівна площі чотирьох квадратів
S=4*2*2=16 (сантиметрів квадратних).
Варіант Д тестових відповідей дозволить отримати потрібні бали.
Відповідь: Д.
Залишайтеся з нами і підготовка до ЗНО з математики залишиться для Вас приємним спогадом та зекономить багато часу та грошей на репетиторів.
Відповіді до ЗНО тестів
- ЗНО 2017 відповіді з математики
- Попередня стаття - ЗНО 2017 математика. Задачі на трикутники
- Наступна стаття - ЗНО 2017 математика. Задачі на площу фігур
