Розклад вектора за базисом

Означення базису, та що таке лінійно незалежні вектори пояснено в попередній публікації. Тут розглянемо розклад вектора за базисом на практиці.
Перший приклад відповідає розкладу вектора в декартовій площині (через 2 вектори), всі наступні - в тримірному просторі (3 вектори).

ЗАВДАННЯ 1 Довести, що вектори a(1,3), b(2,5) утворюють базис та розкласти вектор C(0,1) за цим базисом.
Розв'язання: Доведення досить просте, з векторів a,b утворюємо матрицю та знаходимо її визначник.
Так як перевіряємо на базис вектори в декартовій системі координат то знайти визначник матриці 2 порядку перехресним множенням не пробема

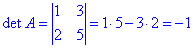
Детермінант DetA=-1 – не рівний нулю, отже вектори лінійно незалежні (утворюють базис).
Знайдемо розклад С через a, b.
C=x*a+y*b
або
0=x+2y;
1=3x+5y.
З першого рівняння виражаємо x та підставляємо в друге
x=-2y;
3(-2y)+5y=1;
-y=1->y=-1;
x=-2y=-2*(-1)=2.
Підставляємо в рівняння розкладу С=2a-b.
На цьому приклад розв'язано, далі переходимо до тримірного простору.

ЗАВДАННЯ 2 Довести, що вектори 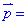(0,1,2), 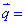(1,0,1), 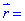(-1,2,4) утворюють базис та розкласти вектор 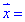(-2,4,7) за цим базисом.
Розв'язання: Доведення, що вектори утворюють базис через ранг або визначник наведено в попередній публікації. Причому номери завдань співпадають.
Тут будемо пояснювати методику розклад векторів у базисі, а вона досить проста:
координати вектора 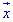в базисі 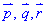запишемо через лінійну комбінацію векторів:

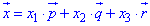
Це векторна форма запису. Дане рівняння перетворюємо до координатного запису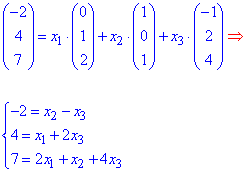

Далі кожен рядок записуємо у вигляді рівняння, таким чином отримуємо систему трьох рівнянь з трьома невідомими.
Розв'яжемо цю систему лінійних алгебраїчних рівнянь методом Гауса:

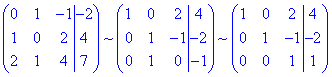
звідси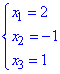
– координати вектора в базисі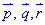
Тому розклад вектора за цим базисом наступний:

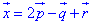
ЗАВДАННЯ 3 Довести, що вектори (5,1,0), (2,-1,1), (1,0,-1) утворюють базис та розкласти вектор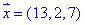за цим базисом.
Розв'язання: Розкладемо вектор 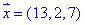за цим базисом.

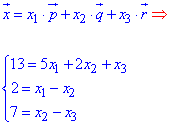
Розв'яжемо цю систему лінійних алгебраїчних рівнянь методом Гауса:

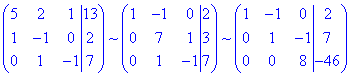
звідси
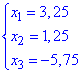– координати вектора в базисі, тому отримаємо розклад вектора за цим базисом:

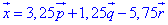
ЗАВДАННЯ 4 Розкласти вектор (-2,4,7) за базисом (0,1,2), (1,0,1), (-1,2,4).
Розв'язання: Знайдемо розклад вектора (-2,4,7) за наведеним базисом.

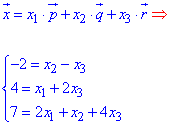
Розв'яжемо систему лінійних алгебраїчних рівнянь (СЛАР) методом Гауса: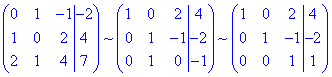

З останньої системи зворотнім ходом визначаємо координати

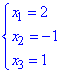
та записуємо розклад вектора в базисі:

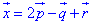
ЗАВДАННЯ 5 Знайти розклад вектора (-9,5,5) в базисі (4,1,1), (2,0,3), (-1,2,1).
Розв'язання: Записуємо загальну формулу вектора через лінійну комбінацію трьох векторів: .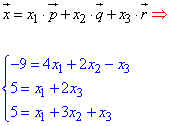

Систему рівнянь обчислюємо методом Гауса:

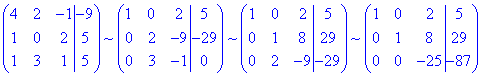
Розв'язок СЛАР

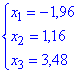
Підставляємо "ікси" в розклад вектора за базисом:

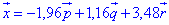
ЗАВДАННЯ 6 Довести, що вектори (1,0,2), (0,1,1), (2,-1,4) утворюють базис та розкласти вектор (3,-3,4) за цим базисом.
Розв'язання: Лінійну комбінацію векторів записуємо у вигляді системи рівнянь

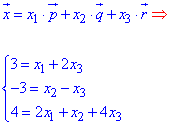
Її можна розв'язувати методом Крамера, атричним методом, але враховуючі прості числа та багато нулів, найкраще підходить метод Гауса:

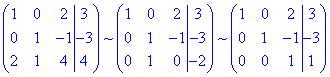
З останнього рівняння знаходимо 3 невідому і так по східцях до 1 рівняння знаходимо всі 3

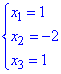
Вкінці записуємо розклад вектора:

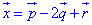
ЗАВДАННЯ 7 Довести, що вектори (1,0,5), (-1,3,2), (0,-1,1) утворюють базис та розкласти вектор (5,15,0) за базисом.
Розв'язання: Представимо вектор (5,15,0) у вигляді лінійної комбінації векторів базису. Далі її записуємо у вигляді СЛАР

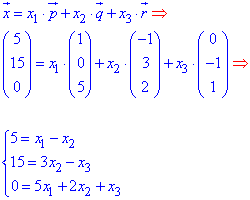
Розв'язуємо систему лінійних алгебраїчних рівнянь методом Гауса:

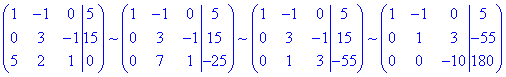
звідси значення коефіцієнтів наступні

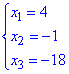
Сам розклад вектора 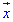рівний:

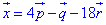
ЗАВДАННЯ 8 Знайти розклад вектора (2,-1,11) за векторами базису a(1,1,0), b(0,1,-2), c(1,0,3).
Розв'язання: Розкладемо вектор x(2,-1,11) за базисом a,b,c.

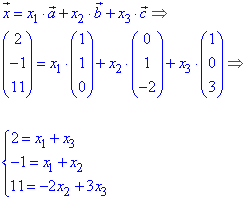
Систему лінійних алгебраїчних рівнянь розв'яжемо методом Гауса:

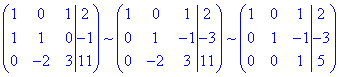
звідси з останнього рівняння до першого знаходимо x_i
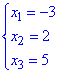– координати вектора 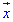в базисі .
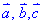Векторний запис розкладу має вигляд:

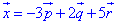
Як Ви бачите приклади не складні і по суті зводяться до розв'язування систем рівнянь другого, третього порядку.
Такі задачі під силу виконати кожному студенту, тож не лінуйтеся та практикуйте самостійно!