Всі студенти та викладачі ВУЗів, що шукають інформацію "Як обчислювати рівняння на повний диференціал?" з цього уроку отримають повну інструкцію та в додаток готові приклади. Спершу коротке ознайомлення - що таке рівняння в повних диференціалах? Як обчислювати рівняння на повний диференціал?
Далі розбір готових прикладів, після яких можливо у Вас не залишиться питань по даній темі.
Рівняння в повних диференціалах
Означення 1. Рівняння вигляду M(x,y)dx+N(x,y)dy=0 називається рівнянням в повних диференціалах , якщо залежність перед знаком рівності є повним диференціалом деякої функції двох змінних u(x,y), тобто справедлива формула
du(x,y)=M(x,y)dx+N(x,y)dy. (1)
Таким чином, початкове рівняння за змістом означає рівність нулю повного диференціалу функції du(x,y)=0.
Інтегруючи диференціал отримаємо загальний інтеграл ДР у вигляді
u(x,y)=С. (2)
При обчисленнях, як правило, сталу покладають рівною нулю.
Пред обчисленнями завжди постає питання, як перевірити, що задане ДР є рівнянням в повних диференціалах. На це питання дає відповідь наступна умова.
Необхідна і достатня умова повного диференціалу
Необхідною і достатньою умовою повного диференціала є рівність між собою частинних похідних
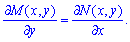 (3)
(3)
При розв'язанні диференціальних рівнянь її перевіряють в першу чергу, щоб ідентифікувати чи маємо рівняння в повних диференціалах, чи можливо інше.
За змістом ця умова означає, що мішані похідні функції рівні, тобто враховуючи залежності
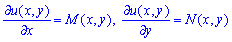 (4)
(4)
необхідну і достатню умову існування повного диференціалу можемо записати формулою
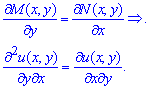
Наведений критерій і застосовують при перевірці рівняння відповідності повному диференціалу, хоча при вивченні даної теми викладачі не зададуть Вам іншого типу рівнянь.
Алгоритм розв'язання рівняння в повних диференціалах
З позначень (4) часткових похідних повного диференціалу функції u(x,y) слідує, що її можемо знайти інтегруванням
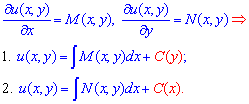
Ці формули дають вибір при обчисленнях, тому для інтегрування вибирають ту часткову похідну, інтеграл від якої легше знайти на практиці.
Далі другий важливий момент – невизначений інтеграл являє собою первісну, тобто "+С", яку слід визначити.
Тому, якщо інтегруємо часткову похідну M(x,y) по "ікс" то стала залежить від "ігрик" і навпаки – якщо інтегруємо N(x,y) по "ігрик" то стала залежна від "ікс".
Далі, щоб визначити сталу беруть похідну від u(x,y) по іншій змінній ніж та, що використовували при інтегруванні і прирівнюють до другої часткової похідної.
В формулах це матиме запис
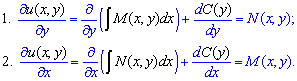
Як правило деякі доданки спрощуються і отримаємо рівняння на похідну сталої. Для (1) з рівнянь матимемо
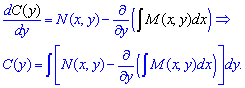
Остаточно, загальний інтеграл після визначення сталої має вигляд
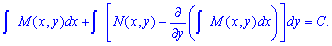
В симетричній формі отримаємо відповідь і для іншого рівняння.
Запис тільки на вигляд складний, насправді на практиці все виглядає значно простіше і зрозуміліше. Проаналізуйте наступні завдання на повні диференціали.
Готові відповіді на рівняння в повних диференціалах
Приклад 1. (6.12) Знайти загальний інтеграл диференціального рівняння:
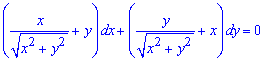
Розв'язання:Ліва частина рівняння є повним диференціалом деякої функції 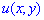 , оскільки виконується умова
, оскільки виконується умова
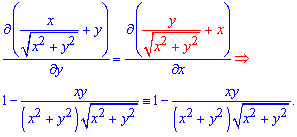
Звідси записуємо часткову похідну функції двох змінних від "ікс"
![]()
та інтегруванням знаходимо її вигляд
![]()
Щоб довизначити сталу знаходимо часткову похідну функції по "ігрику" та прирівнюємо зі значенням в рівнянні
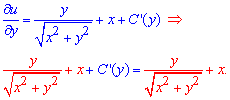
Подібні доданки в правій і лівій частині скорочуємо, після чого сталу знаходимо інтегруванням
![]()
Тепер маємо всі величини для запису загального інтегралу диференціального рівняння у вигляді
![]()
Як можна переконатися, схема розв'язування рівнянь в повних диференціалах не важка і її під силу освоїти кожному. Важливе значення мають множники при диференціалах, оскільки їх доводиться інтегрувати та диференціювати, щоб знайти розв'язок.
Приклад 2. (6.18) Знайти загальний інтеграл диференціального рівняння
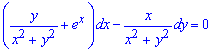
Розв'язання: За теорією ліва частина рівняння повинна бути повним диференціалом деякої функції двох змінних u(x,y), при цьому перевіряємо чи виконується умова
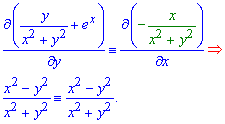
Звідси записуємо часткову похідну та через інтеграл знаходимо функцію
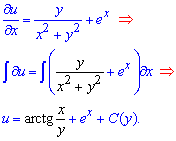
Обчислюємо часткову похідну функції двох змінних по y та прирівнюємо до правої сторони диференціального рівняння.
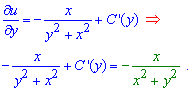
Похідна виражається залежністю
![]()
З врахуванням сталої отримали загальний інтеграл диференціального рівняння у вигляді
![]()
На цьому обчислення даного прикладу завершено.
Приклад 3. (6.20) Знайти загальний інтеграл диференціального рівняння:
![]()
Розв'язання: Ліва частина рівняння буде повним диференціалом деякої функції двох змінних u(x; y) , якщо виконуватиметься умова
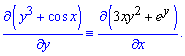
Звідси починаємо розв'язування рівняння, а вірніше ітегрування одної з часткових похідних
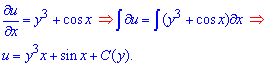
Далі знаходимо похідну від отриманої функції по змінній y та прирівнюємо до правої сторони диференціальної залежності
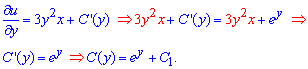
Це дозволяє знайти константу, як функцію від y. Якщо починати розкривати диференціальну залежність з правої сторони, то отримали, що константа залежить від x. Загальний розв'язок диференціального рівняння при цьому не зміниться і для заданого рівняння має вигляд
![]()
На цьому приклад розв'язано.
Приклад 4. (6.21) Знайти загальний інтеграл диференціального рівняння:
![]()
Розв'язання: Перевіряємо чи є повним диференціалом деякої функції u(x,y) вираз, що прирівнюється до нуля
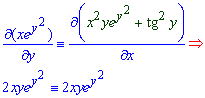
Виписуємо часткову похідну функції двох змінних та інтегруванням відновлюємо розв'язок
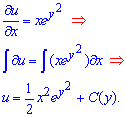
Далі уточнюємо сталу. Для цього обчислюємо похідну функції по y та прирівнюємо до значення в рівнянні (виділено зеленим)
![]()
![]()
Звідси, виражаємо похідну інтегруванням
![]()
Загальний розв'язок диференціального рівняння маємо право записати формулою
![]()
Для закріплення тематики просимо самостійно перевірити, що дані рівняння є рівняннями в повних диференціалах, і розв’язати їх:
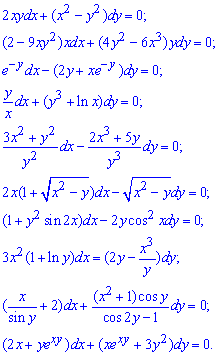 Тут Вам і кореневі функції, тригонометричні, експоненти, логарифми, одним словом - все що може чекати Вас на модулях та екзаменах.
Тут Вам і кореневі функції, тригонометричні, експоненти, логарифми, одним словом - все що може чекати Вас на модулях та екзаменах.
Після цього Ви повинні навчитися розв'язувати такого типу рівняння. З наступної статті Ви познайомитеся з рівняннями вигляду
M(x,y)dx+N(x,y)dx=0
які достатньо подібні до рівнянь в повних диференціалах, проте не виконується умова рівності часткових похідних. Їх обчислюють пошуком інтегруючого множника, домножуючи на який наведене рівняння стає рівнянням в повних диференціалах.


