В попередній статті наведені основні теоретичні відомості, які дають відповіді на питання "Що таке однорідне диференціальне рівняння?", "Як його ідентифікувати серед інших ДР?", "Яка заміна змінних дозволяє однорідне ДР звести до рівняння з відокремленими змінними?" і тому подібні. Тому хто не володіє основами рекомендуємо переглянути попередній матеріал. Також наведено відповіді до трьох прикладів, які лише ознайомлюють з методами отримання загального інтегралу таких ДР.
Далі будуть проаналізовані непрості з точки зору обчислень однорідні ДР, які містяться в збірнику задач з курсу «Диференціальні рівняння», (Бокало М. М.).
Тому уважно розбирайте всі перетворення та заміни, що описані у формулах переходу від одного р-ня до іншого ДР, оскільки описати все та зробити наголоси на дрібних речах не завжди є можливо.
Методика обчислення однорідних диференціальних рівнянь
Приклад 2.60 Знайти загальний інтеграл диференціального рівняння
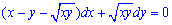
Розв'язання: З вигляду р-ня бачимо, що ніяким чином його не можна звести до диференціального рівнянь з відокремленими змінними, оскільки маємо попарні добутки змінних.
Але бачимо, що функці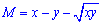ї 
і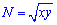 
- є однорідними функціями першого степеня.
Тому поділимо рівняння на x (зауважимо, що змінну можна представити у вигляді добутку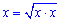 
) :
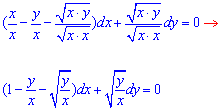
зробимо заміну змінних y=z*x, тоді dy=x*dz+z*dx,
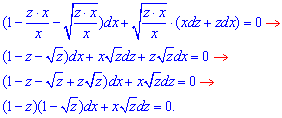
Отримали диференціальне рівняння з відокремлюваними змінними:
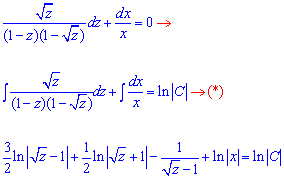
далі зробимо елементарні перетворення, використовуючи властивості логарифмічної, степеневої і показникової функції:
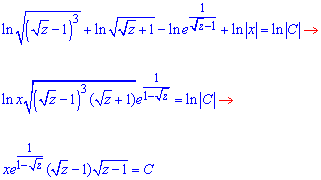
Повернемося до початкових змінних (z=y/x):
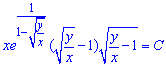
далі знову спростимо вираз
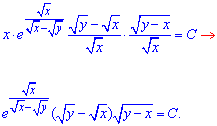
Крім цього, розв'язками заданого диференціального рівняння можуть знаходитись серед виразів, на які ми ділили, тобто x=0, 1-z=0 і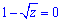 
.
Але при C=0 розв'язок вже містить 1-z=0 і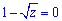 
звідки
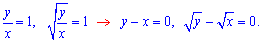
Тому отримали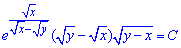 
- загальний інтеграл рівняння і x=0 - особливий розв'язок.
-------------------------------------------------
Вище мали інтеграл (*), його обчислення наведено далі:
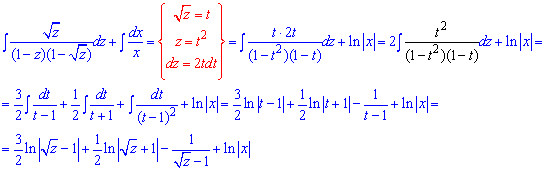
Дріб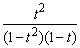 
розклали методом невизначених коефіцієнтів:
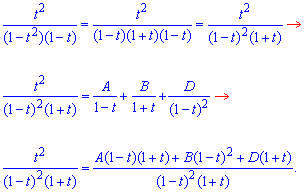
t2=A-At2+B-2Bt+Bt2+D+Dt,
1*t2+0*t+0=(-A+B)t2+(-2B+D)t+(A+B+D),
прирівнюємо коефіцієнти при однакових степенях t, та розв'язуємо систему рівнянь, отримаємо A=-3/4, B=1/4, D=1/2.
Звідки отримаємо наступний розклад дробу на прості множники
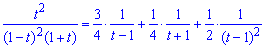
На цьому і всі розрахунки до заданого прикладу.
Приклад 2.65 Знайти розв'язок диференціального рівняння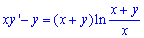
Розв'язання: Поділимо ДР на змінну х
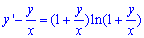
далі робимо заміну y=z*x, тоді y'=z'*x+z,
z'*x+z-z=(1+z)ln(1+z).
Переходимо до ДР з відокремленими змінними та виконуємо інтегрування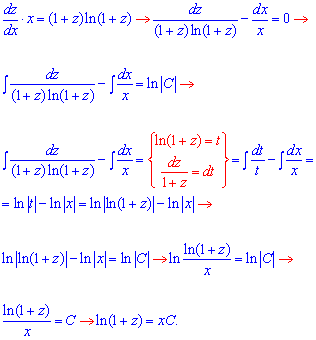
Повернемося до початкових змінних: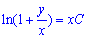 
- загальний інтеграл рівняння.
Приклад 2.72 Розв'язати диф. р-ня
(13x+y)dx+(y-5x)dy=0
Розв'язання: Ділимо на аргумент, щоб переконатися що маємо однорідне диф. р-ня
(13+y/x)dx+(y/x-5)dy=0,
а далі виконуємо заміну змінних y=z*x, тоді dy=x*dz+z*dx,
(13+z)dx+(z-5)(x*dz+z*dx),
13dx+z*dx+zx*dz-5x*dz+z2dx-5z*dx=0 ,
x(z-5)dz+(z2-4z+13)dx=0.
Розділяємо змінні та інтегруємо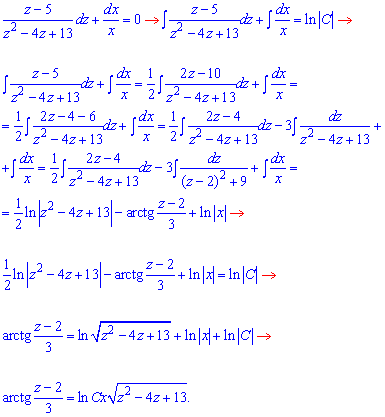
Отримали арктангенс та логарифм (за правилом суми логарифмів).
Повернемося до початкових змінних:
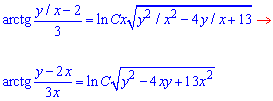- загальний інтеграл рівняння.
Приклад 2.59 Знайти загальний інтеграл диференціального рівняння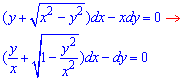
Розв'язання: Зробимо заміну змінних y=z*x, тоді dy=x*dz+z*dx,
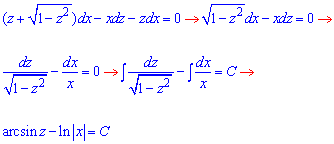
Повернемося до початкової заміни:
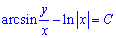
Врахуємо, що 1-z2=0 і x=0, звідси z=1,z=-1 і x=0.
Тому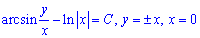 
- загальний розв'язок рівняння.
Приклад 2.81
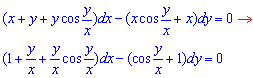
Розв'язання: Виконуємо заміну y=z*x, тоді dy=x*dz+z*dx,
(1+z+z*cos(z))dx-(cos(z)+1)( x*dz+z*dx)=0, відкриємо дужки і спростимо вираз:
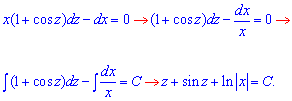
Повернемося до початкових змінних:
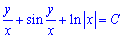- загальний інтеграл ДР.
Уважно перегляньте наступні приклади, а саме - схеми обчислення ДР,
можливо комусь вони допоможуть на практичних чи екзамені.
Приклад 2.94 Знайти загальний інтеграл диференціального рівняння
(2y-1)dx+(2x+y+1)dy=0,
Розв'язання: Складемо систему рівнянь і розв'яжемо її:
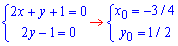
звідси
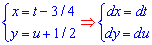
маємо
2u*dt+(2t+u)du=0,
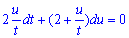
Зробимо заміну u=z*t, тоді z=u/t тоді
du=t*dz+z*dt, 2z*dt+(2+z)(t*dz+z*dt)=0,
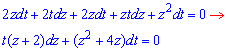
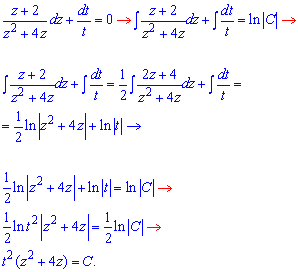
Повернемося до початкових змінних:
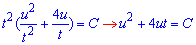
або u(u+4t)=C.
Оскільки t=x+3/4 і u=y-1/2, то (y-1/2)(y-1/2+4x+3)=C, або (2y-1)(8x+2y+5)=C - загальний інтеграл ДР.
Приклад 2.100 Знайти розв'язок диференціального рівняння
(1-2x-2y)dx+(3x+y-1)dy=0,
Розв'язання: Складаємо систему рівнянь і розв'язуємо її:
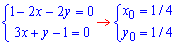
звідси
,
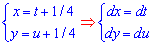маємо
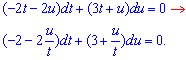
Робимо заміну u=z*t, тоді z=u/t, відповідно du=t*dz+z*dt,
(-2-2z)dt+(3+z)(t*dz+z*dt)=0,
t(3+z)dz+(z2+z-2)dt=0,
розділяємо змінні та інтегруємо диференціальне рівняння
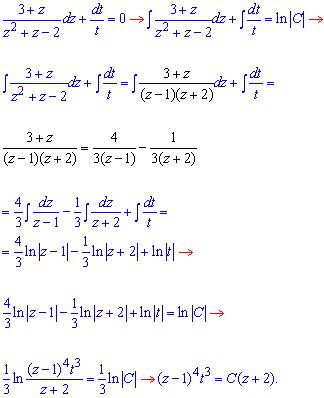
Повертаємося до початкової заміни:
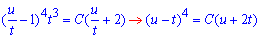
Оскільки t=x-1/4 і u=y-1/4, то (y-x)4=C(4y+8x-3).
Врахуємо, що z2+z-2=0 , z=1 і z=-2, тоді u=t, звідки x=y
(враховано при C=0)
u=-2t, звідки 4y+8x-3=0.
Тому (y-x)4=C(4y+8x-3) і (y-x)4=C(4y+8x-3) - загальні інтеграли рівняння.
Використана література:
- Збірник задач з курсу «Диференціальні рівняння». Бокало М. М. – Львів: Видавничий центр ЛНУ імені Івана Франка, 2014. – 179 с.
- Диференціальні рівняння. Бокало М. М. – Львів: Видавничий центр ЛНУ імені Івана Франка, 2014. – 232 с.
- Диференціальні рівняння в задачах: Навч. посібник / А. М. Самойленко, С. А. Кривошея, М. О. Перестюк. – К.: Либідь, 2003. – 504 с.
- Эльсгольц Л. Э. Дифференциальные уравнения и вариационное исчисление – 2-е изд. – Наука, 1969. – 424 стр. с илл.
