Задачі на рівнобедрений трикутник з розв'язками

Завдання на трикутники вимагають знання багатьох формул, без яких часто важко отримати правильну відповідь.
Тут наведені готові відповіді поширених на практиці прикладів, які вдалося знайти в збірниках тестів та шкільних підручниках. Не розглянутими лишилися важкі задачі, як, наприклад, застосування формули Герона, чи знаходження певних геометричних розмірів. В скорому часі і вони будуть детально розписані та пояснені.

ЗАДАЧА 1 Основа рівнобедреного трикутника рівна 24 см. Знайдіть радіус кола, вписаного в трикутник, якщо проведена до основи висота рівна 16 см.
Розв'язання: З курсу геометрії відомо, що радіус вписаного у трикутник кола рівний відношенню його площі до півпериметра. Залишилося знайти значення останніх двох величин.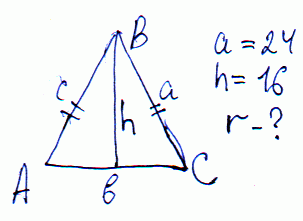

Площа трикутника за найпоширенішою формулою рівна половині добутку основи на висоту, проведеної до неї. Виконуємо обчислення
S= 24*16/2=192 (кв. см.)
Для визначення периметру нам потрібно відшукати довжину бічної сторони.
У рівнобедреному трикутнику висота, проведена до основи в, є бісектрисою і медіаною.
За теоремою Піфагора знаходимо бічну сторону трикутника
b=sqrt(16²+(24/2)²)=20 (cм)
Периметр - сума всіх сторін
P= 2*20+24=64 (см)
Знаходимо радіус вписаного в трикутник кола за формулою
r=S/(2*P)=192/(64/2)=192/32=6 (см).

ЗАДАЧА 2 Основа рівнобедреного трикутника дорівнює 24 см бічна сторона 13 см. Обчисліть площу трикутника?
Розв'язання: Площа рівна пів добутку основи на висоту.

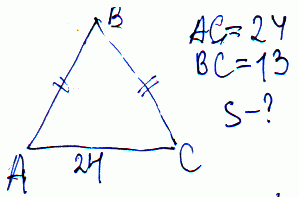
Основа нам відома, висоту знаходимо за теоремою Піфагора
h=√(b²-a²/4)= √(169-144)=5 (см).
Далі обчислюємо площу
S=a*h/2=24*5/2=60 (см. кв.)

ЗАДАЧА 3 З чотирьох рівних правильних трикутників склали трикутник. Обчисліть площу трикутника DЕF, якщо периметр трикутника АВС дорівнює 24 см.

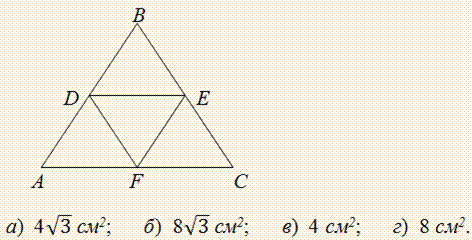
Розв'язання: Під правильним завжди розуміють рівносторонній трикутник.
Розділимо відомий периметр на трійку.
a=24/3=8 (см).
Так ми матимемо сторону великого трикутника. Далі є два шляхи, або шукати сторону малого трикутника і його площу. Або знайти площу великого трикутника і, за умовою, розділити на 4. Розглянемо другий варіант.
Висота трикутника за Піфагором рівна
h=√(8²-4²)=4√3 (см).
Знайдемо площу трикутника
S=8*4√3/2=16√3 (см. кв.).
Розділивши отримане значення на 4 дістанемо шукану площу трикутника
S1=4√3 (см. кв.)
Така відповідь відповідає першому номеру (а) тестових варіантів.

ЗАДАЧА 4 Діагональ, бічна сторона і більша основа рівнобедреної трапеції дорівнюють відповідно 40см, 13 см і 51 см. Знайдіть радіус кола, описаного навколо трапеції.
Розв'язання: Відома формула радіуса описаного кола навколо трапецї за сторонами і діагоналлю:
R=adc/4√p(p-a)(p-d)(p-c),
де a - бчна сторона, d- діагональ, с - більша основа.
p=(a+d+c)/2=52.
R=26520/(4*√52*39*12*1)=6630/√24336=6630/156=42,5 см.

ЗАДАЧА 5 Периметр рівнобедреного трикутника 64 см, а бічна сторона на 11 см більша від його основи. Знайдіть висоту трикутника, опущену на бічну сторону.
а) 13,66 см; б) 13,4 см; в. 13,44 см; г) 15,44 см.
Розв'язання: Складемо рівняння до умови.

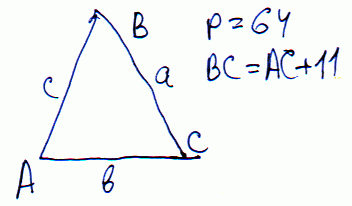
Позначимо основу через Х, тоді бічна сторона – Х+11.
Запишемо формулу периметру трикутника
P=2(X+11)+X=3*X+11.
З іншої сторони периметр рівний 64 см. Отримаємо рівняння
3*Х+22=64 (см.);
Х=(64-22)/3=14 (см.)
Бічна сторона рівна
X+11=25 см.
Знайдемо висоту
h=√ (25²-(14/2)²)=24 (см.)
Тоді площа рівнобедреного трикутника рівна
S=14*24/2=168 (см. кв.)
Таку ж площу отримаємо, якщо затимемо бічну сторону і висоту, проведену до неї
S=h1*25/2=168
Звідси знаходимо висоту
h1=168*2/25=13,44 (см).
Правильний варіант (в).

ЗАДАЧА 6 Висота рівнобедреного трикутника, проведена до основи, дорівнює 15 см, а висота, проведена до бічної сторони – 24 см. Знайдіть площу цього трикутника.
а) 270 см²; б) 300 см²; в) 310 см²; г) 285 см².
Розв'язання:Виконуємо схематично побудову до завдання.

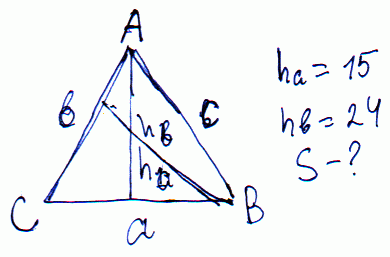
Складемо рівняння площі трикутника через відомі висоти.
S=a*24/2=b*15/2.
Звідси маємо відношення для вираження однієї сторони через іншу
b=24/15*a.
Далі за теоремою Піфагора виразимо висоту через бічну сторону і половину основи трикутника
h1=sqrt(a²-(b/2)²)=sqrt(a²-(24*a/15/2)²)=15 (см.).
Звівши під коренем до спільного знаменниа та виразивши невідому, отримаємо
a=15*30/18=25 (см.)
Далі знаходимо площу трикутника
S=24*25/2=300 (см. кв.)
Правильним є варіант (б).

ЗАДАЧА 7 Обчислить площу рівнобедреного трикутника, бічна сторона якого дорівнює 20 см, а висота, проведена до основи – 12 см.
а) 192 см²; б) 240 см²; в) 120 см²; г) 96 см².
Розв'язання:

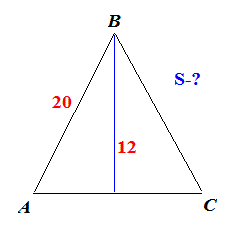
За Піфагором знаходимо основу рівнобедреного трикутника
AC/2=sqrt(20²-12²)=16 (см).
Знаходимо площу
S=1/2*AC*h=16*12=192 (см. кв.)
Варіант а) є правильним.

Задача 8 Бічна сторона рівнобедреного трикутника точкою дотику вписаного кола ділиться у відношенні 12 : 25, рахуючи від вершини кута при основі трикутника. Знайдіть радіус вписаного кола, якщо площа трикутника дорівнює 1680 см².

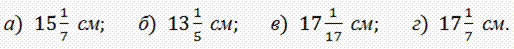
Розв'язання:

За умовою AD/DB=12/25, S=1680.
Позначимо AD=12x, DB=25x.
З геометрії слідує, що AM=12x, а основа трикутника рівна 24х.
З прямокутного прямокутника виразимо висоту
h²=x²((12+25)²-12²).
Далі складемо рівняння площі, але для зручності обчислень все помножимо на 2 і піднесемо до квадрату.
(24x)²*x²*((12+25)²-12²)=(2*1680².
Після обчислень отримаємо, що x=2 см.
Відповідно бічна сторона 37*2=74 см, а основа 24*2=48 см.
Радіус вписаного кола знайдемо розділивши площу трикутника на половину периметру.
P=74*2+48=196 см.
P/2=196/2=98 см.
r=1680/98=120/7=17 і 1/7.
З тестових відповідей правильний варіант (в).

Задача 9 На медіані ВD рівнобедреного трикутника АВС позначено точку М так, що ВМ : МD = 3 : 1. Знайдіть площу трикутника АВС, якщо площа трикутника АМD дорівнює 3см².
а) 27 см²; б) 24 см²; в) 30 см²; г) 25 см².
Розв'язання: Багато хто з Вас подумає, що завдання неможливо розвязати і потрібно застосовувати складні формули. Але по великому рахунку маємо приклад на логіку. Побудуємо схематично трикутник і зобразимо відому область.

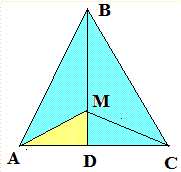
За простою формулою площа рівна пів добутку основи на висоту.
Якщо розглянути трикутники ABD і AMD то основа в них та сама, а висота відноситься як (3+1):1.
Таким чином площа трик. ABD в 4 рази більша ніж AMD, а цілого рівнобедреного трикутника в два рази більша ніж знайденого прямокутного ABD.
Площа S_[ABC]=2*4*S[AMD]=8*3=24 см. кв, що відповідає варіанту (б) тестів.
Ось такі прості міркування дозволяють розв'язати непросту на перший погляд головоломку.

Задача 10 Периметр рівнобедреного трикутника дорівнює 100 см, а висота, опущена на основу, – 30 см. Знайдіть площу трикутника.
а) 480 см²; б) 420 см²; в) 560 см²; г) 460 см².
Розв'язання: Маємо приклад на складання рівнянь.
Позначимо основу трикутника через a, а бічну сторону b.
Рівняння периметру дає залежність
P=2*b+a=100.
Запишемо формулу квадрату висоти трикутника
b²-(a/2)²=30².
З периметру виражаємо половину основи
a/2=(100-2b)/2=50-b
і підставяємо в друге рівняння
b²-(50-b)²=30².
Після спрощень отримаємо
100*b=50²+30²
звідси
b=34 см.
а=100- 2b=100-2*34=32 см.
Маємо основу і висоту, можемо визначити площу трикутника
S=1/2*a*h=32*30/2=480 (см. кв.)
Це відповідає варіанту (а) тестових відповідей.

Задача 11 У рівнобедреному трикутнику бічна сторона дорівнює 10см, а висота, що проведена до основи, – 6 см. Знайти площу трикутника.
а) 96 см2; б) 60 см2; в) 48 см2; г) 36 см2.
Розв'язання: Виконуємо допоміжний рисунок до завдання.

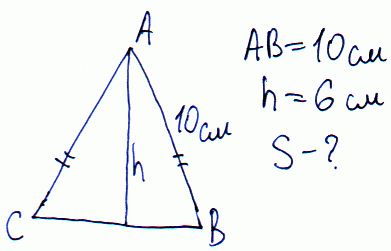
Завдання на застосування теореми Піфагора.
Обчислюємо половину основи трикутника
a/2=sqrt(10²-6²)=8 см. а=2*8=16 см.
Обчислюємо площу трикутника
S=16*6/2=48 (см. кв.)
Вірною відповіддю на тестах є варіант (в).

Задача 12 У рівнобедреному трикутнику висота, проведена до бічної сторони, поділяє її на відрізки 8 см і 2 см, починаючи від вершини кута між бічними сторонами. Знайдіть площу трикутника.
Розв'язання:

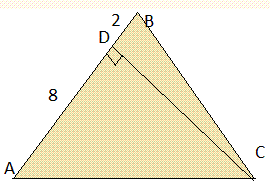
З рисунку можемо бачити сам хід обчислень. Спершу знайцдемо висоту, а далі площу.
Гіпотенуза трикутника DBC рівна
2+8=10 см.
Обчислюємо висоту
10²-2²=h²;
h^2=96;
h=4*sqrt(6).
Далі знаходимо площу
S=1/2*10*4√6=20√6 см.

Задача 13 Периметр рівнобедреного трикутника дорівнює 128 см, а бічна сторона відноситься до основи, як 5:6. Обчислити діаметр вписаного кола.
Розв'язання: Позначимо основу через 6*a, бічну відповідно – 5*a.

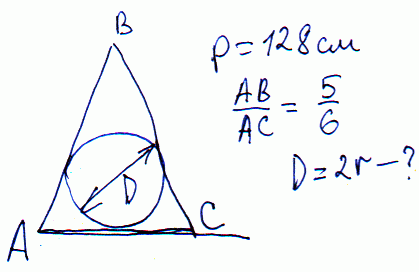
Складаємо рівняння периметра
P=2*5*a+6*a=16*a.
Звідси a=128/16=8 см.
Відповідно до параметра основа рівна 6*a=48 см,
сторони трикутника 5*8=40 см.
Знайдемо висоту за відомою формулою
h=sqrt(40²-24²)=32 см.
Обчислюємо площу S=48*32/2=768 см. кв.
Радіус вписаного у трикутник кола рівний частці площі до половини периметра
R=768/(128/2)=12 см.

Задача 14 Периметр рівнобедреного трикутника дорівнює 160 см, а висота, опущена на основу дорівнює 40см. Знайти всі сторони трикутника.
Розв'язання:

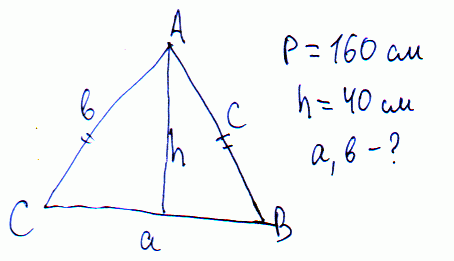
Складаємо два рівняння: висота через теорему Піфагора і периметр.
a+2*b=160;
b²-(a/2)²=40².
З першого виражаємо a/2 і підставляємо в друге
b^2-(80-b)^2=40^2.
Звідси
160*b=40²+80²;
b=50 см.
a=160-2*50=60 см.
Сторони триутника рівні 50, 50, 60 см.

Задача 15 Бічна сторона рівнобедреного трикутника дорівнює 55 см, а його основа дорівнює 66см. Обчислити довжину відрізків, на які ділить бічну сторону бісектриса кута при основі.
Розв'язання: Позначимо через x, y – відрізки, на які ділить бісектриса бічну сторону.

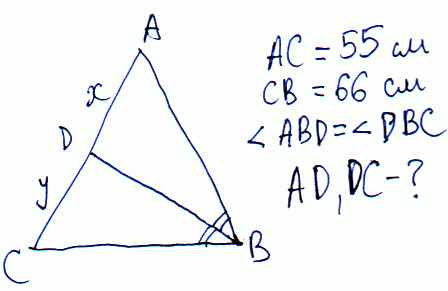
За теоремою про пропорційні відрізки маємо
55/x=66/y, x=55/66*y.
Друге співвідношення дає умова, що сума відрізків рівна бічній стороні
x+y=55.
При підстановці першого в друге отримаємо
(55/66+1)*y=55.
Звідcи y=30 см, x=55-30=25 см.
На цьому всі обчислення до цього завдання.

Задача 16 Бічна сторона і основа рівнобедреного трикутника відносяться, як 5:6, а периметр його дорівнює 48 см. Знайти відстань від точки перетину медіан до основи.
Розв'язання: Позначимо сторони трикутника через 5x, 6x відповідно.

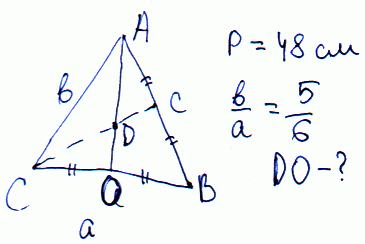
Тоді рівняння периметру запишемо у вигляді
2*5*x+6*x=48;
16*x=48;
х=48/16=3 см.
Звідси обчислюємо – основу
6*x=18 см
та бічні сторони – 5*x=15 см.

Задача 17 Бісектриса проведена до бічної сторони рівнобедреного трикутника, ділить її на відрізки 25 см і 30 см , починаючи від вершини, яка протилежна основі. Обчислити периметр трикутника.
Розв'язання: Позначимо основу і бічну сторони через a, b відповідно.

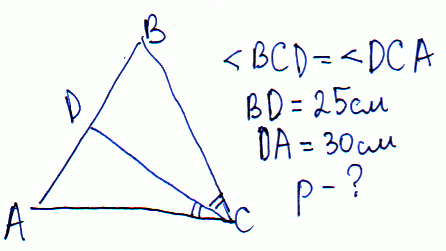
За властивістю складаємо відношення a/30=b/25.
З іншої сторони бічну сторону можемо визначити
b=25+30=55 см.
Виразимо основу з першої залежності
a=30*b/25=30*55/25=66 см.
Знаходимо периметр
P=66+2*55=176 см.

Задача 18 Бічна сторона рівнобедреного трикутника дорівнює 25 см, а висота, опущена на неї - 24 см. Знайти периметр трикутника.
Розв'язання: Теж не простий на перший погляд приклад. Виконуємо побудову до рисунку.

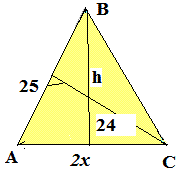
Площа рівна півдобутку основи на висоту. З однієї сторони це
S=1/2*25*24=300 см. кв.
З іншої сторони позначимо основу через 2x, за теоремою Піфагора знайдемо висоту, а далі й площу
h=sqrt(25²-x²); S=1/2*2*x* sqrt(25²-x²).
Прирівнявши площі, отримаємо рівняння для відшукання основи
x*sqrt(25²-x²)=300.
Піднесемо до квадрату та згрупуємо, в результаті отримаємо біквадратне рівняння
x⁴-225*x²+90000=0.
Виконавши заміну y=x², зведемо його до вигляду
y²-225*y+90000=0.
Корені квадратного рівняння рівні
y1=400, y2=225.
Звідси x1=20, x2=15.
Основа рівна 2*x, тому в першому випадку вона рівна 40 см, в другому 30 см. Багатьом з Вас незрозуміло, як таке може бути. Справа в тому, що при основі 40 висота буде проектуватися не на бічну сторону, а на її продовження. Тому такий варіант хоч і правильний геометрично, проте ми його виключаємо. Остаточно периметр рівний
P=2*25+30=80 см.

Задача 19 У рівнобедреному трикутнику висота , опущена на основу, дорівнює 32 см. Бісектриса кута при основі перетинає дану висоту в точці , яка віддалена від основи на 12 см. Знайти основу трикутника.
Розв'язання: Дещо підправимо попередній рисунок до нового завдання. В «Paint» це робити доволі легко.

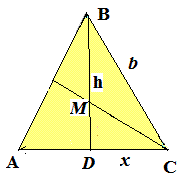
Оскільки MD=12, а висота h=32 то BM=32-12=20 см.
За властивістю бісектриси вона ділить висоту на пропорційні сторонам відрізки, тобто
b/20=x/12.
Друге рівняння отримаємо з теореми Піфагора
b²-x²=h²=32².
Виражаємо з першої залежності одну з невідомих та підставляємо у друге
x=12/20*b;
b²-(12/20*b)²= 32².
Розв'язок рівняння b=40 см.
Знаходимо другу невідому - x=12/20*40=24 см.
Так, як осова трикутника в два рази більша за x, то вона рівна 48 см.
Постарайтеся завчити або згрупувати в пам'яті подібні схемки обчислень, на контрольній та тестах це допомогає у виборі правильного (швидкого) методу розрахунків.

Задача 20 У рівнобедреному трикутнику кут, утворений висотою, проведеної до основи, і бісектрисою кута при основі, дорівнює 55 град. Знайти всі кути трикутника.
Розв'язання: Виконаємо допоміжний рисунок.

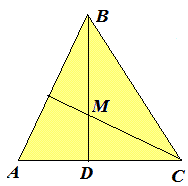
Кут DMC рівний 55 градусів. Кут DCM рівний 180-90-55=35 градусів.
Оскільки маємо бісектрису, то кут MCB=DCM=35.
Кут при основі має 2*35=70 градусів.
При вершині рівнобедреного трикутника кут рівний
180-2*70=40 градусів.
На цьому всі кутові міри знайдено.

Задача 21 У рівнобедреному трикутнику основа дорівнює 10 см, а висота – 20 см. Знайти висоту опущену на бічну сторону.
Розв'язання:

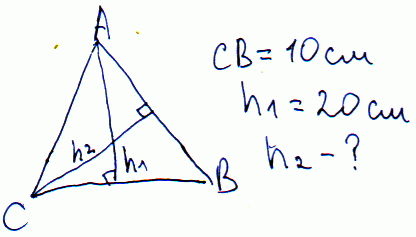
Знайдемо невідому висоту через рівняння площі
S=1/2*20*10=100 см. кв.
Обчислимо бічну сторону
b=sqrt(20²-(10/2)²)=5√15
і площу
S=1/2*b*h=100;
h₂=2*100/b=8/3*√15 см.

Задача 22 Основа рівнобедреного трикутника дорівнює 30 см, а висота опущена на бічну сторону – 24 см. Обчислити периметр трикутника.
Розв'язання: Позначимо відрізки на які ділить бічну сторону висота через a,b, починаючи з основи.

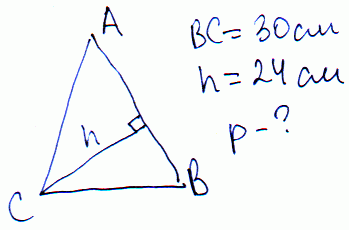
За теоремою Піфагора складаємо 2 рівняння:
a²=30²-24²;
(a+x)²-x²=24².
При обчисленні системи рівнянь отримаємо значення
x=7,a=18.
Звідси бічна сторона рівнобедреного трикутника рівна 18+7=25 см, а його периметр
P=30+2*25=80 см.

Задача 23 На медіані рівнобедреного трикутника, проведеної до основи, взято точку , що однаково віддалена від кінців бічної сторони. Обчислити периметр трикутника якщо відстань від цієї точки до основи дорівнює 14 см, а до кінця основи – 50 см.
Розв'язання: Без додаткової побудови тут не розібратися.

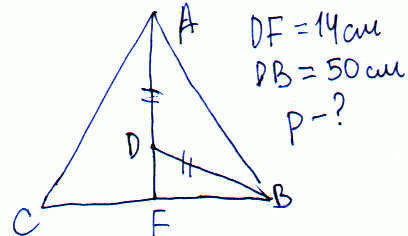
З малюнку бачимо, що половину основи можемо знайти з прямокутного трикутника
a²=50²-14²
звідси a=48 см, а основа рівна 2*48=96 см.
Також за умовою, частина висоти після точки рівна 50 см, а вся висота 50+14=64 см.
З прямокутного трикутника виражаємо бічну сторону
c^2=64^2-48
звідси c=80 см.
Знаходимо периметр
P=80*2+96=256 см.
Всюди де Вам незрозуміла умова, чи що від Вас вимагають -використовуйте допоміжні малюнки. В більшості задач це дозволяє побачити хід подальших обчислень.

Задача 24 Медіана рівнобедренного трикутника , проведена до основи, ділить висоту, опущену на бічну сторону, на відрізки 75 і 21см. починаючи від кінця основи. Знайдіть сторони трикутника.
Розв'язання: Спершу виконуємо допоміжну побудову.

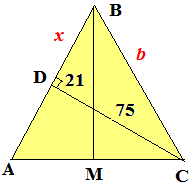
За вастивістю рівнобедреного трикутника медіана проведена до основи одночасно є і висотою і бісектрисою. Тому з однієї сторони можемо скласти залежність
x/21=b/75.
З іншого боку, трикутник CDB прямокутний, тому за теоремою Піфагора маємо
x^2+(21+75)^2=b^2.
Виразимо з першого рівняння x та підставимо у друге
x=21/75*b;
96²=b²-(21/75*b)².
В результаті обчислень отримаємо b=100.
Тоді одна з частинок , що відтинає висота від бічної сторони рівна
X=21*100/75=28 см.
Решта AD рівна
AD=100-28=72 см.
Основу рівнобедреного трикутника знаходимо як гіпотенузу
ADC 72²+96²=a².
Звідси a=120 см.
Сторони рівні 120 см та дві по 72 см.