Рівнобедрений трикутник – це трикутник у якого дві сторони або 2 внутрішні кути рівні між собою. Інша властивість полягає в тому, що висота проведена до основи рівнобедреного трикутника одночасно є і бісектрисою кута при вершині і медіаною трикутника. Доволі прості властивості, які виділяють рівнобедрені трикутники серед інших (прямокутних, рівносторонніх).
Для засвоєння та повторення матеріалу за 5-6 клас теми "трикутники" нагадаємо їх класифікацію.
Залежно від міри кутів трикутники поділяються на :
- гострокутні;
- прямокутні;
- тупокутні.

Залежно від довжини сторін трикутники поділяють на
- рівносторонні;
- рівнобедрені;
- різносторонні.
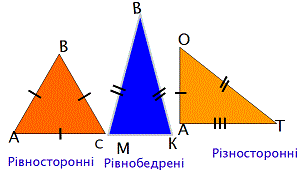
Основні ознаки рівнобедреного трикутника
1. Якщо маємо трикутник в якому два кути рівні, то він рівнобедрений.
2. Трикутник рівнобедрений, якщо:
- одна з його висот є медіаною;
- одна з його медіан є бісектрисою;
- одна з його висот є бісектрисою.
3. Трикутник рівнобедрений, якщо:
- дві його висоти рівні;
- дві його медіани рівні;
- дві його бісектриси рівні.
Починають вивчати трикутники у 5-7 класі в курсі геометрії шкільної програми із простих завдань на засвоєння означення рівнобедреного трикутника, а також на сторони і кути трикутника. Для прикладу, "Визначити кути при основі, якщо кут при вершині рівний 110 градусів". 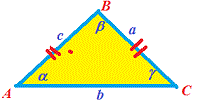
Обчислення таких завдань простіше простого. Сума кутів трикутника рівна 180 градусів, кути при основі (beta) рівні. Звідси на всі випадки кутів при вершині alpha слід застосовувати формулу
beta=(180-alpha)/2.
Якщо кут при вершині 110 градусів то біля основи рівнобедреного трикутника кути рівні
beta=(180-110)/2=35 (градусів).
Нехай задано кут при основі рівнобедреного трикутника і він рівний 50 градусів, тоді кут при вершині рівний
alpha=180-2*50=80 (градусів).
Міняєте в формулі значення кута (50) на свій і знаходите кут у вершині трикутника для будь-якого рівнобедреного трикутника.
В міру вивчення властивостей трикутника, формул для вписаних та описаних кіл, зростає і складність обчислень і різноманітність задач, які можна розв'язати. Таким чином в 8-9 класі задачі на трикутники вимагають знань чимало важливих формул без яких обчислення неможливо виконати.
Найпоширеніші та найпростіші формули – це периметр та площа рівнобедреного трикутника. Тут ніякі властивості трикутника не спрощують вказаних величин і їх знаходимо за загальними формулами трикутника
p=a+b+c;
S=1/2*a*h – площа трикутника рівна півдобутку сторони на висоту проведену до цієї сторони. Друга поширена формула застосовується, якщо відомі сторони та кут між ними.
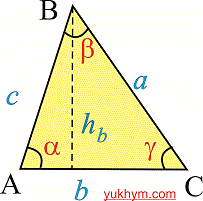
Тоді площа трикутника рівна півдобутку сторін на кут між ними. Згідно наведеного рисунку маємо
S=1/2*a*b*sin(hamma);
S=1/2*b*c*sin(alpha);
S=1/2*a*c*sin(beta).
Якщо задана одна із рівних сторін і кут при вершині то площа рівна
a=b S=1/2*a*a*sin(hamma).
Приклади на рівнобедрений трикутник
Частину прикладів, що наведені можна назвати усними, оскільки міркування для пояснення обчислень чи доведень можна виконати в голові без застосування ручки і зошита.
Приклад 1. Чи є рівнобедреним будь-який рівносторонній трикутник?
Чи є рівностороннім будь-який рівнобедрений трикутник?
Відповідь: будь-який рівносторонній трикутник зажди буде рівнобедреним. А от обернене твердження не вірне. Не всі рівнобедрені трикутники є рівносторонніми, а лише такі в яких всі сторони або кути рівні.
Приклад 2. У трикутнику ABC сторони AB=BC рівні. Назвіть рівні кути трикутника.
Відповідь: Спільною для сторін є вершина В, отже кути при інших основах рівні між собою < A=< C.
Приклад 3. Кут між висотою і стороною рівнобедреного трикутника рівний 30 градусів. Знайти кут при основі.
Розв'язання: Оскільки в рівнобедреному трикутнику висота є одночасно бісектрисою, то повний кут при вершині рівний подвійному заданому
beta=2*30=60 (градусів).
Обчислюємо кут при основі трикутника
alpha=(180-60)/2=60 (градусів).
Оскільки всі кути при вершинах трикутника рівні, то заданий трикутник є рівностороннім.
Приклад 4. Які кути при основі повинен мати трикутник, щоб він був одночасно і рівнобедреним і прямокутним?
Розв'язання: Прямокутний трикутник має прямий кут (90 градусів) – це знають усі. Знайдемо кути при основі за формулою
alpha=(180-90)/2=45 (градусів).
Таким чином рівнобедрений прямокутний трикутник повинен мати кути 45, 45, 90 градусів.
Приклад 5. Висота рівнобедреного трикутника рівна половині основи. Знайти кут при основі трикутника.
Розв'язання: Оскільки висота перпендикулярна до основи і рівна її половині, то кут між основою і висотою та висотою і стороною рівні між собою і складають 45 градусів. Якщо Вам це важко усвідомити то привчіть себе виконувати побудову до умови завдання. Багатьом це допомагає швидше засвоїти матеріал.
Приклад 6. Периметр рівнобедреного трикутника дорівнює 2,6 м. Знайдіть сторони трикутника, якщо його основа більша від бічної сторони на 0,5 м.
Розв'язання: В такого типу задачах потрібно скласти рівняння. Позначимо сторону трикутника через t. Тоді основа за умовою рівна
t+0,5м.
Складаємо рівняння
t+t+t+0,5=2,6;
3*t=2,6-0,5=2,1;
t=2,1/3=0,7 (м).
Приклад 7. Периметр рівнобедреного трикутника дорівнює 20см.
Знайдіть:
а) основу трикутника, якщо його бічна сторона дорівнює 7,5 см;
б) бічну сторону трикутника, якщо його основа дорівнює 4 см;
в) сторони трикутника, якщо його бічна сторона відноситься до основи як 3 : 4.
Розв'язання: a) Для обчислення основи від периметра віднімемо рівні сторони
b=20-2*7,5=6 (cм).
б) Знайдемо бічну сторону рівнобедреного трикутника за формулою
a=(20-4)/2=8 (cм).
в) Згідно пропорції між стороною і основою рівнобедреного трикутника введемо позначення
сторона рівна – 3*Х;
Тоді основа – 4*Х.
Складаємо рівняння периметра
3*Х+3*Х+4*Х=20;
10*X=20;
X=20/10=2 (cм).
Обчислюємо сторони трикутника
3*2=6 (см);
4*2=8 (см).
Отже сторони трикутника рівні 6, 6, 8 см.
Приклад 8. Периметр рівнобедреного трикутника ABC дорівнює 18 см, причому основа AC менша за бічну сторону на 3 см. Знайдіть основу трикутника ABC.
Розв'язання: Вводимо позначення: основа – Х, сторона – Х+3.
Складаємо рівняння
Х+2*(Х+3)=18;
3*Х=18-6=12;
Х=12.3=4 (cм).
Відповідь: основа трикутника рівна 4 см.
Задачі на площу трикутника
Задача 1. Сторони рівнобедреного трикутника 5 см, основа – 6 см. Знайдіть площу трикутника .
Розв'язання: Спершу виконуємо побудову до завдання. 
Для обчислення площі нам крім основи потрібно знайти висоту трикутника. Відомо, що висота є медіаною рівнобедреного трикутника, тобто ділить основу на два відрізки по 6/2=3 (см). Далі обчислюємо висоту як катет прямокутного трикутника
h2=52-32=25-9=16;
h=sqrt(16)=4 (см).
Обчислюємо площу трикутника
S=1/2*6*4=12 (сантиметрів квадратних).
Відповідь: 12.
Задача 2. Сторони рівнобедреного трикутника 10 см, а висота опущена до основи – 8 см. Знайдіть площу трикутника .
Розв'язання: Побудуємо трикутник. Половину сторони основи позначимо через x. За теоремою Піфагора складемо рівняння
82+x2=102;
x2=100-64=36;
x=6 (см).
Повна основа в два рази більша – 12 см. Знаходимо площу трикутника
S=12*8/2= 48 (сантиметрів квадратних).
Задача 3. Сторони рівнобедреного трикутника рівні 5, 5, 6 см. Знайти радіус кола описаного навколо трикутника.
Розв'язання: Для обчислення радіуса описаного навколо трикутника кола необхідно знати формулу
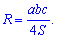
Оскільки сторони відомі то площу можемо знайти через формулу Герона, однак це складний шлях. Простіше за теоремою Піфагора знайти висоту трикутника. Оскільки висота є перпендикуляром до основи і , одночасно медіаною, то висота рівна катету прямокутного трикутника з гіпотенузою 5 см та катетом
6/2=3 см.
Обчислюємо висоту
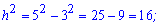
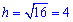 (см).
(см).
Знаходимо площу трикутника
S=1/2*6*4=12 (сантиметрів квадратних).
Далі маємо всі дані для обчислення радіуса опиcаного навколо трикутника кола
R=5*5*6/12=12,5 (см).
Відповідь: радіус описаного кола 12,5 см.
В інтернеті чимало прикладів на рівнобедрений трикутник. Частина з них подібні на розглянуті завдання, інші - складніші і вимагають застосування більшої кількості формул. Властивості рівнобедреного трикутника часто зустрічаються в задачах на ромб, піраміду, трапеції. Тому, вивчивши базові формули та правила на простих фігурах, на складніших застосовувати знання стає набагато простіше.


