Завдання на часткові похідні розв'язують студенти на 1, 2 курсі навчання. Такі приклади задають і заочникам, і студентам стаціонарної форми.
Перші завдання досить прості, однак на контрольній та тестах задають складні приклади на обчислення часткових похідних. Все залежить від складності функції багатьох змінних – поліноми та прості тригонометричні функції піддаються диференціюванню без значних труднощів, а от дробово-раціональні функції, комбінації раціональних та показникових вимагають більшої уваги та часу для знаходження похідних.
Схема обчислень похідної від функції двох змінних достатньо проста – змінну по якій не диференціюють вважають константою при обчисленні і першої, і другої похідної. На практиці це виглядає наступним чином.
Приклад 1. Знайти часткові похідні й повний диференціал першого порядку функції
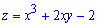в точці N(1;2) при заданому аргументі x:
delta[x]=0,03; delta[y]=-0,02
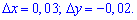
Розв'язання: Знайдемо часткові похідні першого порядку від заданої функції двох змінних:
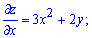
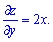
В точці N(1;2) вони рівні
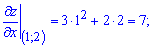
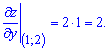
Повний диференціал знайдемо за формою
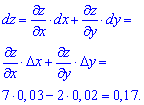
Із обчислень бачимо, що знайти повний диференціал функції під силу кожному.
Приклад 2. Знайти часткові похідні другого порядку функції
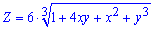Розв'язання: Обчислюємо часткові похідні першого порядку від заданої функції двох змінних:
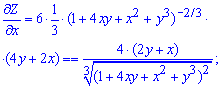
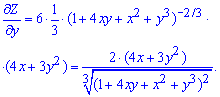
Далі повторним диференціюванням по кожній із двох змінних знаходимо часткові похідні другого порядку.
Друга похідна по "ікс" прийме значення
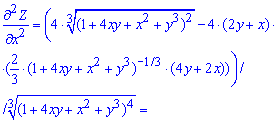
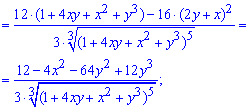
Друга похідна по "ігрику"
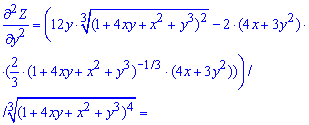
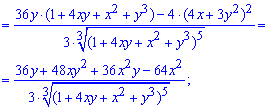
Друга похідна по "ікс ігрик" (мішана похідна)
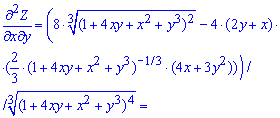
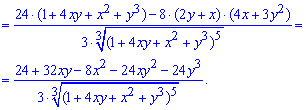
При диференціюванні використовували правило похідної частки функцій.
Приклад 2*. Довести, що функція z=f(x,y) задовольняє наведеному рівнянню:
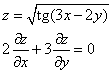
Обчислення: Знайдемо часткові похідні функції І порядку:
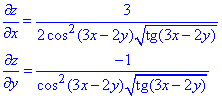
Підставимо отримані вирази у рівняння:
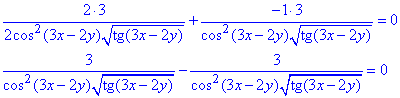
Тотожністьз умови виконується 0+0= 0, отже задана функція задовольняє наведеному рівнянню, що і треба було довести.
Приклад 3. Обчислити часткові похідні другого порядку функції
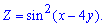Розв'язання: Знаходимо часткові похідні першого порядку від квадрату синус функції від двох змінних:
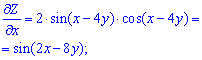
Тут спростили вираз за формулою синуса подвійного кута.
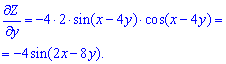
Повторним застосуванням похідної знаходимо часткові похідні II порядку
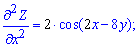
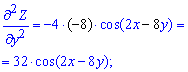
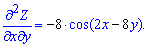
Це і є відповіддю до задачі.
Приклад 4. Дослідити на екстремум функцію двох змінних
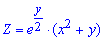Розв'язання: Запам'ятайте алгоритм знаходження точок екстремуму:
Для цього обчислюємо часткові похідні першого порядку
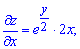
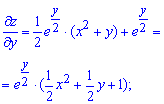
та прирівнюємо їх до нуля.
В результаті отримаємо систему двох рівнянь, яку і розв'язуємо
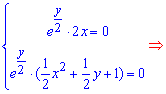
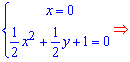
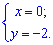
Критична точка рівна (0;-2).
Щоб встановити характер екстремуму, тобто чи в критичній точці досягаємо максимуму або мінімуму слід знайти похідні другого порядку в точці
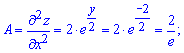
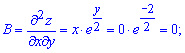
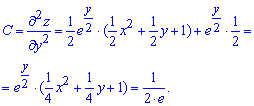
і визначити знак диференціалу
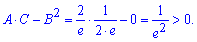
Оскільки A>0 та параметр D=A*C-B*B>0 більший нуля, то функція має мінімум в знайденій точці.
Знайдемо значення функції в точці
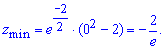
Графік функції двох змінних в околі точки мінімуму має вигляд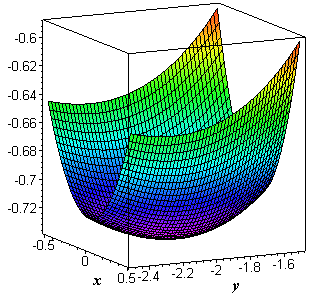 
Такого роду приклади на часткові похідні зустрічаються на перших двох курсах навчання математичних дисциплін. Якщо Вам не під силу знайти часткові похідні функції першого та другого порядку, в навчанні зустрічаються складні функції, або навчаєтеся заочно тоді звертайтеся до нас.
Через форму зворотнього зв'язку Ви завжди можете замовити розрахункову роботу, контрольну чи консультацію.
Пам'ятайте, що сайт постійно оновлюється і наповнюється новими уроками, одна з цілей яких – допомогти Вам у навчанні!
