Текстовых задачи на составление уравнений взяты из сборника "Тестовые задания для поступающих. Математика" (стр. 84) изданного в 2001 году Волынским государственным университетом имени Леси Украинки. Приведенные задачи соответствуют уровню повышенной сложности и научат Вас строить уравнения и находить неизвестные величины. Кроме того Вы познакомитесь с простыми и эффективными методиками решении уравнений и системы уравнений. Ответы к задачам для школьников 9, 10 классов возможно и тяжелые, а всем кто готовится к олимпиаде или вступлению в ВУЗ станут хорошим репетитором и помощником.
Задача 1. Сравнивая два бруска, имеющие форму прямоугольного параллелепипеда выяснили, что длина, ширина и высота второго бруска соответственно на 2 см больше чем первого, а объем и полная поверхность второго бруска соответственно на 138 см3 и 120 см2 больше чем первого. Какая полная поверхность второго бруска (у см2 )?
Решение: Заданное задание имеет непростой алгоритм вычислений. При одинаковых обозначениях сторон запишем уравнения, которые следует решать
(a+2)*(b+2)*(c+2)=a*b*c+138;
2*(a+2)(b+2)+ 2*(b+2)*(c+2)+2*(a+2)*(c+2)=S+120.
Нужно найти площадь S. После раскрытия скобок и упрощений получим
S+4*(a+b+c)+8=138;
8*(a+b+c)+12=120.
Выразим из второго уравнения нужные слагаемые и подставим в первое
4*(a+b+c)=120/2-12/2=60-6=54;
S=138-8-54=76 (см. квадратных).
Ответ: S=76.
Задача 2. Искомое трехзначное число начинается с цифры 1. Если ее вытереть и потом дописать вместо последней цифры числа, то образованное новое трехзначное число будет больше искомое на  . Найдите искомое число.
. Найдите искомое число.
Решение: По свойствам логарифма упростим число
Уравнение к задаче будет выглядеть следующим образом
ab1-1ab=90.
Начнем решать его из единиц
1-b=0; b=1.
Начальное условие упростится к виду
a11-1a1=90.
Без вычислений можно догадаться, что вторая цифра равна a=2.
Итак загаданное число равно 121.
Ответ: 121.
Задача 3. По двум сторонам прямого угла в направлении к его вершине движутся два тела. В начальный момент тело А находится от вершины прямого угла на расстоянии 60 м, а тeло В - на расстоянии 80 м. Через 3 с расстояние между А и В стало равным 70 м, а еще через 2 с – 50 м. Найти скорость тела А (в м/с).
Решение: Уравнения движения тел можно записать формулой
60-V[a]*t;
80-V[b]*t.
Поскольку они движутся по сторонам прямого угла то расстояние между ними находим по теореме Пифагора. В результате получим два уравнения для нахождения неизвестных скоростей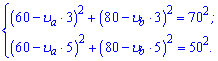
Нужно выразить с произвольного с уравнений скорость тела В и подставить в другое. В результате получим иррациональное уравнение относительно V [a].
Вы делайте нужные преобразования самостоятельно, а я научу Вас, как это сделать в математическом пакете Maple.
В Мэйпл решение системы уравнений можно найти одной строкой кода, а для решения уравнений используют команду solve.
> restart;
> solve({(60-V[a]*3)^2+(80-V[b]*3)^2=70^2,(60-V[a]*5)^2+(80-V[b]*5)^2=50^2},{V[a],V[b]})
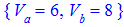
Из ответа видно что искомая скорость равна 6 метров в секунду.
Ответ: 6 м/с.
Задача 4. Свежие огурцы содержат 98% воды и весят 100 кг. Когда огурцы подсохли то воды в них стало 96%. Сколько стали весить огурцы после подсыхания (в килограммах)?
Решение: Вычислим сколько сухой массы в огурцах
100*(100-98)/100=2 (кг).
Подсохшие огурцы имеют 96 % воды и (100-96)=4 % воды..
Составим пропорцию
2 – 4 %
X – 100%
Из пропорции найдем полную массу подсохших огурцов
X=100*2/4=50 (кг).
Подобным образом ищут ответы и в задачах о грибах, яблоках, грушах, сливах, поэтому запомните простую схему вычислений.
Ответ: 50 кг.
Задача 5. Пчелы, перерабатывая цветочный нектар в мед освобождают его от большого количества воды. Сколько килограммов нектара приходится переделывать пчелам для получения 1 кг меда, когда известно, что нектар содержит 75% воды, а полученный из него мед -17% воды?
Решение: Итак известно, что нектар содержит 75 % воды, мед– 17%.
Найдем количество 100 % меда
1 кг – 100%
X – (100-17)%.
X=83/100=0, 83 (кг).
Вычислим количество (100-75)=25 % сухой массы нектара. Составляем вторую пропорцию для вычисления массы всего нектара
0,83 – 25%
Y – 100%.
Выполним вычисления
Y=0,83*100/25=3,32 (кг).
Так что для получения 1 кг меда пчелы должны переделать 3,32 кг нектара.
Как видите вычисления не сложные, главное - понять принцип записи пропорций.
Задача 6. Три тракторные бригады вместе вспахивают поле за 4 дня. Это же поле первая и вторая бригады вместе могут вспахать за 6 дней, а первая и третья вместе - за 8 дней. Во сколько раз площадь, которую вспахивает за день вторая бригада больше площади, которую вспахивает за день третья бригада?
Решение: Задачи на совместную работу даются многим трудно, поскольку не все понимают, как составить уравнение?
Однако нужно пользоваться общими формулами: "производительность" умножить на "время" = "работа".
Составляем соответствующие уравнения
(a+b+c)*4=A;
(a+b)*6=A;
(a+c)*8=A.
С записи можно догадаться, что a, b, c - производительность 1, 2, 3 бригад; A - условное обозначение площади поля.
Запишем полученную систему уравнений так чтобы производительность в левой стороне уравнений была без времени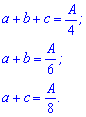
Для отыскания производительности бригад, о которых спрашивают, от 1 уравнения вычтем 2 и (1-3). В результате получим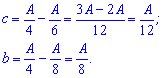
Во сколько раз больше площадь означает, что нужно b/c. 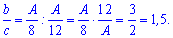
Получили ответ: в 1,5 раза вторая бригада вспахивает болше поля чем третья.
Задача 7. Две точки, двигаясь по кругу в одном направлении встречаются через каждые 56 минут; двигаясь в противоположных направлениях - через каждые 8 мин. Найти скорость первой точки (в м/мин), когда известно что за 1 секунду первая точка проходит на 1/12 метр больше чем вторая.
Решение: Сначала переведем путь пройденный за 1 секунду в скорость – 1/12 м/с.
В нужной системе единиц эта скорость составит 1/12*60=5 метров в минуту.
Введем обозначения, пусть первая точка движется со скоростью V, тогда скорость второй - V-5. Такое обозначение удобное для вычислений, так как при решении уравнений сразу находим нужную скорость.
Двигаясь по кругу быстрее первая из точек проходит полный круг S и часть второго круга до встречи со второй точкой. В уравнениях это будет отображаться записью
V*56=S+(V-5)*56;
V*56-(V-5)*56=S.
Двигаясь в противоположных направлениях они встречаются каждые 8 минут. Это означает что в сумме каждые 8 минут они проходят круг S, т.е.
V*8+(V-5)*8=S.
Вычтем из первого уравнения 2, чтобы избавиться длины окружности S.
V*(56-8)-(V-5)*(56+8)=0;
V*48-V*64+64*5=0;
16*V=64*5;
V=64/16*5=4*5=20 (м/мин).
Хорошо разберите схему решения задачи на движение по кругу, для многих из Вас подобное задание дается трудно.
Ответ: 20 м/мин.
Задача 8. Две точки, двигаясь по кругу в одном направлении встречаются через каждые 56 минут; двигаясь в противоположных направлениях - через каждые 8 мин. Найти длину окружности (в метрах) когда известно, что за 1 секунду первая точка проходит на 1/12 метра больше чем вторая.
Решение: До вычисления уравнений схема анализа задачи один к одному повторяет предыдущее задание.
Далее с одного уравнения нужно выразить скорость через путь и подставить во второе уравнение. Поскольку скорость нам известна, то подставим ее во второе уравнение предыдущего задания
S=16*V-40=16*20-40=280 (метров).
Ответ: длина окружности 280 метров.
Посмотреть похожие материалы:


