Проаналізуємо відповіді з робіт, які будуть корисними для Вас в курсі вищої математики. Цього разу розберемо 14 нових завдань, які містять особливості, розкриття яких можливе при знанні методів розкриття ірраціональностей, скорчення дробу на домінантний множник, першої та другої чудових границь та їх наслідків, розкладу функцій в ряд Тейлора та ще кілька прийомів. Перелічення в одному реченні великої кількості способів позбутися невизначеності границі на одних студентів наганяє страх і паніку, проте наступні відповіді доведуть, що на практиці все набагато простіше, якщо знати ряд правил.
Приклад 21 Обчислити границю послідовності:
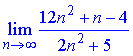
Розв'язання: Для знаходження границі частки поліномів виносимо n^2 з чисельника і знаменника дробу та спрощуємо на них.
В результаті залишаться сталі та нескінченно малі величини. Ліміт послідовності рівний частці сталих (=6).
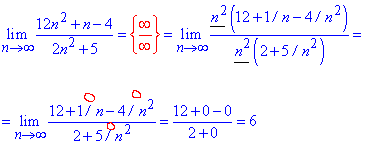
Спробуйте самостыйно цей же приклад обчислити за правилом Лопіталя.
Приклад 22 Визначити границю послідовності
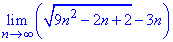
Розв'язання: Границю послідовності обчислюємо методом домноження на спряжений вираз. Таким чином отримаємо різницю квадратів і позбуваємося коренів в чисельнику.
Далі з чисельника та знаменника дробу виносимо n та спрощуємо на нього. Після цього оцінюємо дріб при граничному переході.
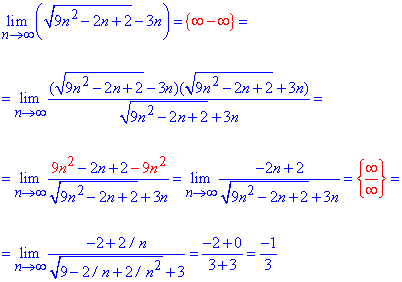
Приклад 23 Знайти границю функції
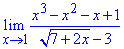
Розв'язання: Ліміт функції в точці дає невизначеність типу {0/0}. В чисельнику поліном розкладаємо на прості множники, в знаменнику позбуваємося ірраціональності множенням на спряжений вираз. Таким чином позбуваємося особливості в знаменнику, проте вона залишається в чисельнику. В результаті границя функції в точці рівна нулю.
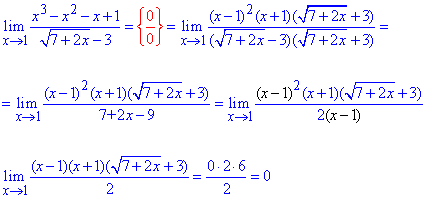
Приклад 24 Звести під важливі границі та обчислити
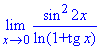
Розв'язання: Границя синуса до логарифма дає особливість {0/0}. Для її розкриття слід наведену функцію звести під першу та другу важливі границі та їх наслідки.
Для цього домножуємо та ділимо на вирази, яких не вистачає до чудових границь. Далі групуємо та зводимо до добутку границь, частина з яких рівна 1.
Все що залишиться і становить границю функції.
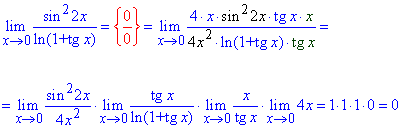
Приклад 25 Чому дорівнює ліміт функції?
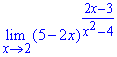
Розв'язання: Наведена границя має особливість – одиницю в степені безмежність. Розкриваємо її методом виділення другої чудової границі, яка рівна експоненті.
Для цього виділяємо всюди вирази (x-2), що вносять особливість, а далі переходимо до нової змінної t=x-2.
В показнику виділяємо обернений множник (-1/2t) до доданка при одиниці в дужках (1-2t).
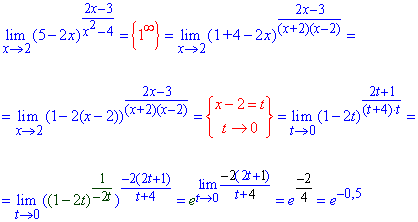
Таким чином отримаємо експоненту в степенті - ліміт функції, що залишилася.
Приклад 26 Обчислити границю послідовності
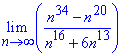
Розв'язання: Якщо змінна прямує до безмежності 
, то найбільший вклад вносить змінна в найстаршому степені. Виділимо їх в чисельнику та знаменнику
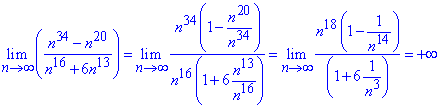
Далі, якщо в чисельнику старший степінь, то границя прямує до безмежності.
Приклад 27 Знайти границю
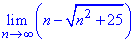
Розв'язання: Якщо підставити безмежність в послідовність отримаємо невизначеність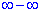 
. Щоб розкрити невизначеність, поділимо та помножимо на вираз, щоб в чисельнику отримати різницю квадратів
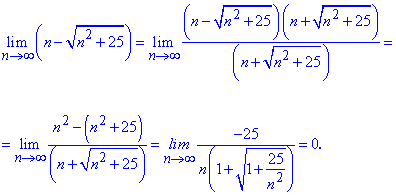
Границя рівна нулю, оскільки степінь знаменника вищий степеня чисельника (1>0).
Приклад 28 Обчислити границю послідовності
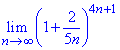
Розв'язання: Дану границю слід звести під правило другої важливої границі. Для цього в показнику утворюємо число, яке є обернено пропорційне до доданку біля одинички в дужках.
Сталий множник при цьому і буде показником експоненти в границі
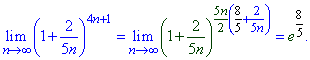
Приклад 29 Знайти границюі послідовності
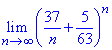
Розв'язання: Оскільки обидва значення в дужках менші одиниці (особливо важлива стала 5/63<1), а одне з них, що залежить від номера прямує до нуля, то їх сума в степені (n) також прямує до нуля
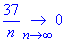
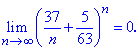
Приклад 30. Відомо, що ліміт послідовності рівний 13
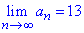
Знайти наступну границю
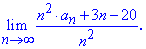
Розв'язання: Виділимо в чисельнику та знаменнику доданок, який вносить найбільший вклад в границю та розділимо на нього
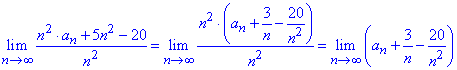
Доданки 3/n, -20/n^2 прямують до нуля при номеру прямуючому до безмежності, тому границя рівна
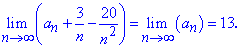
Приклад 31 Обчислити границю функції
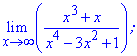
Розв'язання: Виділимо доданок з набільшим показником та розділимо на нього
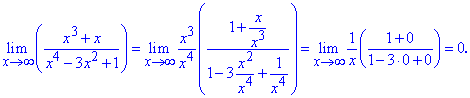
Границя рівна нулю, оскільки степінь змінної в знаменнику більший, аніж в чисельнику.
Приклад 32 Знайти ліміт функції
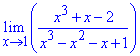
Розв'язання: При підстановці одиниці в дріб отримаємо невизначеність типу {0/0}.
Щоб розкрити невизначеність виділимо в чисельнику і знаменнику множник, що його вносить (x-1).
Для цього розділимо поліноми на вказаний множник.
В результаті отримаємо
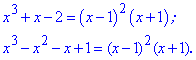
Далі вносимо розклади поліномів в границю та спрощуємо
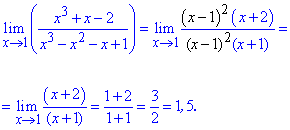
Приклад 33 Знайти границю функцій
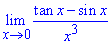
Розв'язання: Для розкриття невизначеності {0/0} скористаємося еквівалентними нескінченно малими ф-ми.
Для цього запишемо по два члени розкладу tan(x), sin(x) в ряд Тейлора (одного недостатньо, в чисельнику отримаємо 0)
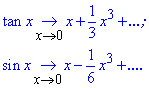
Далі підставимо розклади в границю
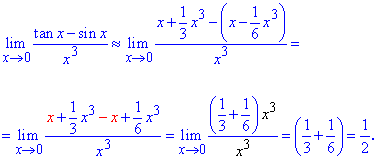
Змінна в кубі спроститься і залишаться сталі, сума яких і шуканою границею.
Приклад 34 Обчислити границю
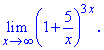
Розв'язання: Зведемо під правило другої важливої границі
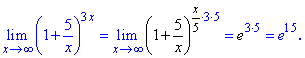
Завдання просте, тому тут немає на чому зупинятися.
Більше відповідей на границі шукайте на сторінках сайту.
