Радіус кривизни траекторії кинутого тіла

Задача 12, 1.31 Камінь кинуто горизонтально зі швидкістю 10 м/с.
Знайти радіус кривизни траєкторії каменя через 3 с після початку руху.

Запишемо формулу для обчислення нормального прискорення: 
,  (*) 
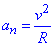де R - радіус кривизни траєкторії каменя в момент часу t.
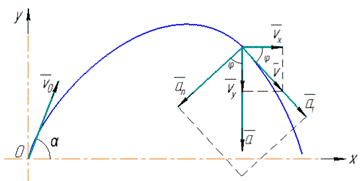
Визначимо напрямки складових швидкостей і повної швидкості v каменя в момент часу t:
vx напрямлене вздовж осі x (горизонтально в напрямку руху), vy напрямлене вздовж осі y (вертикально вниз):  
    ,
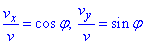де - кут між додатнім напрямком осі x і дотичною до траєкторії каменя в момент часу t.
Визначимо напрямки складових прискорень каменя в момент часу t:
нормальне прискорення a_n напрямлене по радіусу траєкторії до центра кривизни, тангенціальне прискорення 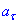напрямлене по дотичній до траєкторії, повне прискорення a=g напрямлене вертикально вниз:  
      
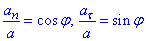
Отримаємо:
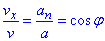, звідси .
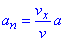Враховуючи (*), отримаємо залежність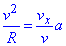 з якої легко виразити радіус кривизни
.

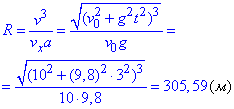Відповідь: R=305,59 м.

Задача 14, 1.37 Тіло кинуто  зі швидкістю 10 м/с під кутом 45⁰ до горизонту.
Знайти радіус кривизни траєкторії через 1 с після початку руху.

Розв'язання: Швидкість каменя v в момент часу t спроектуємо на осі:
вісь x: ;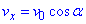   
вісь y: 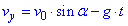,  звідси модуль швидкості

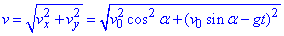
Оскільки камінь падає вільно, то прискорення: a=g.

Обчислимо час, за яке тіло піднімається на найвищу точку траєкторії.
У верхній точці вертикальна складова швидкості відсутня v_y=0, тоді 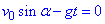, а звідси вже визначаємо час

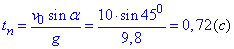
Як бачимо, в момент t=1 с тіло падає вниз.
Запишемо формулу для обчислення нормального прискорення: 
,  (*) 
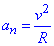де R - радіус кривизни траєкторії каменя в момент часу t.
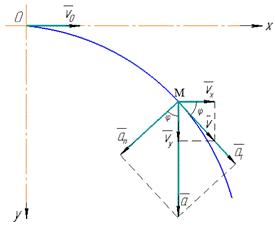
Визначимо напрямки складових прискорень каменя в момент часу t:
нормальне прискорення a_n напрямлене по радіусу траєкторії до центра кривизни, тангенціальне прискорення 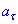напрямлене по дотичній до траєкторії, повне прискорення a=g напрямлене вертикально вниз:  
   
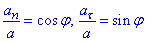
Отримаємо:
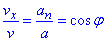, звідси .
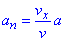Враховуючи (*), отримаємо дробову залежність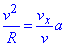,  з якої виражаємо радіус кривизни траекторії
.

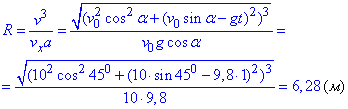Відповідь: R=6,28 м.
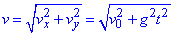