Розв'язування показникових нерівностей

Найпростішу показникову нерівність розв'язують методом зведення до однакової основи двох виразів a^x>a^y (або a^x<a^c):
якщо основа більша одиниці a>1, то, не міняючи знаку, записуємо нерівність для степенів x>y (або x<c відповідно):
a^f(x)>a^g(x)⇔f(x)>g(x); a>1
a^f(x)<a^g(x)⇔f(x)<g(x)
При основі меншій одиниці та більшій нуля 0<a<1, при розкритті нерівність для степенів матиме протилежний знак x<y (або x> y відповідно):
a^f(x)>a^g(x)⇔f(x)<g(x); 0<a<1
a^f(x)<a^g(x)⇔f(x)>g(x)
Дане правило поширюється на випадок нестрогих показникових нерівностей a^x≥a^y, або a^x≤a^с.
Далі перейдемо до готових відповідей ЗНО тестів, але спершу перегляньте графіки та властивості показникових функцій

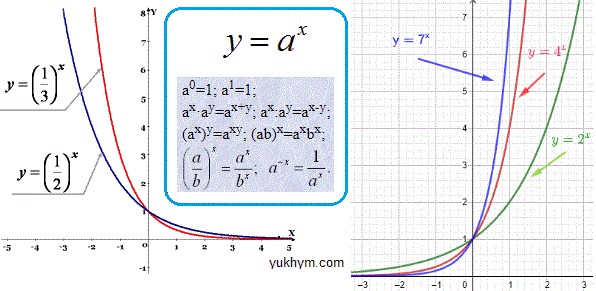
Як бачите, при основах менше одиниці показникова функція спадає з ростом аргументу (графік злва), при більших за одиницю основах характер протилежний, при більших "іксах" маємо більше значення функції. Ви повинні вивчити та знати центральні формули, які вчать як працювати зі степенями.

Приклад 15.7 Розв'язати нерівність 7^x-7^1/x>0.

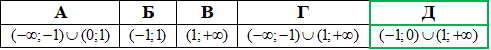
Розв'язування:В показнику маємо змінну в знаменнику, тому спершу випишемо ОДЗ для степеневої функції:
x≠0.
Перенесемо від'ємний доданок в праву сторону нерівності
7^x-7^1/x>0,
7^x>7^1/x.
Оскільки показникова функція 7^x зростаюча, основа більша одиниці 7>1, то, зберігаючи знак нерівності прирівнюємо показники:

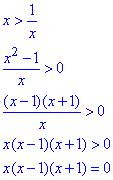
При розв'язуванні рівняння методом інтервалів отримаємо три корені
x₁=-1, x₂=0, x₃=1.
Наносимо їх на числову вісь та методом підставлення точки x=2 визначаємо знак нерівності на крайньому правому інтервалі
x(x-1)(x+1)>0;
2(2-1)(2+1)=6>0.
Отже, справа від точки x=1 нерівність виконується, при переході вліво знаки будуть чергуватися -,+,-

Записуємо інтервали на яких виконуються нерівність:
x∈(-1;0)∪(1;+∞).
Серед ЗНО відповідей правильною є Д.
Відповідь:(-1;0)∪(1;+∞) – Д.

Приклад 15.11 Розв'язати нерівність (1/3)^(x²-x-20)>1.

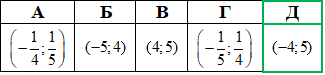
Розв'язування: В показнику маємо квадратичну функцію x²-x-20, основа 1/3 менша одиниці.

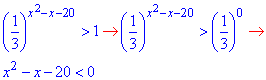
Розв'язки квадратного рівняння
x²-x-20=0
знаходимо за теоремою Вієта:
x₁+x₂=1;
x₁·x₂=20.
Шляхом підбору отримаємо
x₁=-4, x₂=5.
Квадратину нерівність можемо розкласти на прості множники
(x+4)(x-5)<0.
Розв'язуємо кінцеву нерівність методом інтервалів.
Наносимо точки x₁=-4, x₂=5 на числову вісь та методом підстановки точки, наприклад x=0
(0+4)(0-5)=-20<0,
визначаємо, що на інтервалі (-4;5) нерівність виконується.
А це значить, що за його межами будемо мати протилежні знаки "+".

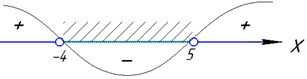
Розв'язок нерівності x∈(-4;5).
Відповідь:(-4;5) – Д.

Приклад 15.13 Знайти множину розв'язків нерівності 4^x-6•2^x+8<0.

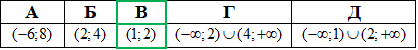
Розв'язування: Показникову нерівність зводимо до квадратної заміною 2^x=t, причому t>0
(2^x)²-6•2^x+8<0,
t²-6•t+8<0.
Крайні точки знайдемо з рівняння
t²-6•t+8=0
за формулами Вієта:
t₁+t₂=6 – сума коренів;
t₁•t₂=8 – їх добуток.

t₁=2, t₂=4 – корені квадратного рівняння.
Розписуємо нерівність через прості множники
(t-2)(t-4)<0
та методом інтервалів визначаємо інтервал де добуток від'ємний

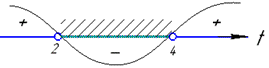
t∈(2;4).
Повертаємося до заміни змінних та обчислюємо прості показникові нерівності


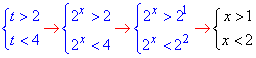
звідси x∈(1;2).
Відповідь:(1;2) – В.

Приклад 15.15 Розв'язати нерівність 3^x+3^2-x>10.

Розв'язування: Групуємо доданки, що містять показникові функції

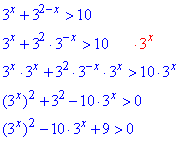
З останньої формули бачимо, що показникову нерівність можна звести до квадратної заміною 3^x=t, причому t>0, тоді
t²-10•t+9>0.
Записуємо квадратне рівняння
t²-10•t+9=0.
та за теоремою Вієта складаємо систему:
t₁+t₂=10 – сума коренів;
t₁•t₂=9 – їх добуток.
Звідси t₁=1, t₂=9 – корені квадратного рівняння.
Переписуємо нерівність (t-1)(t-9)>0
та розв'язуємо методом інтервалів

t∈(0;1)∪(9;+∞).
Повертаємося до заміни змінних та розписуємо прості степеневі нерівності

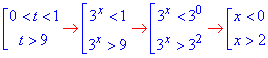
Наносимо точки на числову вісь

та записуємо множину розв'язків x∈(-∞;0)∪(2;+∞).
Відповідь:x∈(-∞;0)∪(2;+∞) – А.

Приклад 15.17 Розв'язати нерівність 3^(|x|+2)>27.

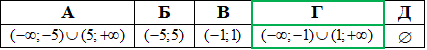
Розв'язування: Зводимо вирази до спільної основи =3, а далі нерівність з модулем замінюємо еквівалентною системою нерівностей

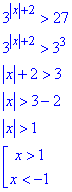
Методом інтервалів

встановлюємо множину розв'язків нерівності x∈(-∞;-1)∪(1;+∞).
Відповідь:(-∞;-1)∪(1;+∞) – Г.

Приклад 15.9 Розв'язати нерівність 1≤(1/3)^x≤27.

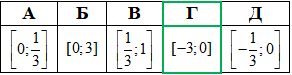
Розв'язування: Зведемо подвійну нерівність до еквівалентної з основою рівною 1/3, а далі замінимо системою нерівностей, які розкриваємо на основі властивостей показникових функцій:

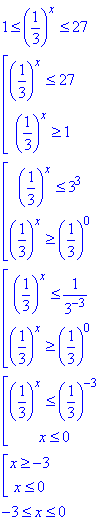
Крайні точки наносимо на числову вісь, нерівність нестрого, тому знайдені точки є розв'язками

Записуємо множину коренів проміжком x∈[-3;0].
Відповідь:[-3;0] – Г.

Наступні завдання рекомендуємо розглядати детально учням, які беруть участь в олімпіадах. Для доброго розуміння, як обчислювати, потрібно поєднувати знання властивостей логарифмічних та показникових функцій.

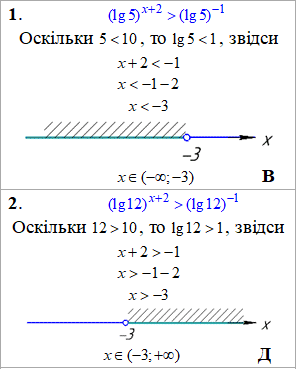
Приклад 15.23 Установити відповідність між нерівностями (1–4) та множинами їх розв'язків (А–Д).

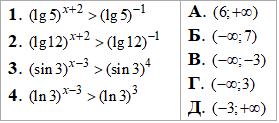
Розв'язування: В основі показникових нерівностей маємо логарифми натуральні, десяткові та в одній синус. Тому згадуємо властивості цих функцій та розкриваємо нерівності. Детальні пояснення до кожного завдання наведені далі в таблицях.

Приклад 15.30 Розв'язати нерівність

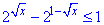
У відповідь записати координату середини проміжку, який є розв'язком нерівності.
Розв'язування: Випишемо ОДЗ кореневої функції:
√x≥0, x≥0.
Далі множимо нерівність на 2^√x

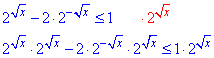
Вираз 2^√x>0 додатний для всіх x, тому множення обох частин нерівності на цей вираз не змінює знаку.
Зводимо до квадратичної нерівності

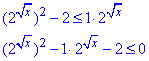
Вводимо заміну:
t=2^√x, де t>0, тоді отримаємо
t²-t-2<0,
t₂-t-2=<0.
За теоремою Вієта складаємо систему рівнянь
t₁+t₂=1,
t₁•t₂=-2,
та знаходимо корені t₁=-1, t₂=2.
Враховуючи умову t>0, одне значення відкидаємо.
Завжди де можна, враховуйте ОДЗ, це дозволить позбутися зайвих коренів та звузити множину на якій ведеться пошук.
Результати переносимо на числову вісь та визначаємо знаки

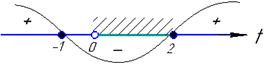
Квадратна нерівність виконується на інтервалі t∈(0;2].
Повертаємося до заміни та розписуємо показникові нерівності

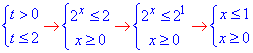
(Починаючи з другої системи нерівностей, врахували ОДЗ x≥0).

x∈[0;1] – розв'язок заданої нерівності.
Обчислимо координати середини знайденого проміжку:
(0+1)/2=0,5.
Відповідь:0,5.

З перегляду пояснень до прикладів Ви могли зауважити, що частини з того що тут викладено Ви вже проходили. Рівняння з модулями, логарифми та квадратні рівняння Ви вчилися розв'язувати в 9, 10 та молодших класах. Тут же йде накопичення та поширення вмінь на новий клас завдань, який в плані обчислень нічим не важчий за попередні задачі. Для багатьох важко дається запам'ятати, що при розкритті показникових нерівностей коли порівнюємо степені слід змінювати знак нерівності на протилежний, якщо основи менші за одиницю. Тому самостійно обчислюйте більше прикладів та переглядайте онлайн готові розв'язки на показникові нервності.