"Знайти дійсні розв'язки рівняння вигляду a*x+b*y+c=0, де a, b, c - комплексні коефіцієнти" – одне з нових завдань в теорії комплексної змінної, яке приводить до розв'язування системи лінійних рівнянь з двома невідомими.
Наведемо методику розв'язання на прикладах, взятих з посібника Тевяшев А.Д., Литвин О.Г., ... "Вища математика в прикладах і задачах." Том 3. Харків 2002 р. Посібники містять багато цікавих задач та їх розв'язки, та рекомендовані Міністерством освіти і науки України для студентів технічних університетів.
Приклади на комплесні числа
Приклад (3.8) Знайти дійсні розв'язки заданих рівнянь
а)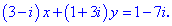
Розв'язання:Розкриємо дужки та перегрупуємо доданки, виділивши дійсну та уявну частину
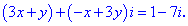
За означенням рівності двох комплексних чисел прирівнюємо дійсну та уявну частини. В результаті отримаємо систему двох лінійних рівнянь
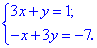
Розв'яжемо отриману систему, для цього з першого рівняння виразимо змінну y та підставимо у друге
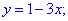
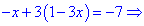
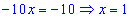
Знайдене значення підставимо в залежність для відшукання y
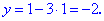
Задане рівняння має розв'язки x=1; y=-2. Схема розв'язування нескладна і після кількох самостійно розв'язаних прикладів Вам добре запам'ятається.
б)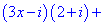 
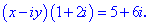
Розв'язання:Перемножимо та згрупуємо подібні доданки
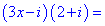
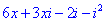
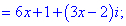
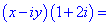
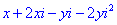
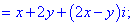
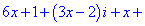
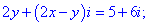
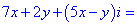
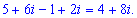
Дане рівняння зводимо до системи лінійних рівнянь
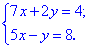
З першого рівняння виражаємо змінну y та підставляємо у друге
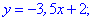
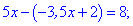
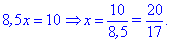
Отримане значення підставляємо в перше рівняння
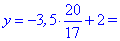
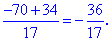
Таким методом отримали наступний розв'язок
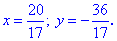
Методика обчислень нескладна і після кількох розглянутих приладів, думаю, Ви зможете повторити обчислення.
Приклад (3.9) Обчислити, за яких дійсних чисел x та y комплексні числа z1 та z2 рівні.
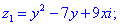
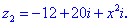
Розв'язання: Прирівнюємо дійсні і уявні частини чисел. В результаті отримаємо два квадратні рівняння
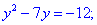
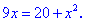
Розв'язуємо кожне з рівнянь для відшукання x та y
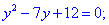
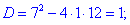
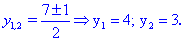
Друге рівняння
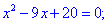
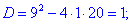
дасть корені 5;4
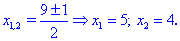
Із знайдених значень отримуємо наступну множину розв'язків
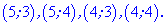
Ось та легко з часом Ви зможете знаходити відповідь до будь-якого завдання, якщо почнети практикувати самостійно.
Приклад (3.10) Визначити, за яких дійсних чисел x та y комплексні числа z1 та z2 спряжені.
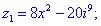
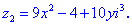
Розв'язання:В даному прикладі потрібно прирівняти дійсну та уявну частину комплексних чисел та врахувати, що для спряжених чисел уявні частини протилежні за знаком. На основі отримаємо
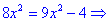
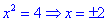
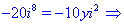
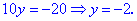
Із знайдених значень сформуємо наступний розв'язок
(-2;2), (2;-2).
При обчисленні подібних прикладів добре вникайте в суть питання: що потрібно знайти ?
В ньому вже міститься підказка - як розв'язати прилад. Решта обчислень пов'язані з властивостями комплексних чисел (множення, піднесення до степеня уявної частини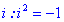 
) і не вимагають складних маніпуляцій. Тож практикуйте з подібними прикладами і поглиблюйте свої знання.
