Позначення: z=f(x, y).
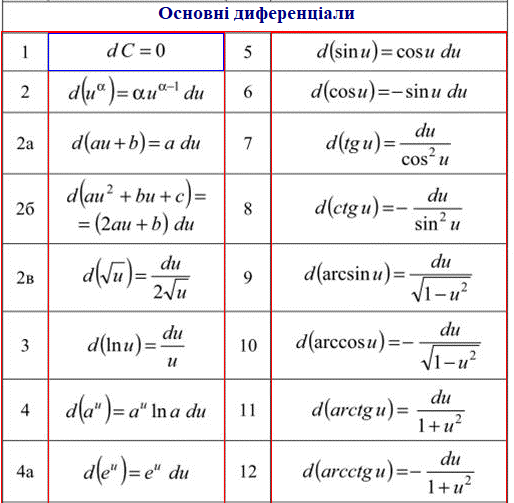
Сукупність пар (x;y) значень x і y, за яких визначається функція z=f(x;y), називається областю визначення, або областю існування цієї функції.
Геометричне місце точок, координати яких задовольняють рівнянню z=f(x;y), називається графіком функцій двох змінних.
Якщо кожній розглядуваній сукупності значень змінних x, y, z, …, u, t із деякої області D (області визначення функції) відповідає єдине значення змінної w, то говорять, що w є функція багатьох незалежних зміннихx, y, z, …, u, t.
Позначення: w=f(x, y, z, …, u, t).
наприклад w=f(x;y;z) - функція трьох змінних і т.д.
Розглянемо точки області D, в яких функція u=f(x;y;z) має постійне значення:
f(x;y;z)=c.
Сукупність цих точок утворює деяку поверхню.
Якщо візьмемо інше значення c, то отримаємо другу поверхню.
Ці поверхні називаються поверхнями рівня.
Якщо функція u є функцією двох змінних x і y, тобто u=f(x;y), то "поверхнями" рівня будуть лінії на площині:
f(x;y)=c, які називаються лініями рівня.
Якщо значення u ми будемо відкладати по осі : z=f(x;y)
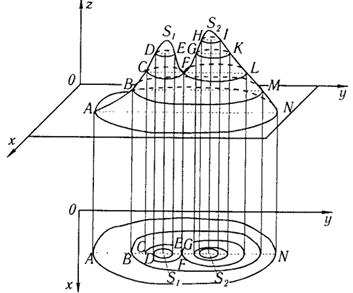
то лініями рівня на площині Oxy будуть проекції ліній, які отримуються в перетині поверхні z=f(x;y) з площинами z=c (рис. 1).
Визначити та зобразити області існування функцій
Приклад 1. u=x+√y.
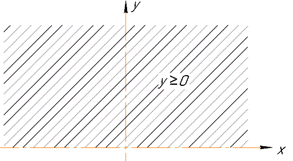
Розв'язування: Оскільки під коренем парного степеня функція набуває невід'ємних значень, то y≥0, тому область існування функції є вся півплощина, що знаходиться вище осі Oy, включаючи й саму вісь.
Приклад 2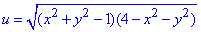 
Розв'язування:Маємо кореневу функцію двох змінних, записуємо умову, що множники під коренем приймають невід'ємні значення та розкриваємо відповідні нерівності
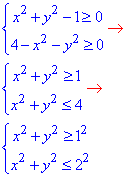
Областю визначення u(x, y) є кільце, що обмежене колами з радіусами R=1 і R=2.
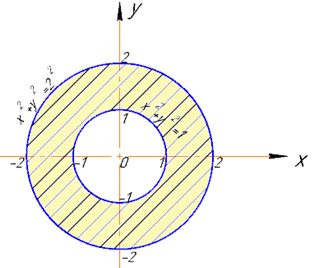
Межі входять в область.
Приклад 3 Знайти та побудувати область визначення u(x, y)
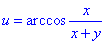
Розв'язування: Арккосинус - обернена тригонометрична функція, що визначена на проміжку [-1;1].
Тому і вираз під арккосинусом має змінюватися в цьому діапазоні. Крім цього знаменник дробу не повинен перетворюватися в0.
Складаємо систему нерівностей
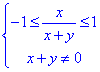
розділяємо її на дві підсистеми
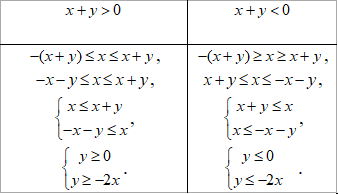
Отримали пару вертикальних тупих кутів, які обмежені прямими y=0 і y=-2x, включаючи цю межу без спільної вершини (0;0).
Будуємо область існування функції u=arccos(x/(x+y)) графічно
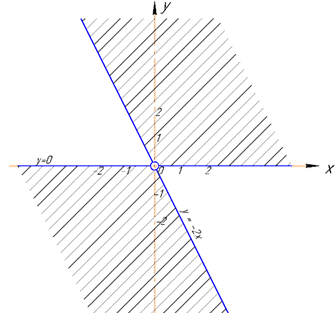
Початок координат не входить в область визначення тому що маємо умову x+y≠0.
Приклад 4 Зобразити область визначення функції трьох змінних
u=ln(1-x2-y2+z2).
Розв'язування: Логарифмічна функція визначена для змінних більших нуля, тому розписуємо відповідну нерівність:
-1-x^2-y^2+z^2>0,
х^2+y^2-z^2<-1.
отримали внутрішність двопорожнинного гіперболоїда.
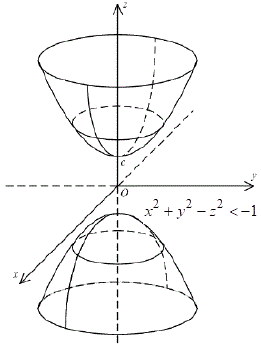
(Збірник задач Б. П. Демидович)
Приклад 5. (3139) Побудувати область існування функції
u=1//√(x2+y2-1).
Розв'язування: Оскільки під коренем парного степеня функція набуває невід'ємних значень, то
x2+y2-1≥0,
x2+y2≥1,
тому область існування функції є зовнішність кола з центром (0;0) та радіусом R=1.
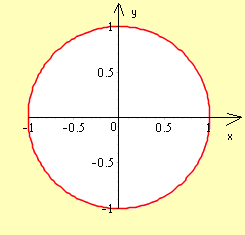
Приклад 6. (3142) Якими кривими обмежена область визначення функції
u=√(1-(x2+y)2).
Розв'язування: Підкоренева функція не повинна приймати від'ємних значень.
З цієї умови отримуємо та розписуємо нерівність.
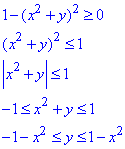
Отримали множину точок площини, яка обмежена параболами y=1-x2 і y=-1-x2.
Приклад 7. (3144)Записати нерівності, що визначають область визначення функції
u=arcsin(y/x).
Розв'язування:Арксинус визначений для аргументів, які за модулем не перевищують одиниці. Крім того, маємо дробову функцію під арксинусом, тому накладаємо додаткову умову на знаменник x≠0.
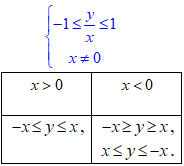
Аналізуючи нерівності, приходимо до висновку, що область існування обмежена парою вертикальних кутів |y|≤|x| (x≠0).
Приклад 8. (3148) Знайти область визначення функції трьох змінних
u=arcos(z/√(x^2+y^2).
Розв'язування:Складаємо систему нерівностей з обмеження на арксинус та знаменник дробу
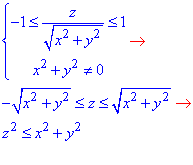
Нерівність z2≤x2+y2 описує зовнішність конуса x2+y2=z2, включаючи межу за виключенням самої вершини (0;0;0).
Далі навчимося будувати лінії та поверхні рівня, знаходити границі та похідні функцій багатьох змінних.
]]>Продублюємо, що таке лінії рівня та перейдемо до практичних де навчимося будувати графіки лінії рівня, зокрема в математичному пакеті Мейпл.
Означення: Якщо функція u є функцією двох змінних x і y, тобто u=f(x;y), то лінії на площині, що задаються рівнянням
f(x;y)=c – називаються лініями рівня.
Побудова графіків ліній рівня
Приклад 1. Побудувати лінії рівня наступних функцій z=x+y,
Розв'язування: Складаємо рівняння ліній рівня та міркуємо, що вони описують
x+y=c,
y=-x+c.
Отримали множину паралельних прямих.
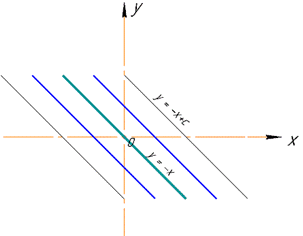
Тут і надалі c - довільна константа.
Приклад 2. Побудувати лінії рівня функції двох змінних
u(x, y)=x2-y2.
Розв'язування: Щоб скласти рівняння ліній рівня прирівнюємо праву сторону до сталої
x2-y2=c.
Дістанемо множину рівносторонніх гіпербол зі спільними асимптотами y=±x, де c≠0.
Схематичний рисунок ліній рівня наведено нижче
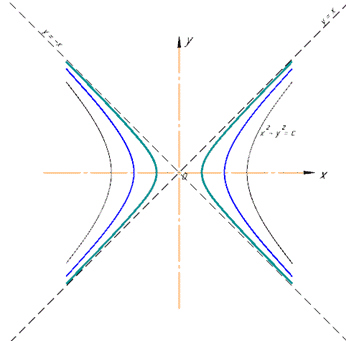
При с=0 асимптоти y=±x стають лініями рівня.
Приклад 3. Зобразити лінії рівня функції
F(x, y)=1/(x2+2y2)
Розв'язування: Прирівняємо праву сторону до сталої та зведемо отримане рівняння до канонічного вигляду
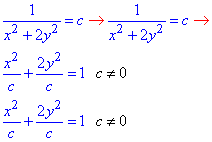
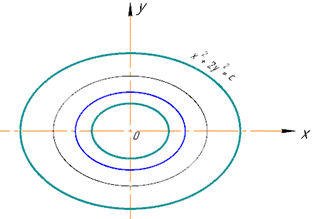
Лініями рівня функції F буде множину подібних еліпсів.
Приклад 4.Схематично зобразити лінії рівня
z=min(x, y).
Розв'язування: Складаємо рівняння та, в залежності від значень аргументу, знаходимо розв'язки
min(x, y)=c,
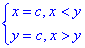
Отримали множину сторін кутів, які паралельні додатнім напрямкам координатних осей Ox і Oy з вершинами на прямій y=x.
Рисунок ліній рівня наступний
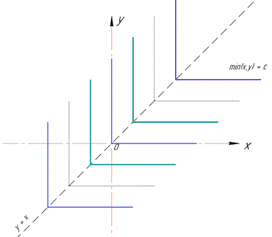
Лінії рівня в Мейпл
Приклад 5. Встановити та зобразити лінії рівня функції
z(x, y)=x2+y2.
Розв'язування: Виписуємо рівняння, яке під силу визначити усім школярам
x2+y2=c.
Отримали множину концентричних кіл з центром в початку координат.
Покажемо як будувати кола в Мейпл
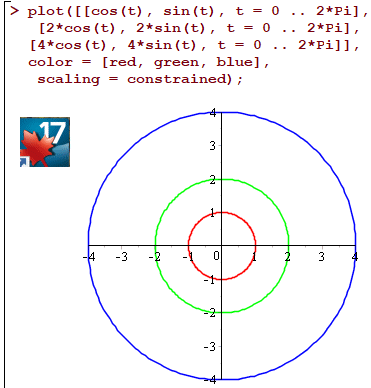
Приклад 6. Визначити лінії рівня функції
z=xy, (x>0).
Розв'язування: Розписуємо рівняння
xy=c,
Логарифмуємо обидві частини
ln(xy)=ln(c),
y•ln(x)=c.
Лініями рівня z(x,y)=xy, (x>0) є множина кривих y=c/ln(x).
Побудуємо графіки в Мейпл для додатних та від'ємних сталих:
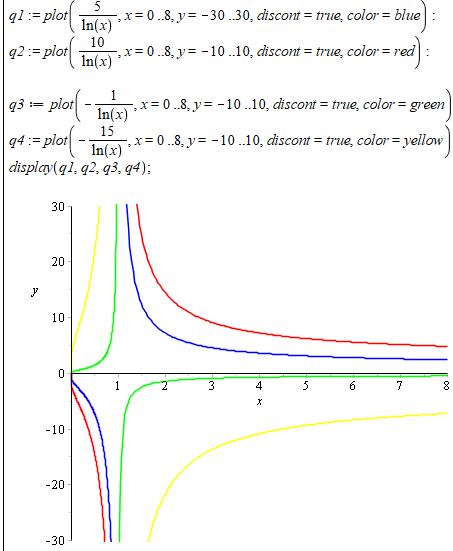
Приклад 7. Знайти та побудувати лінії рівня
z=xye-x.
Розв'язування: Записуємо рівняння лінії рівня та виражаємо з нього y(x,c):
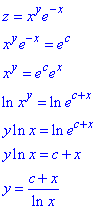
Лініями рівня є множина кривих y=(c+x)/ln(x).
Наведемо код для побудови ліній рівня в Maple
with(plots);
q1 := plot((3+x)/ln(x), x = 0 .. 8, discont = true, color = blue);
q2 := plot((10+x)/ln(x), x = 0 .. 8, discont = true, color = red);
q3 := plot((-5+x)/ln(x), x = 0 .. 8, discont = true, color = green);
display(q1, q2, q3);
Тут команда with(plots); підключає бібліотеку для роботи з графікою
display - виводить кілька графіків одночасно.
discount - функція, яка дозволяє будувати графік неперервно, або з асимптотами (розривно).
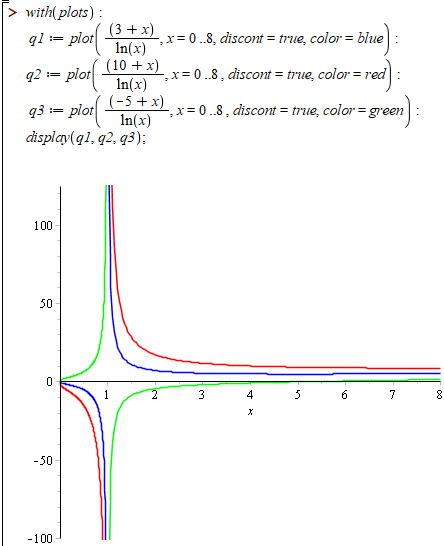
Приклад 8. Побудувати лінії рівня функції двох змінних
z(x, y)=√x√y.
Розв'язування: Прирівнюємо функцію до сталої та виражаємо y(x)
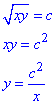
Лініями рівня є множина рівносторонніх гіпербол, які знаходяться в І і ІІ квадрантах, асимптотами є осі координат Ox і Oy.
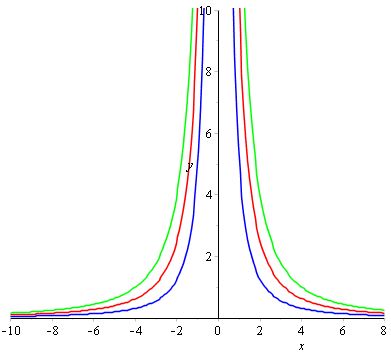
Наведемо код в Мейплі для побудови графіка
q1 := plot(5/x^2, x = -10 .. 8, y = 0 .. 10, discont = true, color = blue);
інші 2 криві для с2=10 та с2=16.
Далі навчимо Вас будувати поверхні рівня та обчислювати границі та екстремуми функцій багатьох змінних.
f(x,y,z)=C=const.
На практиці визначення поверхні рівня зводиться до прирівняння функції трьох змінних до сталої, далі, якщо є можливо, вираженні однієї з координат через дві інші та сталу. В загальному поверхня рівня – це просторовий об'єкт і лише в часткових випадках отримаємо площини.
На практичних, особливо де потрібно побудувати графік поверхні рівня, Вам не задаватимуть чогось надзвичайного.
Достатьно знати рівняння площини та кілька фігур обертання, зокрема як будувати сферу, циліндр, конус (гіперболоїд, параболоїд, тор).
В природі до поверхонь рівня відносяться поверхні рівної температури, рівного тиску, вологості. Наприклад для краплі води поверхнею рівня буде поверхня, що межує з повітрям (форма каплі, що бачимо).
Приклад 1. Побудувати поверхні рівня функції
u=x+y+z.
Розв'язування: Виписуємо рівняння поверхні рівня
x+y+z=c.
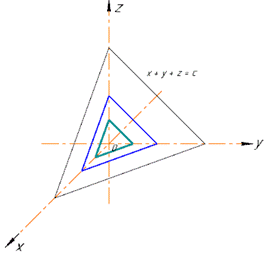
При зміні сталої отримаємо множину паралельних площин, рівнонахилених до напрямку координатних осей.
Схематично покажемо, як перетинають ці поверхні координатні площини.
Приклад 2. u=x^2+y^2-z^2.
Розв'язування: Записуємо рівняння повехні рівня
x2+y2-z2=c.
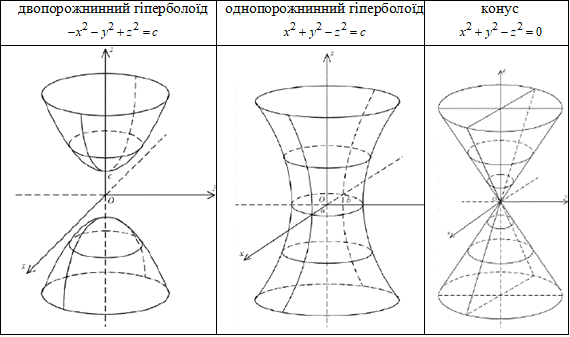
Отримали множину двопорожнинних гіперболоїдів при u<0;
множину однопорожнинних гіперболоїдів при u>0;
конус при u=0.
Таблицю з рисунками можливих поверхонь рівня наведено нижче
Приклад 3. Визначити поверхню рівня функції
u=(x-5)2+(y-3)2+(z-7)2.
Розв'язування: Складаємо рівняння поверхні рівня
(x-5)2+(y-3)2+(z-7)2=c.
З рівняння бачимо, що це множина концентричних сфер з центром в точці (5;3;7).
Приклад 4. Cкласти поверхню рівня та визначити її вигляд
u=(x+y)2+z2.
Розв'язування: За наведеним вище алгоритмом записуємо
(x+y)2+z2=c
Формула описує множину еліптичних циліндрів, спільною віссю яких є пряма x+y=0, z=0.
Приклад 5. Побудувати поверхню рівня функції
u=z-ln(x+y)·(x2-y).
Розв'язування: Прирівнюємо праву сторону до сталої
z-ln(x+y)·(x2-y)=c.
При с=0 будемо мати
z=ln(x+y)·(x2-y)
Побудуємо поверхню рівня в Мейплі
plot3d(ln(x+y)*(x^2-y), x = 0 .. 5, y = 0 .. 6) ;
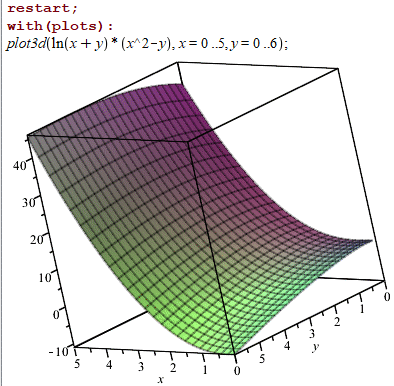
При інших сталих c поверхня буде зміщатися вгору або вниз по осі Oz.
Подібних прикладів можна привести безліч, Вам головне з уроку знати, що таке поверхня рівня, і уявляти як геометрично виглядають простіші із них.
]]>Приклад 1. Знайти f(1,y/x), якщо f(x,y)=2xy/(x2+y2)
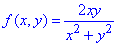
Розв'язування: Нехай маємо
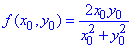
Тоді за умовою, замінюємо першу координату на x0=1, другу – на y0=y/x.
Отримаємо:
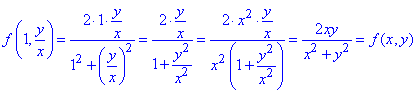
Думаю такий тип завдань Ви зможете виконати самостійно.
Приклад 2. Нехай z=√y+f(√x-1)
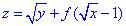
Знайти функції f і z, якщо z=x при y=1.
Розв'язування: Перегляньте прийоми викорастані для вираження функції f(x).
Підставимо в рівняння
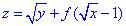
значенння з умови z=x при y=1.
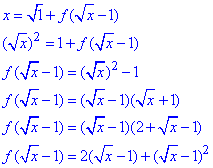
переходячи до нової змінної t=√x-1, отримаємо
f(t)=2t+t2.
Враховуючи умову z=√y+f(√x-1) і нову зміну t=√x-1, запишемо
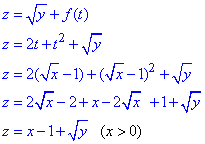
Приклад 3. Знайти f(x,y), якщо f(x+y,y/x)=x2-y2.
Розв'язування: Виконаємо певні маніпуляції зі змінними, щоб перейти до потрібних
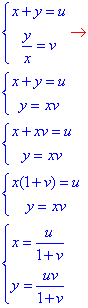
Підставимо отримані вирази в задану функцію:
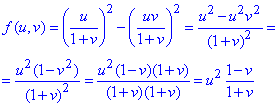
Переходячи до змінних x і y, отримаємо остаточно
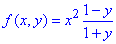
Всіх перетворень тут не виписували, тому переконайтесь самостійно, що кінцева формула буде такою.
Приклад 4. Знайти f(x), якщо f(y/x)
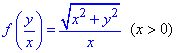
Розв'язування: Виконуємо елементарні перетворення в правій частині, щоб добитися вигляду функції від y/x:
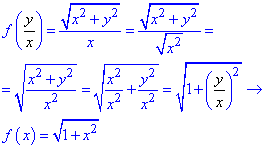
Приклад 5. Нехай z=x+y+f(x-y).
Знайти функції f і z, якщо z=x^2 при y=0.
Розв'язування: Підставимо значення з умови в функцію
x2=x+0+f(x-0),
звідси f(x)=x2-x.
Враховуючи умову z=x+y+f(x-y), запишемо
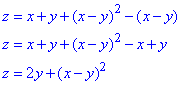
Подібні приклади Ви не один раз зустрінете при вивченні функцій багатьох змінних. Які заміни змінних чи переходи слід виконувати ми тут розглянули. Єдине, що можемо порадити, вчіться розв'язувати самостійно.
Лише перечитуванням готових розв'язків Ви успіху в математиці не досягнете!
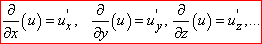
При обчисленні похідних інші змінні не залежать від тієї по якій диференціюємо, і так для кожної змінної.
Частковими похідними другого порядку функції двох змінних u(x;y) називається їх часткові похідні від часткових похідних першого порядку.
Позначення других часткових похідних:
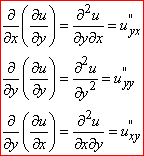
Для функції трьох змінних до цих формул добавиться друга похідна по z та дві мішані похідні по xz та yz.
Аналогічно визначаються похідні вищих порядків, наприклад
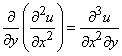
і т.д.
Частинні похідні, які відмінні одна від одної лише порядком диференціювання, називаються мішаними похідними;
вони є рівними між собою при умові, що неперервні в деякому околі точки M.
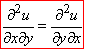
Далі наведемо приклади з практики студентів, які Вас можуть чекати. Перегляньте обчислення та оформлення завдань на похідні функцій u(x;y).
Знайти часткові похідні першого і другого порядку функції двох змінних
Приклад 1. u=x4+y4-4x2y2.
Обчислення: Пояснювати, як брати похідні тут не будемо. Для цього на сайті є окремий розділ, який вчить знаходити похідні.
Знаходимо часткові похідні І порядку: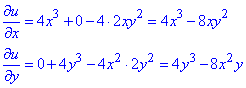 
Часткові похідні II порядку: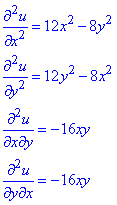 
Оскільки сама функція u(x;y) і її часткові похідні першого порядку неперервні на всій області визначення, то мішані похідні рівні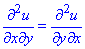
.
Приклад 2. u=x/y2.
Обчислення: Часткові похідні І порядку: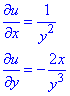 
Часткові похідні II порядку: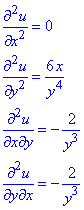 
Мішані похідні співпадають, оскільки функція u(x,y) з її похідними першого порядку неперервна на всій області визначення.
Ви можете заперечувати таз огляду на вигляд u=x/y2 стверджувати, що функція розривна при y=0, але ця точка не входить в область визначення, а всюди поза точкою ф-я неперервна і диференційовна.
Приклад 3. u=x•sin(x+y).
Обчислення: Часткові похідні І порядку: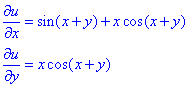 
Часткові похідні II порядку: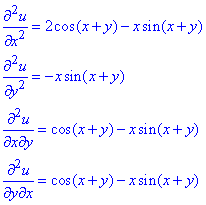 
Мішані похідні рівні між собою.
Приклад 4. u=tan(x2/y2).
Обчислення: Уважно перегляньте правила похідних від складених функцій, це спростить обчислення цього та наступних за ним прикладів.
Часткові похідні І порядку: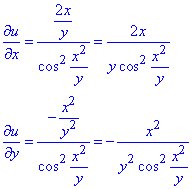 
Часткові похідні II порядку: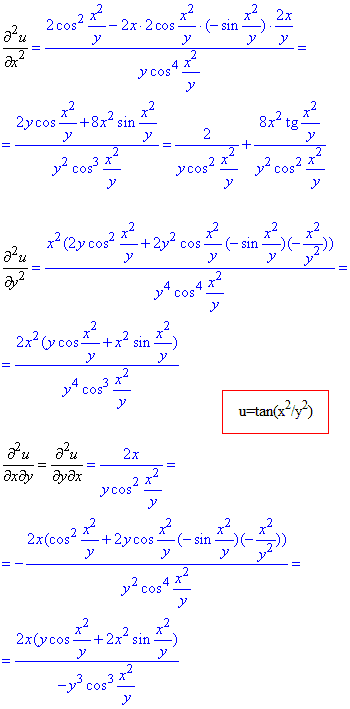 
Приклад 5. u=ln(x+y2).
Обчислення: Часткові похідні І порядку: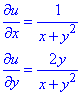 
Часткові похідні II порядку: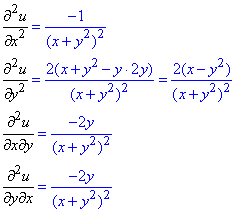 
Як бачимо мішані похідні співпадають.
Приклад 6.Знайти похідні першого та другого порядку функції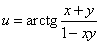
Обчислення: Часткові похідні І порядку: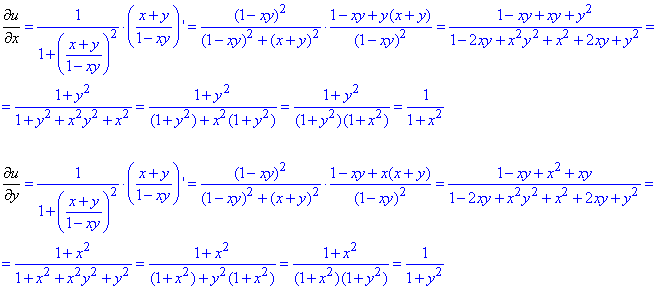 
Часткові похідні II порядку: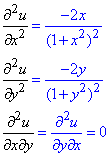 
Часткові похідні І порядку можна віднайти набагато легше, якщо впізнати формулу з обернених тригонометричних функцій: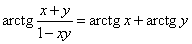 
Приклад 7 (2.2) T=π√(l/g). Показати, що
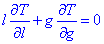
Обчислення: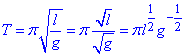
Знаходимо часткові похідні І порядку: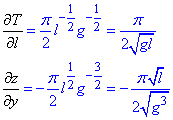 
Підставимо отримані похідні у задане диференціальне рівняння: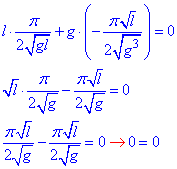 
Отримали тотожність, тому задана функція 1 є розв'язком рівняння 2.
Приклад 8 (3.1) {x=ρ•cos(φ), y=ρ•sin(φ)}.
Обчислити визначник складений з часткових похідних
Обчислення: Визначаємо часткові похідні І порядку: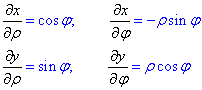 
Підставимо отримані похідні у заданий визначник і обчислимо його: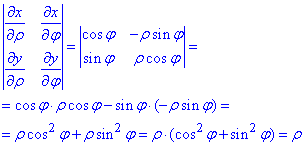 
Цей визначник є якобіаном переходу від декартових до полярних координат, і його неодноразово будете бачити в інтегруванні.
Приклад 9. Знайти часткові похідні I та II порядку.
u=1/√(x2+y2+z2).
Обчислення:Спершу перетворимо функцію для зручності брати похідну
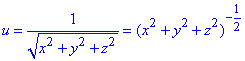
Знаходимо часткові похідні І порядку за правилом похідної складеної функції: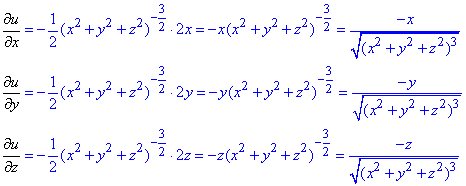 
Далі часткові похідні II порядку: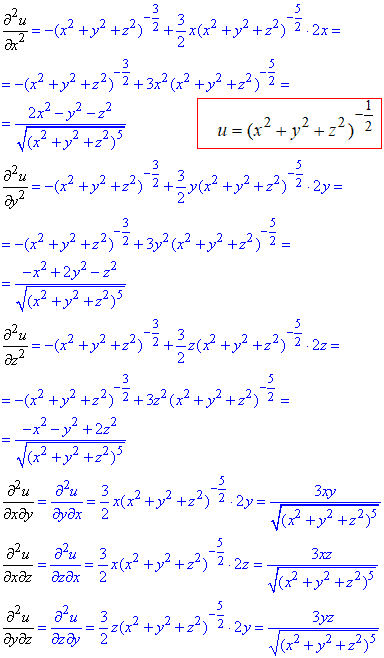 
З коренями не всім легко даються похідні, тому будьте уважні при обчисленнях.
Приклад 10. Знайти перші та друг часткові похідні
u=x^(y/z).
Обчислення: Часткові похідні І порядку: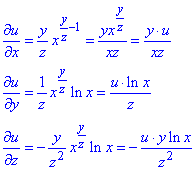 
Часткові похідні II порядку: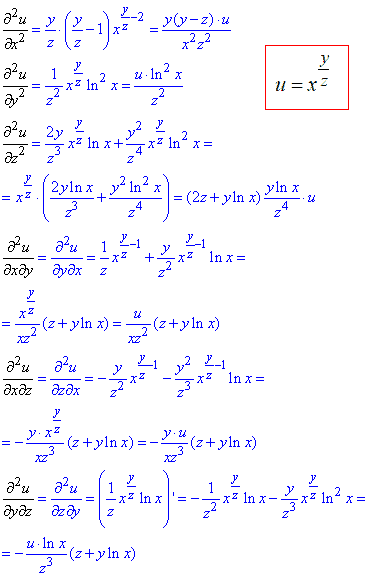 
Часткові похідні потрібні для дослідження функцій багатьох змінних, пошуку точок екстремуму, перегинів, обчислення диференціалів, значення похідних в точці.
Все поступово навчимося виконувати з наступних уроків.
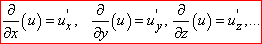
чи другого порядку
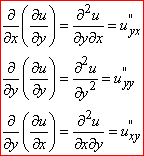
Третя часткова похідна утворюється диференціюванням похідних другого порядку, четверта часткова похідна – обчисленням похідних від похідної 3 порядку за змінними
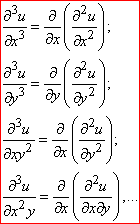
і т. д.
На практиці рідко просять знайти похідні вище 5 порядку, виняток становлять завдання з експонентами та тригонометричними ф-ми, де легко вловити закономірність обчислення похідних.
Почнемо з простіших завдань, які не увійшли до попереднього уроку, а далі важчі.
Приклад 1. Знайти частинні похідні першого та другого порядку
u=cos(x3+y2)
Обчислення: Часткові похідні І порядку:
∂u/∂x=-3x2·sin(x3+y2);
∂u/∂y=-2y·sin(x3+y2).
Часткові похідні ІІ порядку:
∂2u/∂x2=∂u/∂x(-3x2·sin(x3+y2))=
= -6x·sin(x3+y2)-9x4·cos(x3+y2);
∂2u/∂y2=∂u/∂y(-2y·sin(x3+y2))=
= -2·sin(x3+y2)-4y2·cos(x3+y2);
∂2u/∂y∂x=∂u/∂y(-3x2·sin(x3+y2))=
= -6yx2·cos(x3+y2).
На сайті постійно вивчаємо математичні пакети, тому покажемо як 1 та 2 часткові похідні обчислювати в мейплі
f := cos(x^3+y^2);
d_x := diff(f, x);
d_y := diff(f, y);
d_xx := diff(f, x, x);
d_yy := diff(f, y, y);
d_xy := diff(f, x, y);
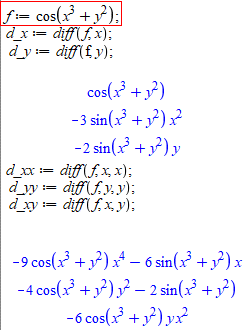
Змінюємо функцію і маємо готовий калькулятор часткових похідних
Приклад 2. Знайти часткові похідні третього порядку ∂3f/∂x3,∂3f/∂y3
f=exp(y+x2)
Обчислення:Експоненту легко як інтегрувати так і диференціювати.
Не забуваємо, що маємо складену функцію та знаходимо часткові похідні 1-3 порядку
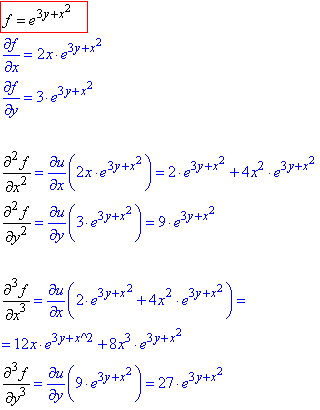
Перевіримо їх в Мейплі, заодно обчислимо мішані похідні третього порядку.
Для цього до вище виписаного коду додамо третю часткову похідну
d_xxx := diff(f, x, x, x);
d_yyx := diff(f, y, y, x);
d_yxx := diff(f, y, x, x);
d_xxx := diff(f, y, y, y)
В результаті отримаємо
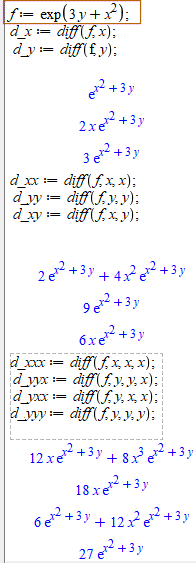
При наборі формул теж слід уважно дивитися, щоб не допустити помилок.
Приклад 3 (2.1) z=ln(x2+xy+y2).
Показати, що має місце рівняння в частвових похідних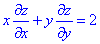
Обчислення: Часткові похідні І порядку: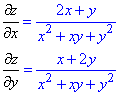 
Підставимо отримані похідні у задане диференціальне рівняння: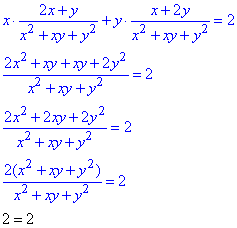 
Отримали тотожність, тому задана функція є розв'язком рівняння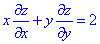 
що і треба було довести.
Приклад 4 (4.1) Задана функція двох змінних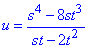
Знайти третю похідну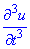
у точці (-1;1).
Обчислення: Часткові похідні І порядку: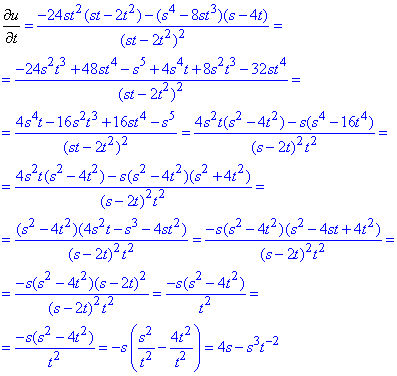 
Часткові похідні ІІ порядку: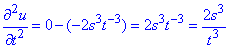 
Часткові похідні ІІІ порядку: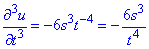 
Обчислимо часткову похідну 3 порядку у точці (-1;1).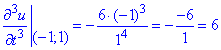 
Якщо попередньо спростити вираз функції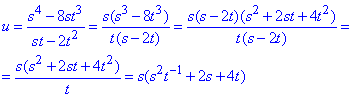
то відшукання часткової похідної І порядку стає легким.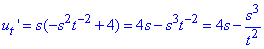 
Відповідно і похідні вищих порядків легше знаходити.
Приклад 5 (4.2) z=x4+x3y+x2y2+xy3+y4.
Знайти частинні похідні четвертого порядку.
Обчислення: У функціях подібного виду похідна вищого порядку береться лише від виразів, у яких змінні мають степінь не нижче порядку похідної по кожній змінній, решта – нулі, оскільки на певних етапах вони стають константами, а похідна від сталої рівна 0.
Знаючи це правило, можемо записати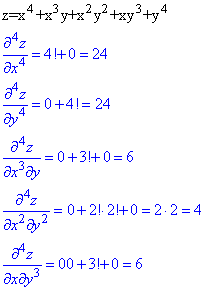
Спробуйте перевірити самостійно.
Приклад 6 (4.3) Знайти четверті похідні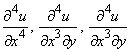
якщо функція має вигляд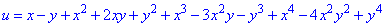
Обчислення: Нагадуємо правило, що у многочленах з кількома змінними похідна вищого порядку береться лише для виразів, змінні яких мають степінь, який рівний або вище порядку похідної по кожній змінній, решта – нулі. Це тому, що після ряду диференціювань залишаються тільки сталі.
Тому аналізуючи вигляд ф-ї, отримаємо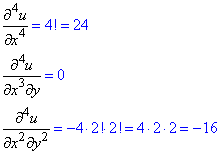 
Для перевірки розв'яжіть це завдання самостійно.
Нехай задана функція u=f(x;y;z), яка диференційовна в кожній точці області визначення. Тоді для неї існує повний диференціал:
Диференціал І порядку
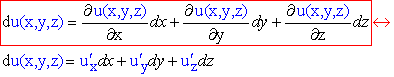
Диференціал II порядку та старших
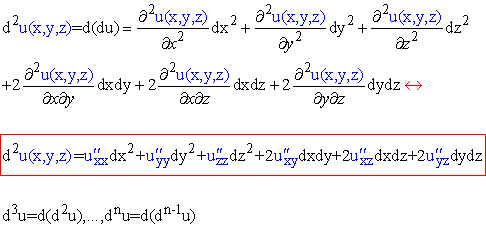
Поклавши одну зі змінних рівною нулю отримуємо формули повних диференціалів для функції двох змінних
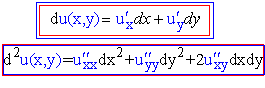
Правила диференціювання суми, добутку, та частки функцій
Якщо функції u(x,y,z), v(x,y,z) - диференційовні на області визначення, то справедливі формули
Якщо маємо складені функції наступного виду, то їх відповідні диференціали можна знайти за формулами:
Наприклад, для функції u=ex+y за формулою 4а диференціал першого роду рівний
du=d(ex+y)=ex+y·d(x+y)=ex+y·(dx+dy),
диференціал 2 роду обчислюємо за правилом
d2u=d(du)=d(ex+y·(dx+dy))=ex+y·dx2+2ex+ydxdy+ex+ydy2.
Для функцій багатьох змінних має місце інваріантність форми (першого) диференціала, як і для функції однієї змінної!
Далі розберемо готові розв'язки з практичних, які Ви повинні знати як робити та оформляти. Основні формули потрібні для обчислень будуть підкреслені червоним прямокутником.
Знайти диференціали першого і другого порядку f(x, y)
Приклад 1.1 u=xm∙yn, (x, y - незалежні змінні)
Обчислення: Степеневу функцію не важко диференціювати.
Знаходимо диференціал І порядку:
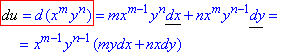
Диференціал II порядку: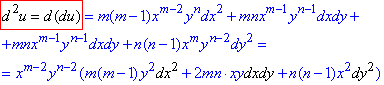 
Приклад 1.2 д u=x/y.
Обчислення: Перегляньте, як знаходити диференціали обернених функцій: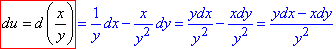 
Для порівняння можете зіставити з формулою (5) правил обчислення диференціалів, що наведені на початку уроку в таблиці.
Диференціал II порядку: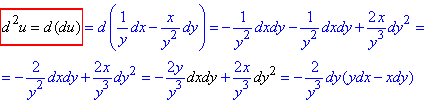 
Правила, що тут виділені у формулах Вам допоможуть швидко засвоїти теоретичний матеріал.
Приклад 1.2 u=√(x2+y2).
Обчислення: Диференціал 1 порядку для кореневої функції обчислюємо за формулою 2в: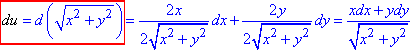 
Диференціал 2 порядку: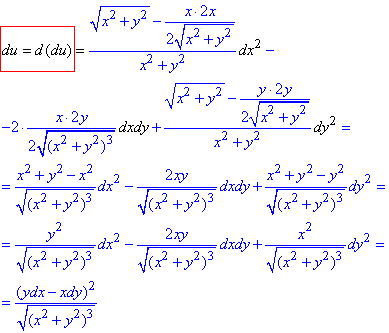 
Приклад 1.3 u=exp(xy)
Обчислення: Знаходимо диференціал І порядку від експоненти :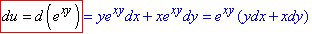 
Щоб знати диференціал II порядку повторно диференціюємо du: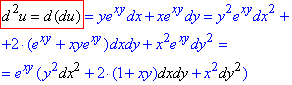 
Приклад 1.4 Знайти диференціали першого та другого порядку функції трьох змінних
u=z/(x2+y2).
Обчислення: Диференціал І порядку: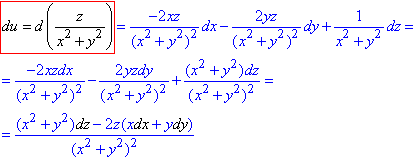 
Частинні похідні можна перевіряти в математичних пакетах, зокрема в Мейплі код для похідних за змінними має вигляд:
u := z/(x^2+y^2);
d_x := diff(u, x); d_y := diff(u, y); d_z := diff(u, z);
В результаті отримаємо складові диференціалу першого порядку
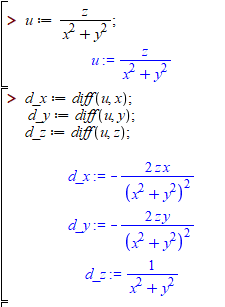
Щоб знайти диференціал II порядку повторно диференціюємо du за трьома змінними, після чого групуємо подібні доданки: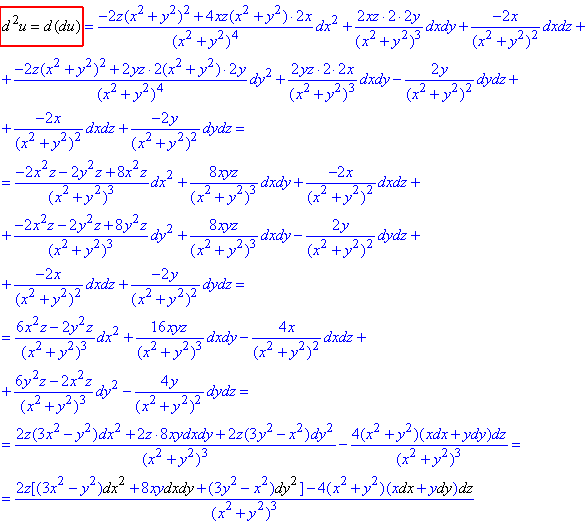 
Щоб не помилитись при обчисленні d2u розбийте перший диференціал на три доданки, а далі кожен з них диференціюйте за кожною зі змінних. Після того групуєте доданки при однакових парах dx2, dy2,dz2,dxdy, dxdz, dydz.
Ця методика справедлива і для функції багатьох змінних.
]]>
Якщо задана диференційовна функція трьох змінних u=f(x;y;z) то повний диференціал обчислюють за формулами:
Диференціал І порядку
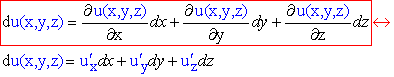(1)
Диференціал II порядку та старших
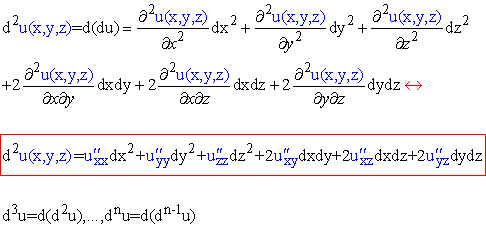(2)
Як знайти частинні похідні вчили на попередніх уроках і продовжимо тут, це всього навсього звичайні похідні за конкретними змінними, при цьому решту змінних в функції вважаємо незалежними від тієї, по якій обчислюємо похідну.
Формули повних диференціалів для функції двох змінних u=f(x, y):
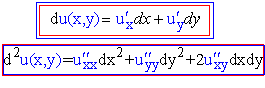(3)
Оскільки для обчислення диференціалів вищих порядків необхідно знайти диференціал на порядок нижче
dnu=d(dn-1u), (4)
то і перший і другий диференціали будемо тут знаходити.
Наведемо формули основних диференціалів, щоб постійно не звертатися до таблиці похідних
Переходимо до практичних з яких навчимося, як знайти повний диференціал другого та вищих порядків.
Приклад 2.1 Обчислити перший та другий диференціали
u=cos(x+y2)
Обчислення: За формулою (6) таблиці основних диференціалів розписуємо
du=d(cos(x+y2))=-sin(x+y2)d(x+y2)=-sin(x+y2)dx-2y∙sin(x+y2)dy.
Щоб знайти другий диференціал застосовуємо формулу (3)
d2u=-cos(x+y2)dx2-4y∙cos(x+y2)dxdy-4y2∙cos(x+y2)dy2
Приклад 2.2 Знайти диференціал третього порядку d3u, якщо u=x3+y3-3xy(x-y)
Обчислення: Розпишемо функцію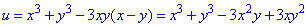
Складемо диференціал І порядку за формулою (3):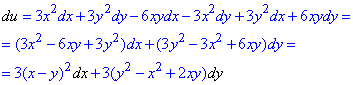 
Диференціал II порядку: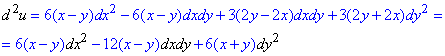 
Обчислення: Диференціал IIІ порядку: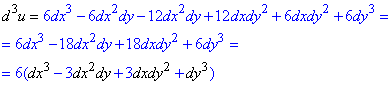 
Приклад 2.3 Обчислити десятий диференціал d10u, якщо u=ln(x+y)
Обчислення: Диференціал І порядку: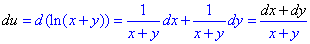 
Диференціал II порядку: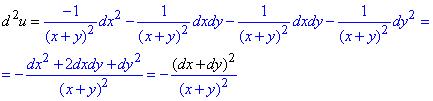 
Диференціал IIІ порядку: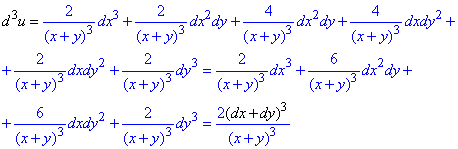 
Аналізуючи формули диференціалів першого - третього порядку вловлюємо закономірність, яка дозволяє виписати формулу
диференціалу IV порядку: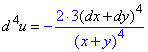 
та старших.
Диференціал n-го порядку: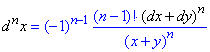 
Звідси диференціал X порядку: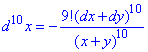 
Приклад 2.4 Знайти третій диференціал d3u, якщо u=xyz.
Обчислення: Диференціал І порядку:
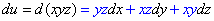
Диференціал ІI порядку: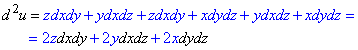 
Диференціал ІII порядку: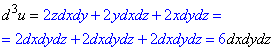 
Приклад 2.5 Визначити dnu, якщо u=exp(a∙x+b∙y).
Обчислення: Диференціал І порядку: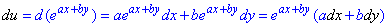 
Диференціал ІI порядку: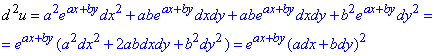 
Диференціал ІII порядку: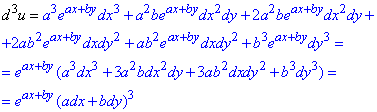 
Диференціал n-го порядку: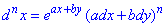 
Якщо маєте труднощі з обчисленням повних диференціалів другого чи вищих порядків, не знаєте як знайти похідні складених функцій, можете звертатись за допомогою або консультацією.
На практичних Вам потрібно знати або мати перед очима таблиці похідних, далі вміти їх застосувати для обчислення частинних похідних, а вже скласти формулу деренціалів функцій не важко.
x=φ(t), y=ψ(t), z=χ(t).
Нехай, крім того, при зміненні t точки (x;y;z) не виходять за межі області D.
Підставимо значення x, y, z у функцію u=f(x;y;z), отримаємо складену функцію: u=f(φ(t),ψ(t),χ(t)).
Нехай u має по x, y, z неперервні часткові похідні u'x, u'y, u'z
і похідні за змінною t
x't, y't, z't
існують.
Тоді справедливі формули похідної складеної функції:
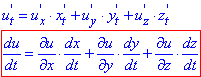(1)Тепер розглянемо випадок, коли x, y, z залежать не від однієї змінної t, а від декількох змінних, наприклад
x=φ(t;v), y=ψ(t;v), z=χ(t;v).
Тоді маємо формули частинних похідних складених функцій:
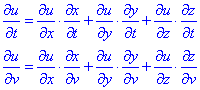(2)
Також для вивчення теми Вам буде потрібна таблиця похідних, тому її тут приведемо, а Ви її краще видрукуйте та майте перед очима.
Приклад 1.1 Знайти dz/dt, якщо
z=ex+y2, де x=ln(t), y=sin(t).
Обчислення: Застосовуємо формулу (1) для складеної функції z:
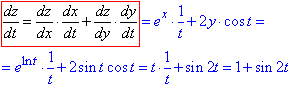
Приклад 1.2 Знайти dz/dt, якщо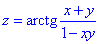
де x=tan(t),y=-ctg(t).
Обчислення: З таблиці похідних беремо формули похідних арктангенса (22), тангенса (16) і котангенса (11), та розписуємо добуток похідних за формулою для складених функцій (1)
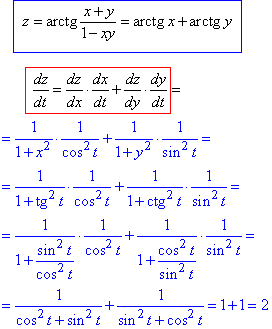
Приклад 1.3 Визначити dz/dt, якщо
z=exp(2x-3y), де x=tg(t), y=t2-1.
Обчислення: Не забуваємо, що тут експонента має складний аргумент, тому формула (11) не підійде, а якщо її і використовувати, то додатково потрібно домножити на похідну від (2x-3y) за змінною.
Перегляньте як знаходили похідну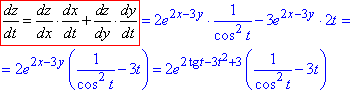 
Приклад 1.4 Обчислити dz/dt, якщо z=arcsin(x-y), де x=3t,y=4t3.
Обчислення:Похідну від арксинуса обчислюємо за формулою (20)+домножуємо на похідні від аргументів, оскільки функція складена. Далі все це множимо на похідні від змінних за (1) формулою
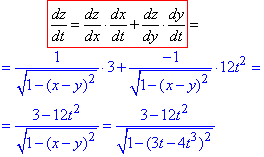
Приклад 1.5Знайти dz/dt, якщо z=arctg(x/y), де x=e2t+1, y=e2t-1.
Обчислення: Не забуваємо, що під арктангенсом складений аргумент, тому застосовуємо формули (22), (24).
А оскільки аргументи є також функціями параметра t, то похідні експонент знаходимо за (11) ф-лою, а вже dz/dt розписуємо згідно (1):
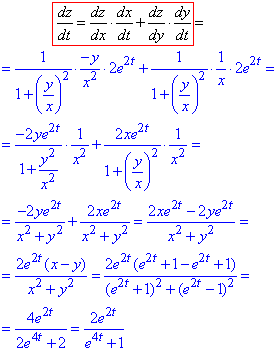
Все решта, це зведення до спільного знаменника та підставлення x(t), y(t), щоб похідна була залежна тільки від параметра dz/dt=z't(t).
Диференціал складених функцій
Приклад 2.1 Знайти диференціал dz для функції z=f(u,v), якщо u=cos(x∙y), v=x5-7y.
Обчислення: Тут аргументи функції u, v є функціями двох аргументів, тому застосовуємо формулу (2) для знаходження диференціалу функції
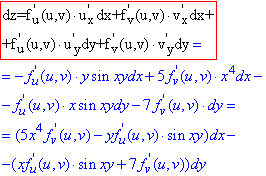
Оскільки z задана неявно, то це дещо спрощує як обчислення, так і читання формули диференціалу.
Частинні похідні від складених функцій Ви повинні вміти брати, якщо ні, то можете переглянути уроки на похідні.
Приклад 2.2 Знайти dz для функції z=f(x, y, t), якщо x=u+v, y=u2+v2, t=u∙v.
Обчислення: Тут маємо функцію трьох змінних, аргументи якої є функціями ще 2 змінних, тому формула диференціалу міститиме на 2 доданки більше за попередній приклад. Записуємо формулу диференціалу та підставляємо відповідні похідні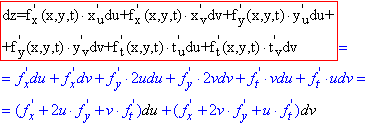
Далі групуємо часткові диференціали.
Приклад 2.3 Обчислити dz, якщо z(x, y) має вигляд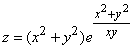
Обчислення: Функція задана в явному виді та містить дві змінні, тому її диференціал знаходимо за формулою
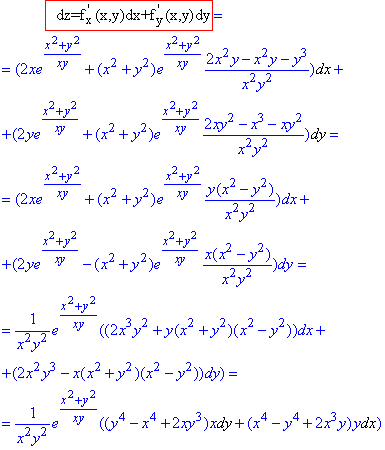
При обчисленні слід врахувати правило добутку. Наостанок згрупували доданки та винесли експоненту як множник, щоб отримати компактний вираз диференціалу.
Далі розв'яжемо приклади на похідні неявно заданих функцій багатьох змінних.
крім цього, в цій точці F'y(x;y)≠0.
Тоді похідна y від x:
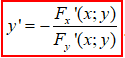(1)Для відшукання часткових похідних ∂z/∂x, ∂z/∂x від функції F(x;y;z) мають місце наступні формули:
(2)
На попередньому уроці вчили знаходити похідні складених функцій 2, 3 змінних і таблиця похідних була потрібна. Цього разу тема дещо легша, але таблицю похідних продовжимо вивчати та застосовувати.
Приклад 3.1 Знайти похідну dy/dx від функцій, заданих рівнянням
x2y+xy2-y3-1=0.
Обчислення: Похідні неявних функцій будемо визначати за (1) формулою, тому спершу записуємо неявне рівняння як функцію, далі беремо часткові похідні та застосовуємо формулу (виділена прямокутником).
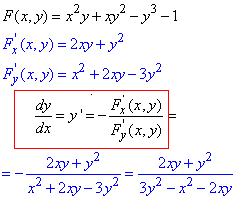
Як Ви могли переконатися, це легші завдання в порівнянні з параметрично заданими функціями.
Приклад 3.2 Знайти похідну dy/dx неявно заданої функції
x∙ey+y∙ex-exy=0.
Обчислення: Повторюємо алгоритм похідної неявної функції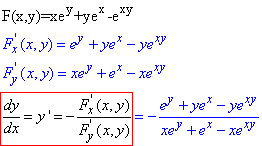
Тут більше спрощувати немає чого.
Приклад 3.3 Знайти похідну dy/dx функції
x2/3+y2/3=a2/3.
Обчислення: Переносимо сталу за знак рівності та застосовуємо формули похідної для неявно заданої функції та (8) з таблиці похідних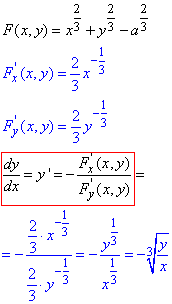
У Вас може виникнути запитання, чому формули робимо не широкими?
Відповідь наступна: оскільки значна частина аудиторії сайту заходить з мобільних пристроїв, а для них важливо, щоб формули вміщалися на екрані та були читабельними, то їх мінімізуємо по ширині де це є можливо.
Приклад 3.4 Визначити похідну dy/dx неявної функції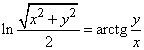
Обчислення: За методикою переносимо все в одну сторону від знаку рівності, пригадуємо похідну логарифма (13) та арктангенса (22) і обчислюємо, при цьому не забуваємо що обидві функції є складеними (множимо на похідну аргументу за змінними)
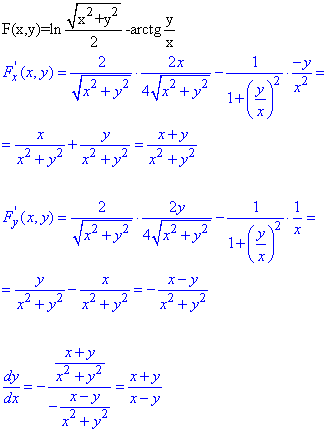
Друга похідна неявно заданої функції
Приклад 4.1 Обчислити другу похіднуy''
x2+2xy-y2=a2.
Обчислення: Першу похідну знаходимо за правилом для неявних функцій. Після того як ми маємо похідну в явному вигляді, то друга похідна неявної функції рівна похідній від обчисленої похідної. Нам не потрібно застосовувати правило для неявних ф-й двічі.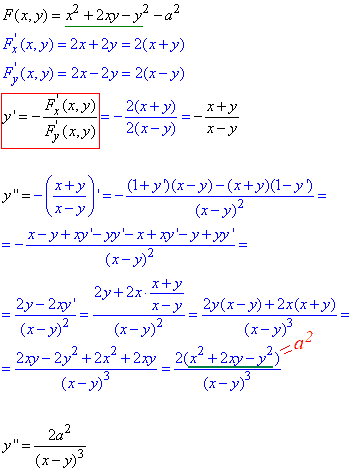
Вкінці розрахунків в чисельнику отримали вираз, що містить початково задану функцію, тому результат спростили.
Приклад 4.2 Знайти другу похідну y''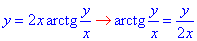 
Обчислення: Знову маємо неявно задану функцію, тому в умові зразу виконали певні перетворення, які при обчисленнях зведуть неявну похідну до компактного запису. Далі другу похідну знаходимо як похідну похідної.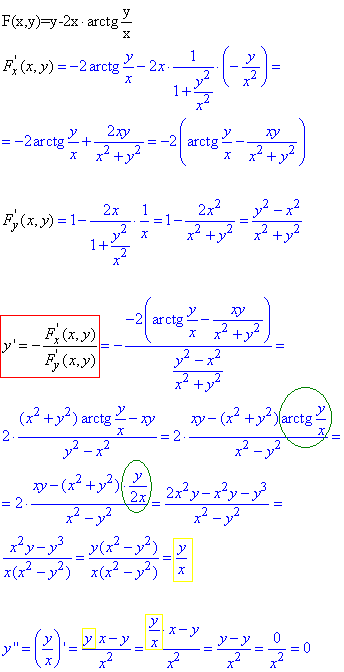
Попереду Вас чекають готові приклади на границі функцій багатьох змінних, пошук точок та характеру екстремуму, градієнту і ще багато чого з того, що Вас вчитимуть в курсі математичного аналізу.