Областю визначення називають множину значень аргументу x при яких існує значення y=f(x) і позначають D(y) або D(f).
Областю значень називають множину чисел, які приймає функція y=f(x) при проходженні аргументом x всіх визначених значень. Її позначають E(y) або E(f)..Графічно обидві множини добре ілюструє наступний рисунок
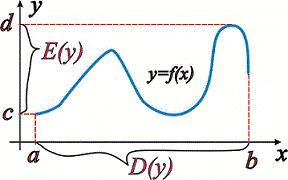
Для схематичної функції розглядувані області приймають значення
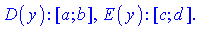
Методика знаходження області визначення для всіх функцій одна і та ж: потрібно виявити точки при яких функція не існує, а потім виключити їх з множини дійсних чисел R. В результати отримаємо набір проміжків чи інтервалів, точки, які і утворюють область визначення.
Особливості елементарних функцій
1) Якщо функція має вигляд полінома 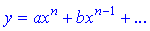 , то її областю визначення буде вся дійсна множина
, то її областю визначення буде вся дійсна множина 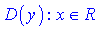 або
або 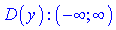 . Така функція визначена всюди.
. Така функція визначена всюди.
2) Дробово раціональна функція y=f(x)/g(x), де f(x),g(x) – поліноми областю визначення має всі значення аргумента при яких знаменник g(x) не перетворюється в нуль. Тобто розв'язуємо рівняння g(x)=0 і розв'язки, якщо ті існують, вирізаємо з множини дійсних значень. В результаті отримаємо набір інтервалів
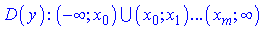
де x0,...,xm – корені рівняння g(x)=0.
3) Функція містить корінь парного степеня 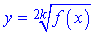 . В такому випадку областю визначення будуть точки x, при якому підкоренева функція приймає невід'ємні значення, тобто розв'язки нерівності f(x)>=0.
. В такому випадку областю визначення будуть точки x, при якому підкоренева функція приймає невід'ємні значення, тобто розв'язки нерівності f(x)>=0.
4) Якщо корінь міститься в знаменнику
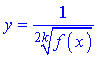
то область визначення визначаємо із строгої нерівності f(x)>0.
5) Якщо в знаменнику маємо корінь непарної степені
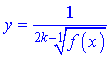
то область визначення знаходимо з умови, що функція не рівна нулеві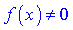 .
.
6) Якщо y(x) є логарифмом від іншої функції y=ln(f(x)), то за властивістю логарифма область визначення знаходимо з нерівності f(x)>0. Як правило, це буде інтервал або декілька інтервалів.
7) Експонента y=ef(x) областю визначення має значення x для яких визначена f(x). Для прикладу, функція y=ek*x визначена на всій дійсній осі.
8) Прості тригонометричні функції (косинус y=cos(x) та синус y=sin(x) визначені на всій множині дійсних чисел 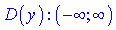 .
.
9) Тангенси y=tan(x) та котангенси y=cotan(x) областями визначення мають інтервали, які межують точками
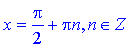
для першої функції та
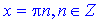
для другої, тобто
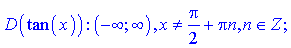
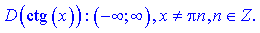
У випадках коли при аргументах є множники y=tan(k*x), точки в яких функція не існує слід визначати з умови
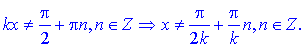
Подібним чином і для котангенса y=cotan(k*x)
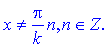
10) Варто зазначити, що обернені тригонометричні функції - арксинус y=arcsin(f(x)) і арккосинус y=arccos(f(x))областями значень мають відрізок [-1; 1]. Для відшукання їх областей визначення необхідно розв'язати подвійну нерівність 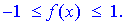
Наприклад, для функції y=arcsin(x+7) маємо нерівність 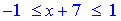 з якої отримаємо
з якої отримаємо 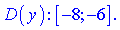
При суперпозиції функцій, тобто коли маємо їх комбінацію, потрібно знаходити область визначення кожної з функцій, після чого перетин знайдених областей.
Приклад 1 Знайти область визначення функції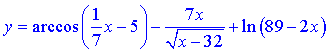
Розв'язання. Область визначення першого доданку знаходимо з нерівності
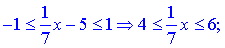
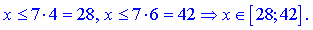
Дробова фунція з оренем у знаменнику та логарифм дадуть наступний вклад
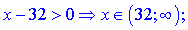
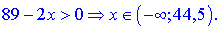
Перетином знайдених множин буде інтервал
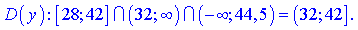
Це і є шукана область визначення.
Побудуємо графік функції в математичному пакеті Maple:
restart;
plot(arccos(x/7-5)-7*x/sqrt(x-32)+ln(89-2*x),x=30..44,-500..0);
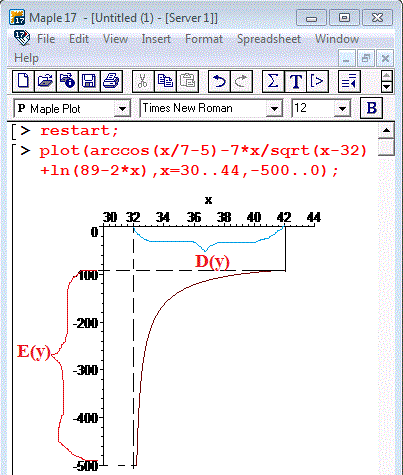
Аналогічним чином виконуть дослідження для функцій двох та більше змінних.
Приклад 2. Знайти і зобразити на малюнку область визначення функції двох змінних z=f(x,y).
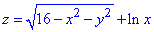
Обчислення: Випишемо ОДЗ кореневої функції та логарифма:
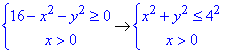
Це і є ті обмеження, які дозволяють побудувати область визначення.
На графіку отримаємо правий півкруг з центром у точці (0;0) і радіусом r=4.
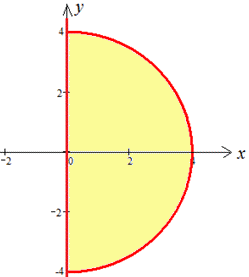
Знаходьте області визначення за наведеною схемою, виключайте всі зайві проміжки та точки та не допускайте помилок. Пам'ятайте, що встановлення областей визначення - це одне з найпростіших завдань при дослідженні функції.


