Запишемо правила знаходження похідних
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6) 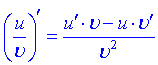
Тут С – стала величина (константа), ![]() – функції від аргументу x, що мають похідні.
– функції від аргументу x, що мають похідні.
7) Якщо маємо![]() – складену функція, тобто y=f(u), а u в свою чергу фунція від аргументу
– складену функція, тобто y=f(u), а u в свою чергу фунція від аргументу![]() , та існують окремо похідні обидвох функцій
, та існують окремо похідні обидвох функцій ![]() і
і ![]() , то існує похідна від y по x, причому
, то існує похідна від y по x, причому
![]()
Використовуючи наведене правило похідної складеної функції, таблицю похідних запишемо так
8) 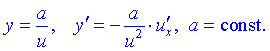
9) ![]()
10) 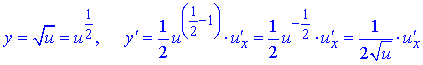
11) ![]()
12) ![]()
13) 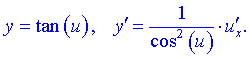
14) 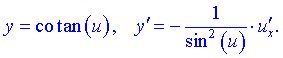
15) 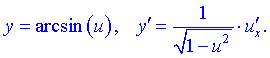
16) 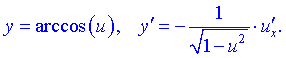
17) 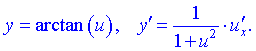
18) 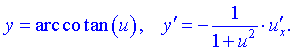
19) ![]()
20) ![]()
21) 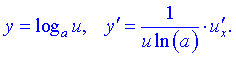
22) 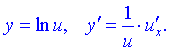
23) ![]()
![]()
В наступних статтях будуть показані правила диференціювання, враховуючи наведену таблицю похідних.
Якщо наведених формул похідних Вам мало (потрібні еліптичні чи інші спеціальні функції), то можете знайти онлайн в інтернеті та завантажити довідник з "формулами диференціювання" та теоремами, які застосовують при знаходженні похідних.

Приклад 1. Обчислити похідні функцій
1) ![]()
Розв'язок. За формулами диференціювання (1), (3), (8) знаходимо похідну полінома
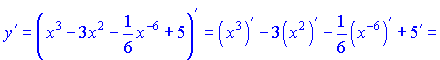
![]()
Похідна від сталої рівна нулю. Це правило найлегше, тому запам'ятайте його в числі перших.
2) 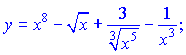
Розв'язок. Вводимо дробові та від'ємні степені, та перетворюємо задану функцію до вигляду
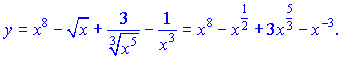
Використовуючи формули (3), (4), (7), знаходимо похідні
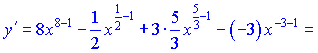
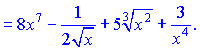
Вкінці записуємо результат через корені в знайдених степенях.
3) 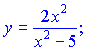
Розв'язок. Похідну дробової функції знаходимо за правилом похідної частки (6):
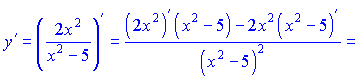
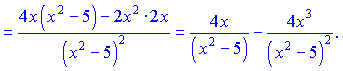
Обчислення не складні – в результаті диференціювання отримаємо різницю простих дробів 1 та 2 типу.
4) ![]()
Розв'язок. Похідну кореневої залежності ![]() шукаємо за правилом для складної функції
шукаємо за правилом для складної функції
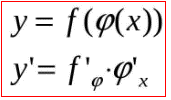
Тому вираз під коренем приймаємо за нову змінну φ=3+x5, беремо похідну від кореня по φта множимо на похідну від φ=3+x5 по "іксу":
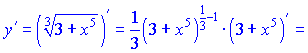
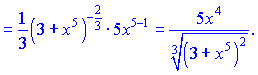
При роботі з дробовими показниками будьте уважні!
5) ![]()
Розв'язок. Похідну від добутку кореня на поліном знаходимо за правилом добутку функцій (5) та формулою похідної від складної функції. В результаті отримаємо наступні перетворення
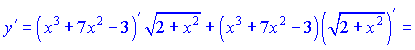
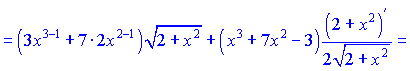
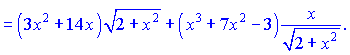
Записів багатенько, проте на практиці буде не легше, тож вивчайте правили диференціювання.
6) y=2sin(2x^3)
Розв'язок. За формулою похідної від складної функції отримаємо
![]()
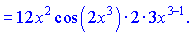
Останній вираз можете спростити, підсумувавши показники змінної.
7)y=(3x3-5x2+6)2
Розв'язок. Багато студентів, які ще добре не знають правил, спочатку підносять до квадрату вираз в дужках, а потім проводять диференціювання. Це неправильно, довго і важко. Скориставшись правилом диференціювання складної функції, отримаємо похідну від квадрата помножену на похідну кубічної функції
![]()
![]()
![]()
Якщо Ви будете підносити до квадрату, а потім диференціювати то отримаєте многочлен, який ще треба буде зводити до компактного вигляду. Результат буде правильний, але навіщо йти складним шляхом, якщо за нас вже давно придумали правила диференціювання, які спрощують обчислення. Вивчайте їх та користуйтеся на практиці.
Приклад 2 Знайти похідну першого порядку
y=5x^3-x^2+6x-4.
Розв'язування: За правилом похідної суми маємо
y'=(5x3-x2+6x-4)'=(5x3)'-(x2)'+(6x)'-(4)'=
=5·3x2-2x+6=15x2-2x+6.
Хто не розуміє чому так, рекомендуємо переглянути формули (1-8) крім (5-7), якщо далі не знаєте чому так вийшло - перегляньте попередні уроки.
Приклад 3 Знайти похідну функції
y=tg(7x+x^2).
Розв'язування: Під косинусом маємо не сам аргумент "x" як у формулі (16), а вираз 3x+1.
Щоб знайти похідну перепозначимо:
u=7x+x2, y=tg(u).
Тоді за правилом похідної складеної функції
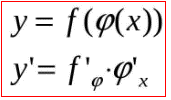
диференціюємо задану функцію
y'=(tg(u))'·u'x =1/cos2(u)·(7x+x2)'=
=(2x+7)/cos2(7x+x2).
Приклад 4 Знайти похідну
y=cos(3x+1).
Розв'язування: Алгортм обчислення похідної ідентичний до попереднього прикладу, тому на ньому зупинятися не будемо.
Краще уважно розберіть формулу
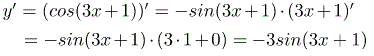
Думаю, що під силу знайти усім.
А щоб краще засвоїти матеріал, потрібно кілька завдань обчислити самостійно:
y=у3x-1;
y=√(2x+5);
y=sin(x2-2x-8);
y=ln(2x+7)·(3x2-5x+6);
y=√x/(x5+4x3+2).
В наступних уроках проаналізуємо ще більше готових похідних та пояснень як їх знайти в мат. пакетах та на онлайн сервісах.
]]>
Її завжди слід мати видрукованою під рукою і користуватися при обчисленнях як шпаргалкою. Голова не смітник, і всього що вчать не запам'ятати, а от вміти користуватися формулами та правильно знаходити похідні може навчитися кожен школяр і студент. Перші дві формули прості, перша говорить, що похідна від сталої рівна 0, друга - похідна "ікса" рівна одиниці.
Далі йдуть формули похідних суми, добутку та частки, їх застосовують коли задану функцію можна подати у вигляді суми, добутку чи частки функцій.
Окремий урок ми приділимо похідній складеної функції (24), а поки що ознайомтеся з формулою як її знаходити
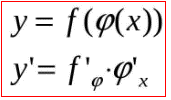
Далі на поширених з практичних прикладах навчимо Вас користуватися усіма приведеними тут формулами. Наостанок покажемо Вам, як можна знаходити похідні функцій в математичному пакеті Maple.
Похідна суми, добутку та частки функцій
Приклад 1 Знайдіть похідну
y=x5-4x3+2x2-7x.
Розв'язування: Використовуємо 2 та 8 формули та правила 3,4
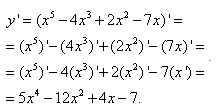
Отримали похідну
y'=5x4-12x2+4x-7.
Приклад 2 Обчисліть похідну
y=√(3x).
Розв'язування: Тут напряму формулу (9) не використаємо. Але можемо звести під формулу складеної функції.
Якщо y=f(u(x)), то похідна рівна y=f'u*u'x.
Для кореневої функції y=√(3x) виконаємо заміну:
u=3x, тоді y=√u.
Тоді за формулою (9) похідна рівна
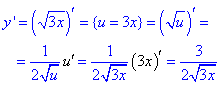
Приклад 3 Обчисліть похідну
y=53x+72x.
Розв'язування: Застосуємо десяту формулу для обчислення похідної показникової функції, тільки пам'ятаємо, що в степені не 1-ці, тому додатково домножуємо на похідну степеня (3x)'=3, (2x)'=2.
y'=(5^3x+7^2x)'= 53x·ln5·(3x)'+72x·ln7·(2x)'=
=3·53x·ln5+2·72x·ln7.
Спершу важко читати та зрозуміти як знаходили похідну, але вивчивши формули та правила, все стає зрозумілим.
Приклад 4 Обчисліть похідну
y=xa-b+x3.
Розв'язування: Вважаємо, що a-b≠0. Тоді похідну степеневої функції обчислюємо за формулою (8).
y'=(x^(a-b))'+(x3)'=(a-b)·xa-b-1+3x(3-1)=
=(a-b)·x(a-b-1)+3x2.
Формула похідної степеневої функції (xn)'=n·xn-1найпоширеніша на практиці, тому її добре запам'ятайте. Багато похідних складених або складних функцій обчислюють з її допомогою.
Якщо не вірите, прочитайте готові відповіді до наступних завдань.
Приклад 5 Знайдіть похідну функції
y=(x2-2x+3)5.
Розв'язування: На практиці ніхто з Вас не буде піднімати квадратний тричлен x2-2x+3 до 5 степеня, а тоді обчислювати похідну. За формулою складеної функції, перепозначимо:
y=u5, u=x2-2x+3.
Тоді похідна рівна
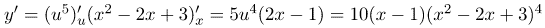
Простіше вже бути не може.
Приклад 6 Знайдіть похідну функції
y=sin3(x).
Розв'язування:Щоб були зрозіміліші пояснення до обчислення похідної, покладемо: u=sin(x),
тоді y=u3, а похідна рівна
y'=3u2·u'.
В результаті отримаємо
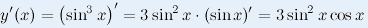
Приклад 7 Обчислити похідну
y=e3x+ex2+3x.
Розв'язування: Завдання на застосування похідної від експоненціальної функції (11). Тільки незрозуміло спершу, що робити з показником в другій експоненті x2+3x. Відповідь проста, перепозначити і знаходити за формулою похідної складеної функції.
u=3x, t=x2+3x, y=eu+et.
Тоді похідна суми експонент рівна
y'=(eu)'+(et)'=eu·u'+et·t'=
=e3x·(3x)'+ex2+3x·(x2+3x)'=
=3e3x+(x2+3x)·ex2+3x.
І так для всієї таблиці похідних, як тільки множник при "ікс" не рівний одиниці перепозначайте його і знаходьте похідну складеної функції, з часом Ви автоматично навчитеся записувати похідні без перепозначень.
Для прикладу
(e7x)'=e7x·7,
(e√x)'=e√x·(√x)'=e√x/(2√x),
(e3^x)=e3^x·(3x)'=3x·ln3·e3^x.
В такий спосіб можна поєднувати всі формули таблиці, але це в теорії, щоб навчити Вас аналітично обчислювати похідні. На практиці часто функції мають складний вигляд і усі обчислення похідних зводяться до приростів, градієнтів і т.д., які знаходять числово.
Приклад 8 Знайдіть похідну
y=e5sin(x)+cos(x)+2
Розв'язування: Можна вираз, що є в показнику експоненти позначити за нову змінну і далі похідну від експоненти по цій змінній помножити на похідну самої змінної.
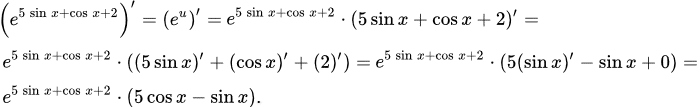
В попередніх завданнях ми вже ознайомилися з правилом похідної суми. Перейдемо до вивчення правила похідної добутку функцій
y'=(u·v)'=u'·v+u·v' (5)
Приклад 9 Знайти похідну за правилом добутку функцій
y=(1-x3)·(x4+4x).
Розв'язування: На початках для простоти обчислень, можете виконувати заміни:
u=1-x3, v=x4+4x, тоді y=u·v.
Далі за формулою похідної добутку функцій
y'=(u·v)'=u'·v+u·v',
обчислити похідні та підставити в праву сторону.
Спробуйте виконати так для кількох добутків функцій і Ви навчитеся обходитися без покрокового обчислення. Тоді Ваша відповідь прийде до наступного вигляду
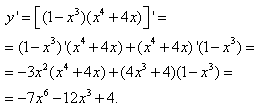
Спершу це важко зробити без помилок, але ми для того і вчимося, щоб вміти робити те, про що раніше не знали.
Приклад 10 Обчислити похідну функції
y=x2·ln(x+5).
Розв'язування: Застосуємо правило похідної добутку та формулу для логарифма (13). Перед переглядом відповіді можете самостійно знайти похідну, поклавши
y=u·v, u=x2, v=ln(x+5) в формулу (5).
Звірте чи отримали ту ж відповідь.
y'=(u·v)'=u'·v+u·v'
y'=(x2)'·ln(x+5)+x2·(ln(x+5))'=
=2x·ln(x+5)+x2·1/(x+5)·(x+5)'=
=2x·ln(x+5)+x2/(x+5).
З формули слідує, що якщо при аргументу "x" немає множника, а лише стала як доданок, то похідну можна не брати, тобто
(x+5)'=1,
а одиниця як множник "погоди" в похідну не вносить.
Познайомимося на кількох прикладах з формулою похідної частки функцій
y'=(u/v)'=(u'·v-u·v')/v2 (11)
Приклад 11 Обчислити похідну функції
y=(1+x2)/(1-x2).
Розв'язування: За правилом похідної частки в чисельнику дістанемо
(1+x2)*(1-x2)'+(1+x2)'*(1-x2),
в знаменнику похідної буде квадрат знаменника заданої функції.
Після розписання похідних та групування подібних доданків, остаточно отримаємо:
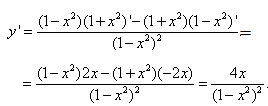
І так для всіх часток функцій, що Вам зустрічаються.
Приклад 12 Обчислити похідну функції
y=cos(x)/(x2+2x+3).
Розв'язування: Правило похідної частки дає наступний алгоритм обчислень.
В чисельнику похідної отримаємо
cos(x)*(x2+2x+3)'+(cos(x))'*(x2+2x+3),
в знаменнику квадрат знаменника, що заданий.
Знаходимо похідні та розписуємо
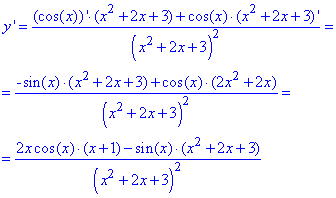
Винятком з правила частки є функції, де знаменник дробу можна загнати в чисельник як вираз з від'ємним степенем. Але це для простих функцій, тоді вдається розписати похідну за правилом добутку функцій.
Обчислення похідної в Maple
Далі навчимо Вас обчислювати похідні в математичному пакеті Maple. Його код простий для вивчення і в ньому легко досліджувати функції, знаходити інтеграли та похідні функцій, будувати графіки та обчислювати границі функцій.
Для обчислення похідної в Мейпл відповідає команда diff().
Приклад 13 Обчислити похідну
y=ex·(sin(x)-cos(x)).
Розв'язування: Застосуємо правило похідної добутку та формулу для логарифма 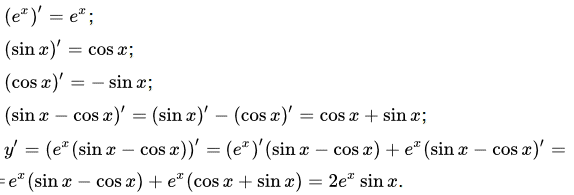
Перевіримо правильність обчислень в Мейплі. Для цього вводимо:
restart;
y := exp(x)*(sin(x)-cos(x));
DY := diff(y, x);
simplify(DY);
В результаті отримаємо
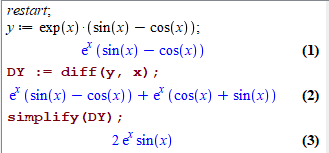
Тут довелося застосувати команду simplify(), для групування доданків після застосування правила множення.
Перевагою програмного знаходження похідних є те, що Ви не помилитеся з відповіддю, якщо правильно введете функцію.
Як перевірити похідну складеної функції?
Нехай маємо такі завдання.
Похідну наступних складених функцій будемо обчислювати за правилом
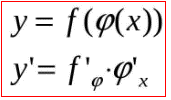
і для всіх вложених функцій.
Приклад 14 Знайти похідну функції
y=sin·(tg(√x)).
Розв'язування: Маємо косинус від тангенса від кореня квадратного. За правилом похідної складеної функції необхідно похідну від синуса (14) помножити на похідну від тангенса (16) по його внутрішній функції (по √x, не плутати з x) і помножити на похідну від кореня квадратного (9) по аргументу.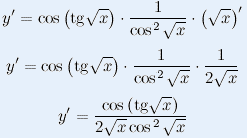
Повірте, що мало хто з Вас спершу отримає правильну відповідь.
Перевіримо похідну в Мейпл, поміняємо тільки перший рядок з попереднього прикладу, де замінимо функцію для диференціювання:
y := sin(tan(sqrt(x)));
DY := diff(y, x);
В результаті отримаємо
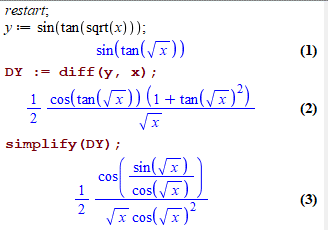
Легко догадатися, що в чисельнику в косинусі маємо формулу тангенса.
один в один як в аналітичному розв'язку.
Приклад 15 Знайти похідну функції
y=sin·(√(ln8x)).
Розв'язування: Маємо 3 вложені функції: корінь квадратний, логарифм та показникову 8x функції.
Щоб правильно знайти похідну приймайте внутрішню функцію за змінну, тоді зовнішні похідні знаходимо з таблиці, і кожен раз домножуємо на похідну від змінної по її "аргументу".
В такий спосіб дістанемо добуток похідних від синуса на похідну від кореня на похідну від логарифма і наостанок, це все множимо на похідну від 8x.
Кожен блок м виділили, щоб Вам простіше було читати формулу.
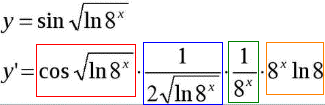
На 8x можна спростити, але це вже дрібниці в порівнянні з тим, що знайдено.
Перевіримо результат в мейплі.
y := sin(sqrt(ln(8x)));
DY := diff(y, x);
Результат знаходження похідної в Maple
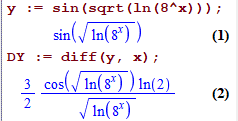
Як з ln(8) отримати ln(2) подумайте самостійно, тоді й переконаєтесь, що обидві відповіді співпадають.
На похдній добутку та частки функцій разом з Вами детальніше зупинимося в наступних уроках, також окремо розберемо похідні всіх можливих тригонометричних та обернених до них функцій. Практикуючи самостійно Ви поступово відшліфуєте формули, що тут даються і з часом, маючи під рукою саму лише таблицю похідних, зможете легко продиференціювати будь-яку складну функцію.
]]>По можливості майте таблицю похідних під рукою при вивченні теми диференціювання функцій та знаходженні похідних.

Правило похідної добутку функцій
y'=(u·v)'=u'·v+u·v' (5)
Приклад 1 Обчислити похідну
y=(3x+7)(2x3+4x+5).
Розв'язування: Багато студентів відкривають дужки і перемножають виразм в них, а вже тоді беруть похідну. Правильно в таких випадках використовувати формулу (5). Першу дужки позначимо за u, другу через v, та продиференціюємо
u'=(3x+7)'=3;
v'=(2x3+4x+5)'=6x2+4.
Можемо знайти похідну
y'=u'·v+u·v'=3(2x3+4x+5)+(3x+7)(6x2+4)=
=6x3+12x+15+18x3+42x2+12x+28=
=24x3+42x2+24x+43.
Тут в поясненнях правило похідної добутку містить лише перший рядок формули, решта все – це розкриття дужок та сумування подібних доданків.
Приклад 2 Обчислити похідну
y=x2sin(x).
Розв'язування: Проаналізуйте хід обчислення похідної за формулою:
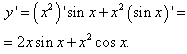
Приклад 3 Обчислити першу похідну
y=e2x·cos(6x-1).
Розв'язування: Спершу детально розглянемо правило похідної добутку функцій, потрібно знайти похідну першої функції та помножити на другу та додати похідну другої помножену на першу функцію.
Позначимо за u=e2x, v=cos(6x-1) та обчислимо їх похідні:
u'=(e2x)'=e2x·(2x)'=2e2x,
v'=(cos(6x-1))'=-sin(6x-1)·(6x-1)'=-6·sin(6x-1).
Підставляємо в формулу похідної добутку функцій
y=u'·v+u·v'=2e2x·cos(6x-1)-6e2x·sin(6x-1).
Приклад 4 Знайти похідну
y=ex·tg(x).
Розв'язування: З алгоритму знаємо, що спершу слід вибрати функції
u=ex, v=tg(x).
Далі знайти їх похідні
u'=(ex)'=ex;
v'=(tg(x))'=1/cos2(x).
та підставити за правилом (5):
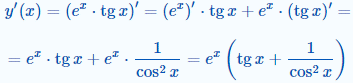
Проаналізуйте та спробуйте повторити самостійно.
Приклад 5 Знайти похідну
y=√x·(x2+3x+4).
Розв'язування: Завдання можна розв'язати без застосування правила добутку функцій. Для цього корінь квадратний подати як аргумент в степені 1/2 (x0.5), розкрити дужки і перемножити:
y=x0.5·(x2+3x+4)=x2+0.5+3x1+0.5+4x0.5.
Розпишіть самостійно, та застосуйте формули (8,9).
Ми ж вчимося використовувати похідну добутку:
y'=(√x)'·(x2+3x+4)+√x·(x2+3x+4)'=
=1/(2√x)·(x2+3x+4) +√x·(2x+3)=
=1/2·(x2+3x+4)·√x/x+·(2x+3)√x.
Можна ще згрупувати, але то вже робота для Вас.
Головне, що ми хотіли Вам донести, тут виконано.
Приклад 6 Знайти похідну
y=log2(3x+2)·ctg(5x).
Розв'язування: Обчислимо спершу похідну логарифма, котангенса та підставимо в формулу похідної добутку:
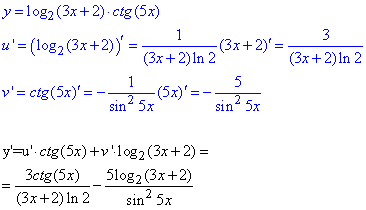
На попередньому уроці ми почали вивчати диференціювання фунцій в математичному пакеті Maple, сьогодні продовжимо на окремих прикладах.
Щоб продиференціювати задану функцію скористаємося кодом:
y1 := log[2](3*x+2)*cot(5*x);
DY := diff(y1, x);
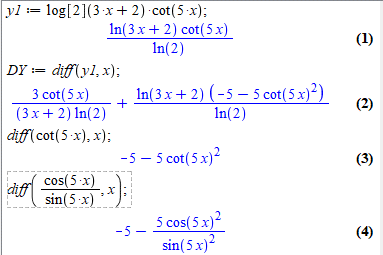
Результат в нас правильний, просто в Мейплі по своєму закладені формули окремих похідних.
Так, наприклад, похідна котангена рівна
(ctg(5x))'=5-ctg2(5x)
і при поданні котангенса через частку косинуса до синуса результат не зміниться, просто так закладено в програмі.
Приклад 7 Знайти похідну функції
y=e5x-1·sin2(x).
Розв'язування: Застосовуємо правило (5):
y'=(e5x-1)'·sin2(x)+e5x-1·(sin2(x))'=
=5e5x-1·sin2(x)+e5x-1·2sin(x)cos(x)=
=e5x-1·(5sin2(x)+sin(2x)).
Не бійтеся робити помилки та задавати "неправильні" питання, без цього неможливе будь-яке навчання.
Приклад 8 Обчислити похідну
y=√x·sin(x)·cos(x).
Розв'язування: Тут маємо добуток трьох функцій, але правило похідної добутку справедливе для будь-якої кількості ф-й.
В цьому прикладі добуток синуса на косинус можна замінити синусом подвійного кута, але ми не шукаємо легких шляхів, тому розбирайте відповідь нижче:
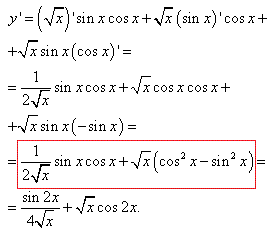
Перевіримо, яку похідну отримаємо в Maple
y1 := sqrt(x)*sin(x)*cos(x);
DY := diff(y1, x);
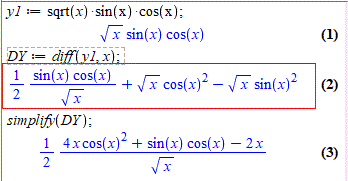
Похідна DY відповідає передостанньому рядку в наших обчисленнях, а от спрощення відрізняється, оскільки ми використали формулу косинуса подвійного кута.
На сайті wolframalpha похідна буде наступною:

Де краще та швидше вибирати Вам, але альтернативні варіанти знати потрібно.
Приклад 9 Знайти похідні функцій
а) y=(x+5)(x-8);
б) y=x2(2x-7);
в) y=√x(5-3x).
Розв'язування: Самостійно проаналізуйте готові похідні з формул:
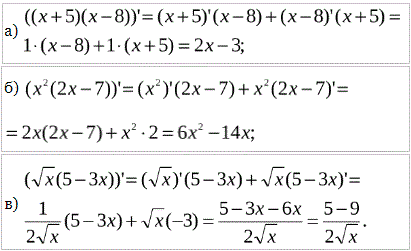
Приклад 10 Обчислити першу похідну
y=(2-x)/√2·arctg(x).
Розв'язування: Знайдемо похідну першої функції за правилом похідної частки (6):
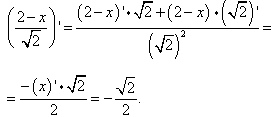
Можна було розписати дріб на сталу 2/√2 мінус "ікс" поділений на √2 та знайти похідну за правилом суми. Спробуйте цей варіант самостійно, це легший спосіб аніж запропонований.
Похідна від арктангенса за формулою (22) рівна
(arctg(x))'=1/(1+x2).
Підставляємо в правило похідної добутку:
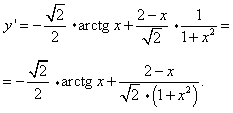
Вчіться на простіших завданнях, тому що на практичних прийдеться розбирати важчі приклади, а досвіду не будете мати як це правильно робити.
Правило похідної частки функцій
y'=(u/v)'=(u'·v-u·v')/v2 (6)
Повторно приводимо таблицю похідних, щоб мати їх перед очима при обчисленнях 
Приклад 1 Обчислити похідну
y=2/х.
Розв'язування: Застосовуємо правило похідної частки:
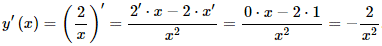
Можна було спростити розрахунки, враховуючи, що стала виносимо за похідну. Далі за формулою (7):
y=2·1/x;
y'=2*(1/x)'=2*(-1/x2)=-2/x2.
Приклад 2 Знайти похідну
y=(3x-1)/x4.
Розв'язування: За правилом (6) та формулами (2,8) розписуємо:
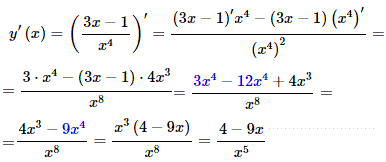
Коли в якості u, v задані поліноми чи експоненти, то, як правило, труднощів з обчисленнями немає.
Приклад 3 Знайти першу похідну
y=x/sin(x).
Розв'язування: Знаходимо похідну частки аргументу до синуса за формулою (6):
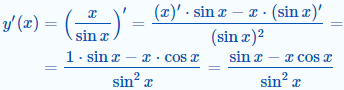
Приклад 4 Обчислити похідну функції
y=(x2+x+1)/(x2-x+1).
Розв'язування: Маємо частку поліномів. Можна окремо знайти похідні чисельника і знаменника та підставити в (6), або розписати як у формулі нижче:
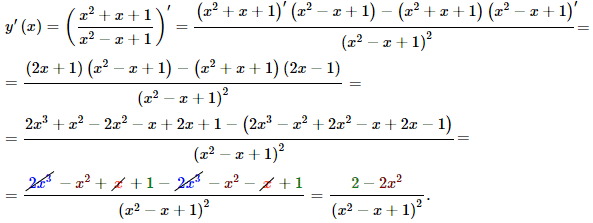
Перевіримо похідну функції в Мейплі
y1 := (x2+x+1)/(x2-x+1);
DY := diff(y1, x);
simplify(DY);
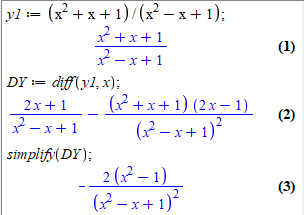
Результат порівняйте самостійно із раніше знайденим.
Приклад 5 Вивести першу похідну функції
y=(ax+b)/(cx+d).
Розв'язування: За правилом похідної частки функцій (6) отримаємо:
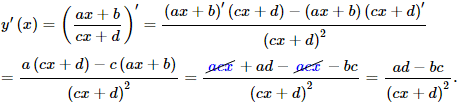
Приклад 6 Знайти похідну
y=(√x+1)/(√x-1).
Розв'язування: Похідні кореневих функцій обчислювали на попередньому уроці за формулою (9), тут додатково, ще використовуємо правило похідної частки функцій (6):
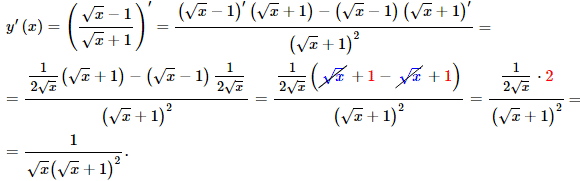
Приклад 7 Обчислити першу похідну
y=3/x-x/2+ln(x)/(2x).
Розв'язування: Застосовуємо правило похідної суми, та частки функцій до 1 та 3 доданку:
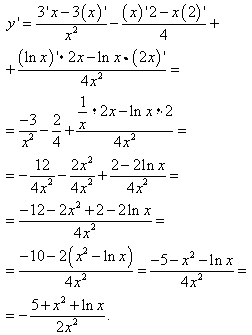
Перевіримо чи правильно знайшли похідну за допомогою Maple:
y1 := 3/x-(1/2)*x+ln(x)/(2*x);
DY := diff(y1, x);
simplify(DY);
В результаті отримаємо
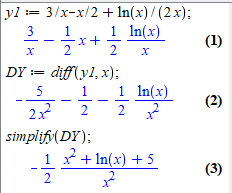
Порівнявши відповіді переконуємося, що похідна знайдена вірно.
Виконуємо розрахункові та контрольні з усіх тем, що є на сайті, тому сміло можете замовляти роботи або звертатися за консультацією щодо обчислень.
В наступних уроках розберемо нові функції та правила знаходження похідних від них, а покищо вправляйтеся самостійно.
]]>
В першу чергу Вам необхідно запам'ятати правила виділені червоними рамками - правило суми, похідна добутку та частки функцій, як брати похідну складеної функції.
Далі йдуть розв'язки завдань на похідні погруповані в блоки по 10 прикладів, не найпростіші з тих, що Вам доводилося бачити онлайн. Проте, на нашу думку, вони навчать Вас швидко користуватися таблицею похідних та будуть добрим довідником при розв'язуванні практичних в 11 класах та далі у ВУЗ-ах. Кому важко їх розбирати почніть з попередніх уроків, там дещо простіші приклади.
Приклад 1. В усіх завданнях необхідно знайти перші похідні. Пояснень не потрібно, все містять формули, дано мінімальний опис перед кожним блоком які правила застосовували. Перший блок прикладів на перші 8 формул таблиці похідних.
Завдання 1,2 на правило похідної суми (3), 3 завд. на формулу (24), 4 - на похідну добутку функцій, 5, 6, 8, 9, 10 - похідну складеної функції, 7- похідна степневої функції (8) коли степені від'ємні.
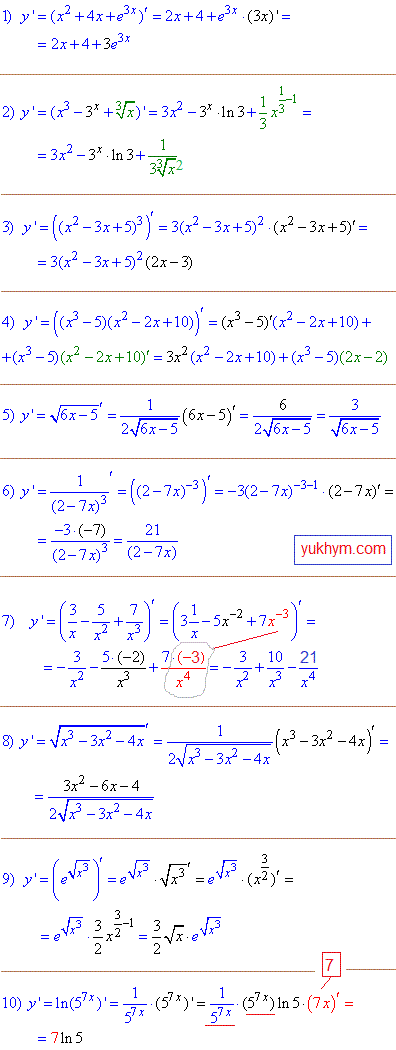
Приклад 2. В цьому блоці обчислюємо похідні на формули (10-13). Це експоненти, показникові функції та логарифми. Оскільки простіші приклади розібрані на попередніх уроках, то тут вчимося обчислювати похідні складених функцій. І щоб максимально наблизити до реалій практичних в багатьох завданнях вложеною функцією вибрано корінь квадратний, саме з ним в багатьох виникають труднощі на практичних та екзаменах.
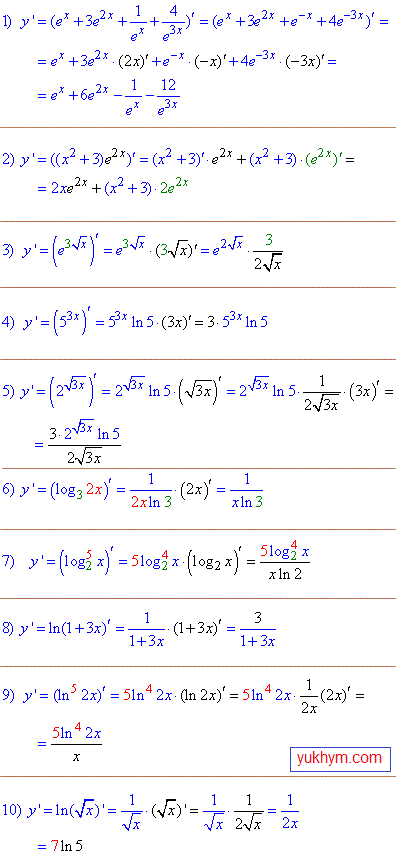
Приклад 3. Далі навчимося обчислювати похідні від тригонометричних функцій. Причому, аргументами в косинусах, синусах, тангенсах, котангенсах виступають складені функції. В більшості випадків лінійні (k·x), оскільки з ними найчастіше будете мати справу на практиці. Уважно розбирайте і запам'ятовуйте методику обчислення похідних.

Приклад 4. Окремої уваги заслуговують похідні обернених тригонометричних функцій. На екзаменах та практичних Ви повинні знати, як з допомогою формул (20-23) таблиці похідних обчислити аналогічні по складності завдання на арксинуси, арккосинуси. 7-10 завдання на похідні від арктангенса та арккотангенса, всюди складені похідні.
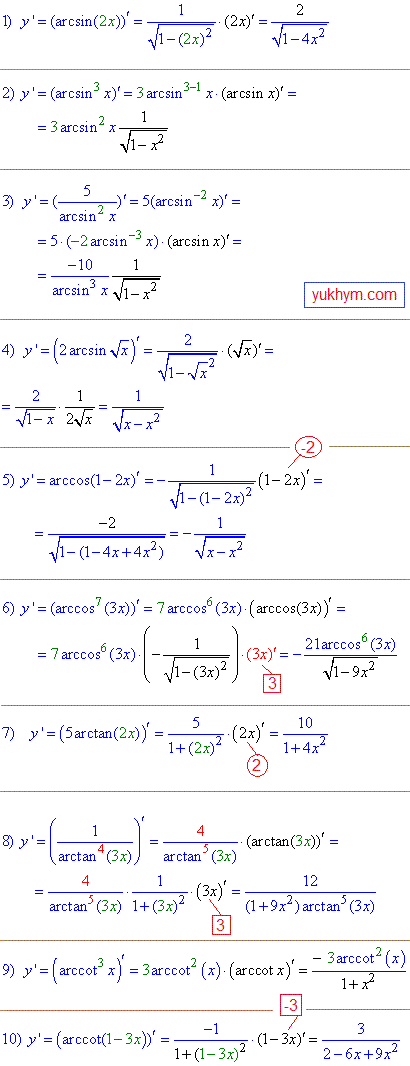
Приклад 5. В цьому блоці відібрано 10 готових відповідей на похідні добутку функцій. Поєднання добутків від коренів з синусами і експонент з логарифмами до степеневих та тригонометричних функцій.
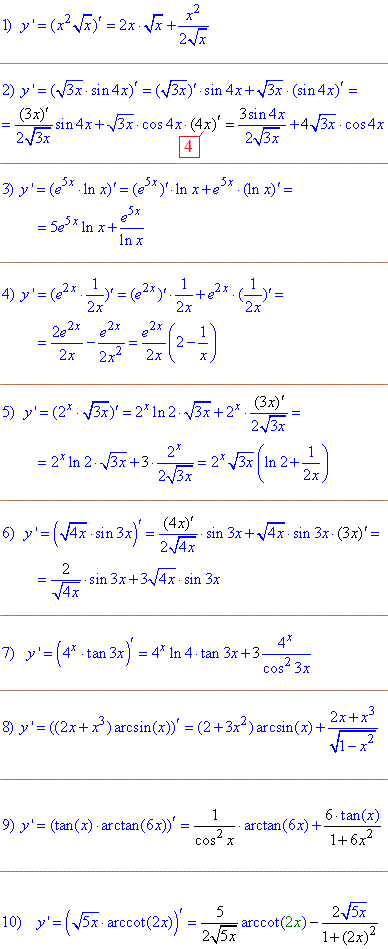
Пояснювати тут, що і для чого робили не будемо, все в наступній статті.
Окремо слід показати Вам чому рівні похідні гіперболічних та обернених гіперболічних функцій, але їх трохи багато, тому ми їх вирішили об'єднати та опублікувати новим уроком. Перед цим ще проаналізуємо з 20 прикладів на похідну добутку та частки функцій.

На сьогоднішньому уроці розберемо по 10 прикладів на похідну добутку функцій та 10 на частку функцій. Пояснень мінімум, але з формул все буде зрозуміло.
Формула похідної добутку функцій
y'=(u·v)'=u'·v+u·v' (5)
Інструкція до формул наступна: моменти, що важливі при обчисленні похідних виділені чорним кольором. Для економії місця в самих формулах не писали y'=, хоча всім зрозуміло, що їх шукаємо. Це для економії місця, оскільки понад 60% аудиторії сайту - це студенти і школярі, що заходять на сайт з мобільних пристроїв. Все для зручності їх навчання!
Приклад 1. Знайти похідні:
1) y=x2·√x.
Щоб продиференціювати добуток двох функцій похідну від першої функції множимо на 2 + добуток першої функції на похідну другої
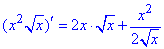
2) y=√(3x)·sin(4x).
Тут маємо добуток складених функцій, тому коли шукаємо похідну функції необхідно ще домножити на похідну вложеного аргументу!(k·x)'=k
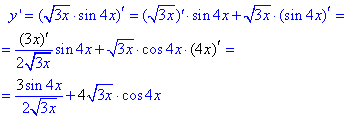
Обчислимо цю ж похідну, як на попередніх уроках, в мат. пакеті Maple:
y1 := sqrt(3*x)*sin(4*x);
diff(y1, x);
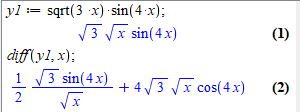
3) y=e5x·ln(x).
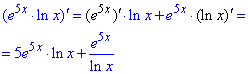
4) y=e2x·1/(2x).
Даний приклад можемо обчислювати як за формулою добутку, так і частки.
Основні похідні, що Ви маєте навчитися визначати виділені чорним.
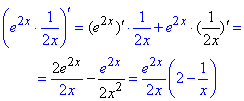
5) y=2x·√(3x).
За формулами (9, 10) знаходимо:
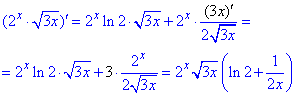
6) y=√(4x)·sin(3x).
Похідну кореня квадратного Ви бачили часто, похідна від синуса рівна косинусу + додатково скрізь домножуємо на похідну аргументу:
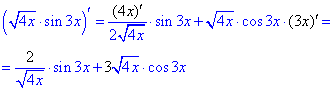
7) y=4x·tg(3x).
Тут при похідній тангенса дістанемо додатково 3 з похідної аргументу (3х)'=3.
Показникову функцію ми вже диференціювали не один раз і похідну Ви мали б знати як знайти.
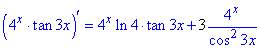
8) y=(2x+x3)·arcsin(x).
Похідна арксинуса в таблиці на початку уроку під 20 номером, поліноми за (3, 8) формулами.
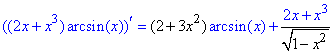
9) y=tg(x)·arctg(x).
Похідні тангенса та арктангенса це прості табличні формули (16, 22).
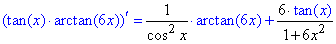
10) y=√(5x)·arcсtg(x).
Похідну арккотангенса знаходимо за формулою (23) таблиці:
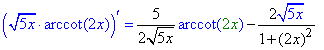
Все решта – просте правило похідної добутку.
Формула похідної частки функцій
y'=(u/v)'=(u'·v-u·v')/v2 (6)
Уважно проаналізуйте формулу, в чисельнику маємо вираз подібний до похідної добутку, тільки перед другим доданком знак мінус. В знаменнику квадрат знаменника заданої функції. Правило похідної частки легко і запам'ятати, і вивести з правила похідної добутку, замінивши ділення на функцію в знаменника на множення неї в -1 степені.
Переходимо до прикладів, по які Ви сюди й прийшли.
Приклад 2.Обчислити похідні:
11) y=(x2+3x-1)/(x3+4x).
Похідну частки поліномів рівна.
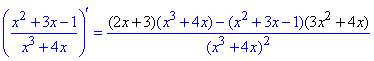
Щоб розписати розкрийте дужки в чисельнику та винесіть "ікс" із знаменника самостійно.
Ми ж знаємо як такі обчислення отримати в онлайн сервісі wolframalpha

12) y=arcсtg(x)/√(5x).
Коли беремо похідну від кореня, як складеної функції, то потрібно домножити на похідну від аргументу (5x)'=5.
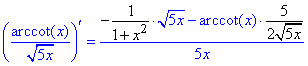
Щоб цього не робити можна √5 винести за дужки, тоді при похідній він залишиться в чисельнику
√5(√х)'=√5/(2√x).
Можна перевірити обчислення в Мейплі:
y1 := arccot(x)/sqrt(5*x);
DY := diff(y1, x);
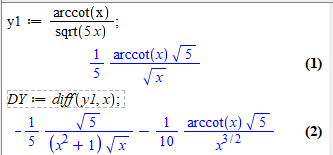
Можете перевірити самостійно та переконтися, що відповіді між собою рівні.
13) y=(x2-e5x)/(2x-x3).
Маємо поєднання показникових та степеневих функцій, уважно перегляньте як брати похідну.
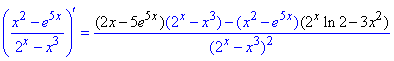
14) y=e3x/lg(2x).
lg - це логарифм десятковий, тому похідну знаходимо за формулою (12).
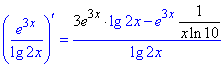
15) y=lg(5x)/3x.
Ще одне завдання на похідну логарифма десяткового, щоб Ви зауважили, що множник при "ікс" відсутній внаслідок спрощення від похідної складного аргументу.
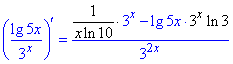
Це собі запам'ятайте або переглядайте ці приклади при підготовці до тестів чи екзаменів.
16) y=sin(x)/4x.
Такий розв'язок під силу усім, достатньо мати таблицю похідних.
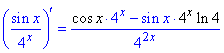
17) y=2x/tg(7-x).
Коли перед "іксом" знак мінус, то і похідна аргументу (7-x)'=-1, будьте уважні з цим. Решту обчислень диктує правило похідної частки функцій:
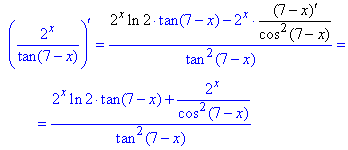
18) y=ln(x)/(x^2+7x).
Тут в чисельнику маємо табличний натуральний логарифм, в знаменнику поліном. За формулами (8, 13) знаходимо виділені далі похідні.
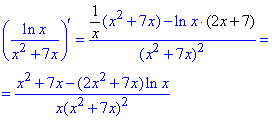
19) y=x1/3/e4x.
Похідну кореня кубічного, що є в чисельнику функції знаходимо за (8) формулою таблиці похідних. Похідна експоненти рівна самій експоненті + домножуємо на похідну аргументу (4x)'=4.
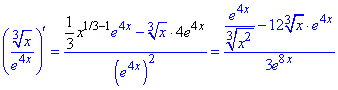
20) y=e3x/x2.
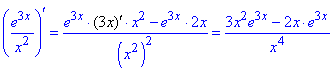
Сподіваюсь, що з цього уроку Ви взяли для себе багато нового. Вчіться використовувати формули похідних на практиці, все решта це просте групування подібних доданків та розкриття дужок.
Якщо виникають труднощі в розрахунках – звертайтесь за консультацією, можемо допомогти і з розв'язанням розрахункової чи підготовці до екзамену!
 Сьогодні навчимося знаходити похідні від функцій аргументом яких є функції від "ікс". Наприклад, щоб знайти похідну функції
Сьогодні навчимося знаходити похідні від функцій аргументом яких є функції від "ікс". Наприклад, щоб знайти похідну функціїy=(x3+x2+3x+7)5
подамо її у вигляді:
y=φ5, де φ=x3+x2+3x+7.
Тоді за формулою похідної складеної функції
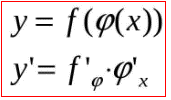 (1*)
(1*)отримаємо:
y'=(φ5)'·φ'x
За формулою 8
(φ5)'=5φ4,
φ'x=(x3+x2+3x+7)'=3x2+2x+3.
Підставляємо в y':
y'=5φ4·(3x2+2x+3)=5(x3+x2+3x+7)4·(3x2+2x+3).
Формулу (1*) використовуємо для всеможливих вкладених функцій.
Приклад 1 Обчислити похідну
y=(6-7x)10.
Розв'язування: Позначимо через φ вираз в дужках
y=φ10, φ=6-7x, φ'=-7.
Тоді за правилом похідної складної функції:
y'=(φ10)'·φ'=-7·10φ9=-70(6-7x)9.
Такі обчислення під силу виконати кожному. З досвідом Ви навчитеся знаходити похідну без позначення вкладених функцій.
Приклад 2 Обчислити похідну
y=ln(3x+7).
Розв'язування: Застосовуємо формулу для логарифма (13) та правило (1*):
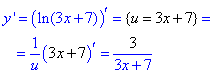
Приклад 3 Знайти похідну
y=e(x^2+4x).
Розв'язування: Показник експонетнти є функцією від "ікс", тому:
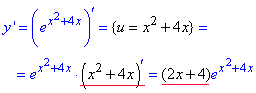
Приклад 4 Знайти першу похідну
y=√(x2+4x+3).
Розв'язування: Похідна кореня квадратного від квадратичної функції за формулами (1*,9) рівна:
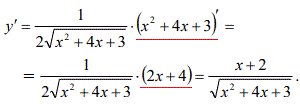
Приклад 5 Знайти похідну
y=sin(x3+5x2-1).
Розв'язування: Похідна від синуса рівна косинусу і за рахунок складеної функції домножуємо на похідну від полінома
y'=cos(x3+5x2-1)·(x3+5x2-1)'=
=(3x2+10x)cos(x3+5x2-1).
Приклад 6 Знайти похідну
y=cos5(x).
Розв'язування: Якщо задана будь-яка тригонометрична (чи будь-яка з таблиці похідних**) функція в певному степені, то за правилом похідної складеної функції за аргумент позначають саму тригонометричну (**) функцію.
y=u^5, u=cos(x).
Тоді маємо
y'=5u4·u'x=5u4·(cos(x))'=
=5cos4(x)·(-sin(x))=-5cos4(x)·sin(x).
Аналогічно похідні для тангенса та котангенса
y=tan3(x), (16)->
y'=3tan2(x)*(tan(x))'=3tan2(x)/cos2(x);
y=cot4(x), (17)->
y'=4ctg3(x)·(-1/sin2(x))=-4ctg3(x)/sin2(x).
Приклад 7 Знайти похідну
y=ctg(x4).
Розв'язування:В таких завданнях за вкладену функцію покладають
y=ctg(u), u=x4,
u'=4x3.
Обчислюємо похідну
y'=ctg(u)'·u'=-1/sin2(u)·4x3=
=-4x3/sin2(x4).
Приклад 8 Знайти похідну
y=sec2(3x).
Розв'язування: Похідну від секанса знаходимо за формулою (18)+ перед тим похідна степеневої функції
y'=2sec(3x)·(sec(3x))'=
=2sec(3x)·sec(3x)·tan(3x)*(3x)'=
=6sec2(3x)·sec(3x)·tan(3x).
Для перевірки виконаємо диференціювання в Maple:
y1 := sec(3*x)^2;
DY := diff(y1, x);
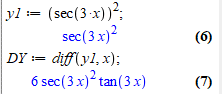
Швидко і просто.
Розглянемо кілька вложених функцій.
Приклад 9 Знайти похідну
y=tan(ln√3x).
Розв'язування: Для тангенса вкладеною функціює буде логарифм, для логарифма корінь, для кореня вкладеною ф-єю є 3х.
Тому за формулою (1*) маємо добуток похідної від тангенса на похідну від логарифма на похідну від кореня квадратного і на 3=(3х)':
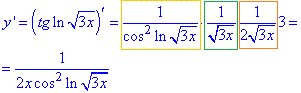
В мейплі похідна рівна:
diff(tan(ln(sqrt(3*x))),x)

В мат пакеті закладена формула переходу
1/cos2(x)=1+tg2(x).
Обчислимо ту ж похідну онлайн на wolframalpha:

Відповідь нас задовільняє.
Приклад 10 Обчислити y', якщо
y=√e2x-1.
Розв'язування: Рухаємося від кореня квадратного до експоненти далі до степеня:
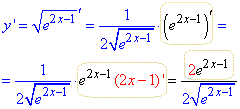
Розберемо ще завдання де маємо добуток та частку складених функцій
Приклад 11Знайти y', якщо:
y=ex^2·cos(ln(x)).
Розв'язування: За правилом похідної добутку функцій (5)
(u·v)'= похідну першої функції помножити на другу + похідну другої *на першу ф-ю.
Знайдемо спершу оремі похідні:
(ex^2)'=ex^2·(x2)'=2x·ex^2;
cos(ln(x))'=-sin(ln(x))·(ln(x))'=
= -sin(ln(x))/x.
Записуємо похідну:
y'=2x·ex^2·cos(ln(x))-ex^2·sin(ln(x))/x.
Знайдемо похідну в мат. пакеті Мейпл:
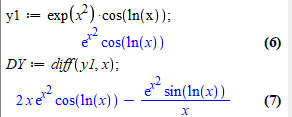
Приклад 12 Знайти похідну функції:
y=√ln(x)/etg(x).
Розв'язування: У формулі похідної частки двох функцій (6) фігурують похідні чисельника та знаменника, тому з їх обчислення і почнемо:
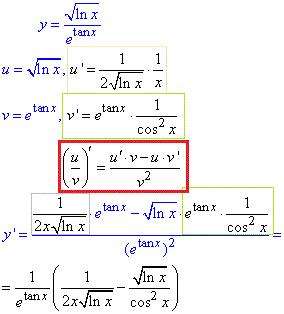
Паралельно проводимо розрахунки похідної в Maple та Wolframalpha:
y1 := sqrt(ln(x))/exp(tan(x));
DY := diff(y1, x);

З точністю до тригонометричних формул результати співпадають.
Далі вас чекають уроки на обчислення похідних неявно та параметрично заданих функцій, метод логарифмування та багато нового з диференціювання.
]]>В таких випадках доцільно обидві частини виразу спочатку прологарифмувати за експонентою (e), а потім приступити до диференціювання. Цей спосіб одержав назву логарифмічного диференціювання. Похідну від логарифма функції називають логарифмічною похідною. Суть методу за допомогою формул можна описати наступним чином:
маємо складну функцію вигляду y=t(x);
до обох сторін застосовуємо логарифмування
ln(y)=ln(t(x))
і знаходимо похідні правої і лівої частини рівності у вигляді формул
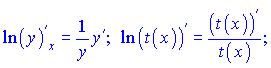
Прирівнюємо похідні і виражаємо y'
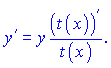
В цьому вся суть методу, далі все залежить від функції t(x).
Якщо t(x) задана добутком функцій
то за властивостями логарифма при диференціюванні отримаємо суму логарифмів
Якщо маємо дробову функцію
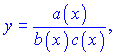
то, застосовуючи логарифмування, отримаємо різницю логарифмів
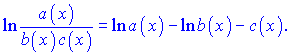
Якщо маємо складену показникову функцію (функція в степені іншої)
то за властивостями логарифма отримаємо залежність
У випадку коренів (g(x)=С=1/2; 1/3, ...) диференціювання значно спрощується і отриамємо добуток показника на огарифм
![]()
Подальше обчислення похідних залежить від складності самих функцій. Розглянемо конкретні завдання, щоб даний матеріал став для Вас більш зрозумілішим і наочнішим.
Приклад 1. Використовуючи логарифмування знайти похідну
(Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач" )
1) (5.2.178) y=x5x
Розв'язок. Приклади вибрано складні для того, щоб розкрити всю силу методу логарифмічного диференціювання та розглянути поширені для студентсьої практики приклади. Проведемо логарифмування лівої і правої частин
![]()
Далі знайдемо похідну добутку функцій
![]()
![]()
Похідна лівої частини показана при викладі теоретичного матеріалу. Записуємо результати обчислень
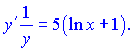
Далі переносимо функцію y із знаменника в праву частину та не забуваємо замінити її значення на вихідне
![]()
Незважаючи на складний вигляд даний приклад розв'язано.
2) (5.2.191)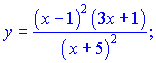
Розв'язок.Знаходимо логарифм дробової функції
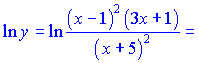
![]()
Проводимо диференціювання обох частин залежності
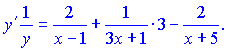
Зведемо під спільний знаменник праву сторону. В результаті математичних операцій отримаємо
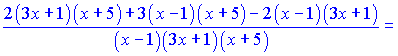
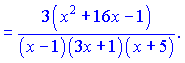
Підставимо в вихідну формулу, перенісши функцію в праву частину
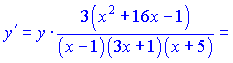
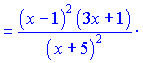
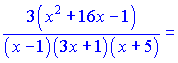
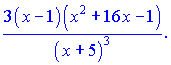
В результаті ряду нескладних маніпуляцій отримали досить компактний кінцевий результат похідної. При обчисленні даного прикладу напряму подібний результат довелося б шукати дуже довго.
3) (5.2.195)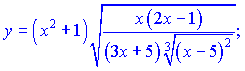
Розв'язок.Незважаючи на складний вигляд, дану функцію на основі властивостей поазників можна переписати у вигляді
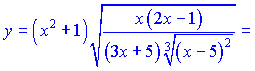
![]()
![]()
Застосуємо логарифмування
![]()
![]()
Похідна від правої частини рівна
![]()
![]()
![]()
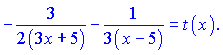
Тут для спрощення подальших викладок позначии резуьтат диференціювання через t(x).
Враховуючи похідну від ln(y), остаточно отримаємо
![]()
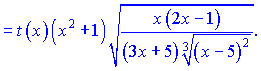
Можна залишати в такому вигляді, оскільки суть даного уроку навчитися застосовувати метод логарифмічного диференціювання. Проте, якщо Ви захочете для спрощення звести все до спільного знаменника, то отримаєте таку відповідь
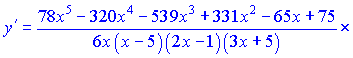
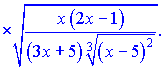
Повірте - це займе у Вас чимало часу
4) (5.2.199)![]()
Розв'язок.Проводимо логарифмування функції
![]()
![]()
Далі за наведеною схемою знаходимо диференціюємо праву частину залежності
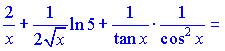
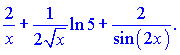
Підставивши в формулу для похідної від логарифма, отримаємо
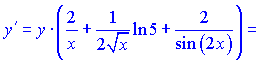
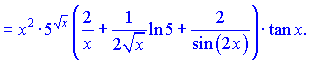
На цьому розв'язування прикладу завершено.
Практикуйте з подібними завданнями і через певний час у Вас не буде жодних труднощів із знаходженням похідної через огарифмування функції.
f(x,y)=0
з якої не можна відокремити саму функцію. В цьому випадку функція y(x) називається неявною функцією від аргумента x.
Однак саму похідну від функції по змінній x можна обчислити. Для цього диференціюють функцію f(x,y) по x, при цьому враховують, що сама функція залежна від змінної y=y(x). З одержаного рівняння згруповують доданки, що містяться при похідній y' і виражають її.
Як це виглядає на пракиці проілюстровано на прикладах із Дубовика В.П., Юрика І.І. "Вища математика. Збірник задач".
Приклад 1. Знайти похідні неявно від заданих функцій y(x) .
1) (5.219) 3x+3y=3x-y
Розв'язок:Продиференціюємо праву і ліву частини
![]()
![]()
Отриманий вираз поділимо на спільний множник ln(3) та згрупуємо доданки, що містять похідну y'(x) і перенесемо їх в одну сторону за знак рівності. В результаті отримаємо
![]()
Поділивши на множник при похідній y'(x) отримаємо її значення
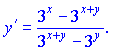
Для спрощення винесемо із чисельника та знаменника спільні множники 3x та 3y відповідно. В результаті отримаємо:
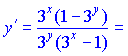
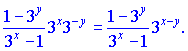
Як бачите, нічого складного ми не робили, проте швидко відшукали похідну неявно заданої функції. Розглянемо наступне завдання.
2) (5.223)![]()
Розв'язок:Проведемо диференціювання виразу. Перший доданок дасть 2, похідну від арккосинуса знаходимо за правилом складеної фунції
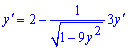
Виділяємо доданки, що містять похідну y'(x)
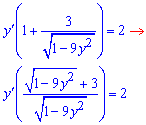
Поділимо на множник при похідній та відшукаємо її значення
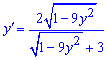
Завдання повністю розв'язане.
3) (5.227)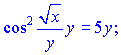
Розв'язок:Обчислимо похідну правої і лівої частини, від косинуса знаходимо, як від складеної функції
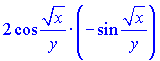
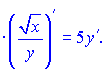
Похідну від частки функцій рівна
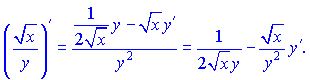
Перших два множники рівні синусу подвійного кута. Тому похідні можемо згрупувати у вигляді
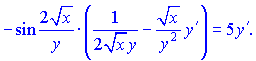
Домножимо праву та ліву частини на множник ![]() , щоб позбутися знаменників та згрупуємо доданки при похідній y'(x)
, щоб позбутися знаменників та згрупуємо доданки при похідній y'(x)
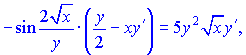
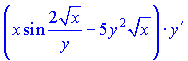
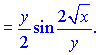
З останньої залежності знаходимо значення потрібної похідної
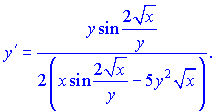
В такого роду прикладах головне не помилитися при відшуканні похідних. Фугкції тут взято доволі складні, заодно вивчете інші правила диференціювання.
4) (5.236)![]()
Розв'язок:Диференціюємо неявно задану функцію по змінній
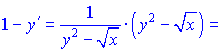
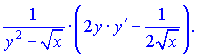
Перегрупуємо доданки, що містять y'
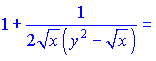
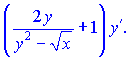
Зводимо вирази до спільного знаменника
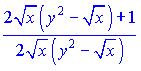
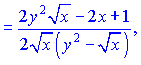
та підставляємо їх на свої місця
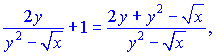
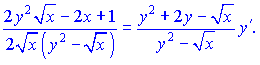
Звідси виражаємо похідну функції
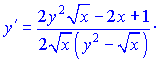
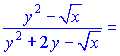
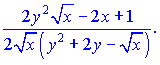
На цьому завдання розв'язано.
При обчисленні похідної неявно заданої функції типовими помилками на практиці є неправильне взяття похідної та плутанина зі знаками при групуванні подібних доданків. Будьте уважні в таких ситуаціях та не допускайте помилок. На скадних умовах Ви побачили як брати похідну від неявно заданої функцій, тому, якщо попрацюєте самостійно, то з даної теми отримаєте хороші результати на тастах, контрольних.
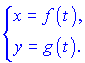
Похідна параметричної функції першого порядку знаходиться за правилом
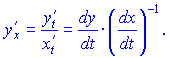
Друга похідна параметрично заданої функції визначається залежністю
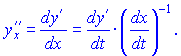
Аналогічним чином можна вивести похідні старших порядів.
Розглянемо декілька прикладів для закріплення матеріалу на практиці.
Приклад 1. Знайти похідні функцій , заданих параметрично.
(Дубовик В.П., Юрик І.І. "Вища математика. Збірник задач" )
1) (5.253) 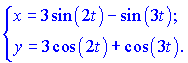
Розв'язок. Обчислимо похідні функції та аргументу за параметром t
![]()
![]()
![]()
Знайдені значення підставляємо у формулу похідної
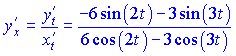
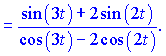
В даному випадку, щоб не виносити знак мінус перед дріб, домножили на (-1) знаменник та переставили доданки так, щоб першими йшли додатні. Сама ж крива на площині матиме вигляд
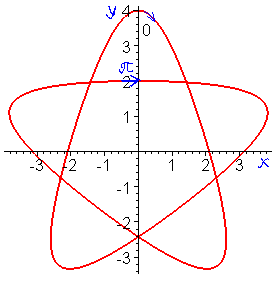
2) (5.256) 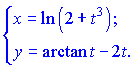
Розв'язок. Обчислюємо похідні x,y за параметром
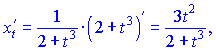
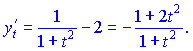
Обчислюємо значення похідної ![]()
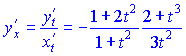
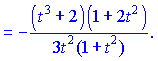
Приклад не складний, головне правильно знайти похідні логарифма та арктангенса.
3) (5.261) 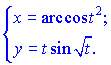
Розв'язок.Знходимо похідні сладених функцій
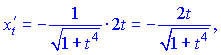
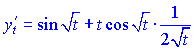
![]()
Отримані значення підставимо у формулу похідної параметричної функції ![]()
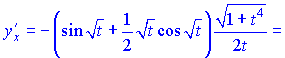
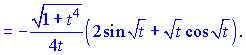
Головне у всіх прикладах не "наламати дров" при знаходженні похідних. Це найважча і відповідальна частина диференціювання параметрично заданих функцій.
4) (5.263) 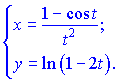
Розв'язок. Продиференціюємо функцію та аргумент за параметром t
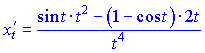
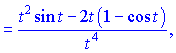
![]()
Отримані значення підставляємо у формулу і спрощуємо чисельник та знаменник на t
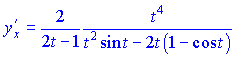
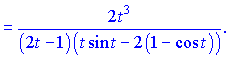
З прикладів бачимо, що обчислення похідної від параметрично заданої функції не надто складне. Дотримуйтеся послідовності виконання дій, будьте уважні при спрощенні виразів і все у Вас вийде правильно.