Целочисленная случайная величина X имеет биномиальное распределение, если вероятность ее возможных значений вычисляется по формуле Бернулли
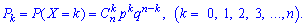
В табличной форме этот закон имеет следующий вид:
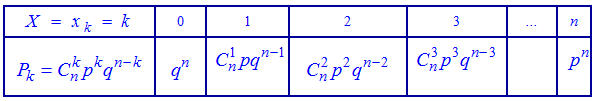
При проверке выполнения условия нормировки используется формула бинома Ньютона, поэтому закон распределения называют биномиальным
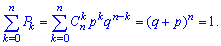
Построим вероятностную образующую функцию для этого закона
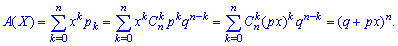
Итак, вероятностная образующая функция для биномиального закона ровна
Найдем основные числовые характеристики для этого закона
1. Математическое ожидание случайной величины через образующую функцию для биномиального распределения вычисляем по формуле
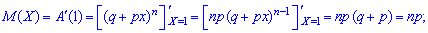
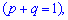
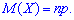
2. Вторая производная от образующей функции для биномиального распределения в единице примет значение
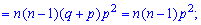
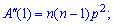
На основе найденного значения можно вычислять дисперсию
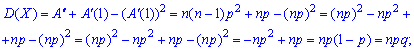
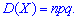
Имея дисперсию нетрудно установить среднее математическое отклонение
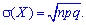
3. Коэффициент асимметрии А(Х) и эксцесс Е(Х) для биномиального распределения определяют по формулам
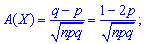
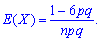
В случае роста количества испытаний n асимметрия и эксцесс стремятся к нулю.
Перейдем к практической стороне биномиального распределения
Задача 1. В партии однотипных деталей стандартные составляют 97%. Наугад из партии берут 400 деталей. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение М(Х), D(X), S(Х) для дискретной случайной величины Х — появления числа стандартных деталей среди 400 наугад взятых.
Решение. Целочисленных случайная величина Х имеет биномиальное закон распределения вероятностей, которая может принимать значения Х = k = 0, 1, 2, ..., 400. Вероятности возможных значений для данной задачи определяются по формуле Бернулли и составляют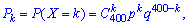 
где р = 0,97 — вероятность появления стандартной детали, q = 1 – p =1 – 0,97 = 0,03 — вероятность появления нестандартной детали. Согласно приведенным выше формулам определяем нужные величины:
------------------------------------
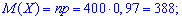
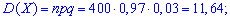
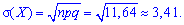
Задача 2. Два ювелирные заводы производят свадебные кольца в объеме 3:7. Первый завод производит 95% колец без дефекта, второй – 90%. Молодая пара перед свадьбой покупает пару колец. Построить закон распределения, вычислить математическое ожидание и среднее квадратичное отклонение.
Решение. Вероятность события А – куплена кольцо оказалась качественной определим по формуле полной вероятности
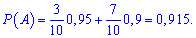
Случайная величина Х – количество колец надлежащего качества среди купленных имеет биномиальное закон распределения с параметрами
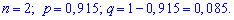
Найдем соответствующие вероятности
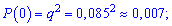
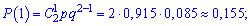
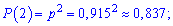
Запишем таблицу распределения
На основе табличных данных вычисляем математическое ожидание
дисперсию
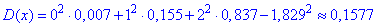
Среднее квадратичное отклонение
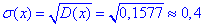
Как можно убедиться из примеров, биномиальний закон распределения простой как для понимания так и для вычислений. Хорошо разберитесь с примерами и пользуйтесь биномиальным распределением там где это необходимо.
