Под испытанием (экспериментом) понимают некоторую совокупность условий, при которых наблюдается то или иное явление, фиксируется тот или иной результат. Опыт может проводиться многократно в подобных (неизменных основных) условиях, однако ряд второстепенных условий и факторов, которые невозможно проконтролировать изменяется от испытания к испытанию и приводят к разным результатам последствий эксперимента.
Случайным событием (событием) называется любой факт, который в результате эксперимента может состояться или не состояться. Случайные события обозначают большими латинскими буквами 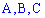 .
.
Вероятностью события называется численная мера свободы уверенности в появлении данного события вследствие нового испытания.
Вероятность события 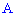 обозначается как
обозначается как 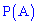 .
.
Вероятной (достоверностью) называется событие  , которое в результате испытания непременно должно произойти. Для достоверного события вероятность равна единице
, которое в результате испытания непременно должно произойти. Для достоверного события вероятность равна единице 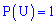 .
.
Невозможным называется такое событие  , которое в результате опыта не может произойти.
, которое в результате опыта не может произойти.
Для невозможного события вероятность равна нулю 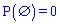 .
.
Вероятность любого случайного события 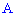 принимает значения между нулем и единицей:
принимает значения между нулем и единицей:
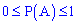 .
.
Полной группой событий называется ряд таких событий , что в результате испытания непременно должно произойти хотя бы одно из них. Несколько событий в опыте называются несовместимыми, если никакие два из них не могут появиться одновременно.
Несколько событий в испытании называются равновозможными, если они имеют равные шансы появления в результате испытания. Примерами равновозможных событий можно отметить появление: герба или цифры при одном подбрасывании монеты; четного и нечетного числа очков при одном подбрасывании игрального кубика и т.д.
Если последствия испытания образуют полную группу несовместных равновозможных событий, то они называются случаями.
Множество всех результатов эксперимента, которое рассматривается называется пространством элементарных событий.
Следствие (случай) называется благоприятным событию 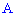 , если оно приводит к обязательному появлению события
, если оно приводит к обязательному появлению события 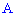 .
.
Классическое определения вероятности
Если результаты испытания сводятся к схеме случаев, то вероятность события 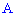 вычисляется по формуле
вычисляется по формуле
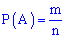
Где 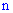 – общее число случаев;
– общее число случаев;  – число случаев, благоприятствующих событию
– число случаев, благоприятствующих событию 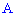 .
.
Приведенное соотношение является классической формулой вычисления вероятности событий.
----------------------------------------------
Приведем несколько типичных примеров.
Пример 1. В цеху по изготовлению мячей для гольфа в одной коробке было 67 мячей правильной формы и 23 мяча неправильной формы в другой. Мячи ссыпали в одну коробку. Какова вероятность того, что наугад извлечен мяч будет неправильной формы ?
Решение
Общее число равновозможных событий равна количеству всех мячей
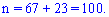
Число способствующих событий, которые заключается в извлечении бракованного мяча - равны их количеству
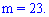
По формуле вычисляем
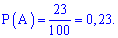
----------------------------------------------
Пример 2. На столе выложены кубики с номерами от единицы до девяти. Ученик наугад вытаскивает один кубик. Какова вероятность того, что:
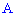 - число из кубика делится на 3?
- число из кубика делится на 3?
 - число делится на 2?
- число делится на 2?
Решение
Общее число случайных событий равно количеству кубиков
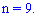
Число способствующих событию 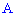 можно изобразить в виде множества
можно изобразить в виде множества 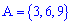 , для В множество благоприятных событий будет следующим
, для В множество благоприятных событий будет следующим 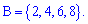 На основе этого число
На основе этого число  принимает значение
принимает значение 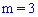 и
и 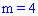 для первого и второго события соответственно. Вероятность их появления определяем по известной формуле
для первого и второго события соответственно. Вероятность их появления определяем по известной формуле
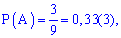
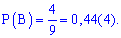
Пример 3. В группе 17 ребят и 13 девушек. Преподавателю нужно вызвать кого-то для проверки выполнения домашних заданий. Какова вероятность того, что к доске выйдет девушка?
Решение
Общее число равносильных событий равно количеству учащихся
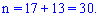
Число девушек равно 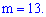
Тогда искомая вероятность
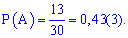
]]>
При большом числе возможных последствий испытания способы прямого перебора возможных вариантов малоэффективны. На помощь приходят комбинаторные методы, в основе которых лежат два следующих правила.
ПРАВИЛО СУММИРОВАНИЯ
Если два взаимоисключающие действия могут быть выполнены в соответствии 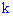 и
и  способами, тогда какое-то одно из этих действий можно выполнить
способами, тогда какое-то одно из этих действий можно выполнить 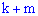 способами.
способами.
Пример 1. Из города А в город В можно добраться 12 поездами, 3 самолетами, 23 автобусами. Сколькими способами можно добраться из города А в город В?
Решение. Проезд из А в В на поезде, самолете или автобусе являются событиями, которые не могут выполняться одновременно одним человеком (взаимоисключающими), поэтому общее количество маршрутов можно вычислить суммированием способов передвижения
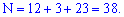
ПРАВИЛО ПРОИЗВЕДЕНИЯ
Пусть две выполняемые одно за другим действия могут быть осуществлены в соответствии 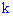 и
и  способами. Тогда обе они могут быть выполнены
способами. Тогда обе они могут быть выполнены 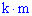 способами.
способами.
----------------------------
Пример 2. В турнире принимают участие 8 хоккейных команд. Сколько существует способов распределить первое, второе и третье места?
Решение. Первое место займет одна из 8 команд, второе - одна из 7, третье - одна из 6, так как каждая из них не может претендовать одновременно на два призовых места. Поэтому таких способов будет ровно
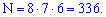
Оба правила обобщаются на случай любого конечного количества действий. В комбинаторике различают три вида различных соединений (комбинаций) элементов фиксированной множества: перестановки, размещения, сочетания. Ниже будут даны их определения с обозначениями, которые наиболее употребительные
Перестановками из  из элементов называются такие их совокупности, отличающихся друг от друга только порядком вхождения элементов. Их обозначают
из элементов называются такие их совокупности, отличающихся друг от друга только порядком вхождения элементов. Их обозначают  и определяют по формуле
и определяют по формуле
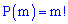
 - факториал числа
- факториал числа  , определяется по правилу
, определяется по правилу 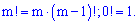
----------------------------
Пример 3. Сколькими способами можно в детсадку поставить группу из 15 детей в ряд?
Решение. На первое место есть возможность поставить одного из 15 детей, на второе одного из 14 и т.д. Общее количество
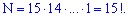
Размещением из 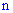 элементов по
элементов по  называются такие совокупности
называются такие совокупности  элементов, отличающихся друг от друга по крайней мере одним элементом или порядком их вхождения (
элементов, отличающихся друг от друга по крайней мере одним элементом или порядком их вхождения (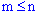 ):
):
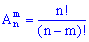
----------------------------
Пример 4. Сколько различных трехзначных чисел можно составить с помощью цифр от 1 до 9 ?
Решение. На первом месте есть возможность поставить одну из 9 цифр, на второе одного из 8 и т.д. Общее количество будет ровно
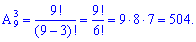
----------------------------
Сочетаниями из 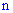 элементов по
элементов по  называются такие комбинации из
называются такие комбинации из  элементов, которые отличаются друг от друга по крайней мере одним элементом (
элементов, которые отличаются друг от друга по крайней мере одним элементом (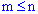 ) :
) :
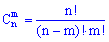
Пример 5. Сколькими способами можно выбрать три цифры из девяти 1, 2, 3, ..., 9?
Решение. Количество всех возможных способов определяем из формулы
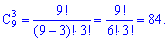
----------------------------
Приклад 6. Из одиннадцати букв азбуки составлено название украинской сказки «Котигорошок». Ребенок, не умеющий читать, рассыпал буквы, а затем собрал в произвольном порядке. Найти вероятность того, что он соберет слово «Котигорошок».
Решение. На здравый смысл получается, что такая вероятность равна нулю, однако это не так. Согласно теории, с одиннадцати букв можно составить различные буквосочетание, отличающиеся между собой только порядком букв, поэтому число всех возможных перестановок равно 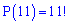
Однако буквы «К» и «О» могут занимать одну из четырех, и одну из двух позиций соответственно, их можно переставлять. Поэтому число благоприятных событий равно
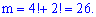
Искомая вероятность примет значение
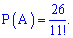
----------------------------
Хорошо разберитесь с приведенными примерами, которые показывают где применять на практике правило сложения, а где умножения; на их основе построен весь следующий материал. Впереди еще много нового следует изучить, здесь только основы теории вероятностей.
]]>
Пусть в условиях эксперимента событие 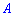 появляется совместно с одним из группы несовместных событий (гипотез)
появляется совместно с одним из группы несовместных событий (гипотез) 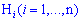 , образующих полную группу
, образующих полную группу 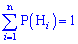 , известны или можно установить априорные вероятности
, известны или можно установить априорные вероятности 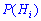 каждой из гипотез и условные вероятности
каждой из гипотез и условные вероятности 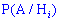 события
события 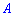 при условии, что осуществилась та или иная гипотеза, тогда вероятность события
при условии, что осуществилась та или иная гипотеза, тогда вероятность события 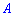 определяется по формуле полной вероятности:
определяется по формуле полной вероятности:

где  – вероятность гипотезы
– вероятность гипотезы 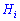 ;
; 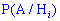 – условная вероятность события
– условная вероятность события 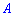 при выполнении гипотезы
при выполнении гипотезы 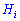 . Приведенная формула называется формулой полной вероятности.
. Приведенная формула называется формулой полной вероятности.
--------------------------------------
Задача 1. В магазине три холодильника в которых заканчивается мороженое. В первом 4 белых и 6 шоколадных, во втором - 2 белых и 8 шоколадных, в третьем - 3 белых и 7 шоколадных. Наугад выбирают холодильник и вынимают из него мороженое. Определить вероятность того, что оно белое.
Решение. Обозначим события следующим образом: 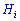 – выбрано
– выбрано 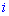 - й холодильник,
- й холодильник, 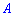 – выбрано белое мороженое
– выбрано белое мороженое
Тогда имеем:
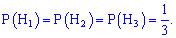
Вероятности, что из каждого холодильника можно извлечь белое мороженое будут равны
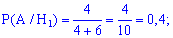
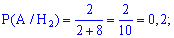
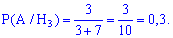
Используя формулу полной вероятности находим:
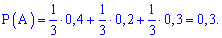
Таким образом вероятность вытащить белое мороженое равна 0,3 или 30%.
--------------------------------------
Задача 2. В офисе есть четыре ноутбука изготовленных компанией 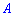 , 6 компанией
, 6 компанией  , 8 компанией
, 8 компанией 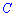 и два, которые производит
и два, которые производит  . Гарантии, что ноутбуки этих компаний будут работать в течение гарантийного срока без ремонта составляют 70%, 80%, 85%, и 55% для каждой из них. Нужно найти вероятность, что выбранный ноутбук будет работать без ремонта в течение гарантийного срока.
. Гарантии, что ноутбуки этих компаний будут работать в течение гарантийного срока без ремонта составляют 70%, 80%, 85%, и 55% для каждой из них. Нужно найти вероятность, что выбранный ноутбук будет работать без ремонта в течение гарантийного срока.
Решение. Обозначим события следующим образом: 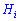 – выбрано ноутбук компании,
– выбрано ноутбук компании, 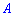 – ноутбук проработает без ремонта.
– ноутбук проработает без ремонта.
Вероятности выбора ноутбука каждой из компаний считаем равносильными их количеству, на основе этого вероятности примут значения:
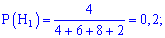
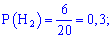
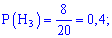
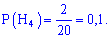
Вероятности, что они будут работать без ремонта равны
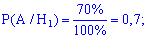
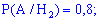
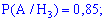
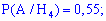
Здесь мы просто переводим проценты в вероятность.
Применяем формулу полной вероятности:
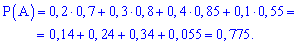
Вероятность безремонтной работы ноутбука равна 0,775.
---------------------------------
ФОРМУЛА БАЙЕСА
Пусть события 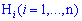 образуют полную группу несовместных событий (
образуют полную группу несовместных событий (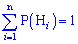 ) и пусть событие
) и пусть событие 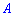 происходит обязательно с одним из них
происходит обязательно с одним из них  . Предположим событие
. Предположим событие 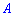 произошло, тогда вероятность того, что оно произошла именно с
произошло, тогда вероятность того, что оно произошла именно с  определяется формулой:
определяется формулой:
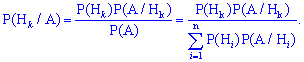
Рассмотрим практическую сторону применения формулы Байеса
-------------------------------
Задача 3. Заданны условия первой задачи. Нужно установить вероятность того, что мороженое извлекли из второго холодильника.
Решение. Выпишем результаты первой задачи, необходимые для вычислений
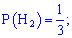
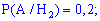
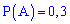
и подставим в формулу Байеса
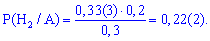
Как можно видеть, вычисления по формуле несложные, главное понять, что и как определяется.
-------------------------------
Задача 4. Для задачи 2 нужно установить вероятность того, что исправный ноутбук принадлежит к компаниям 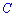 ,
,  .
.
Решение. Выпишем предварительно найдены вероятности
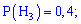
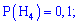
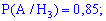
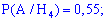
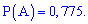
и проведем вычисления по формуле Байеса
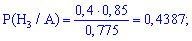
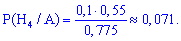
-------------------------------
Задача 5. На склад поступают телефоны трех заводов, причем доля телефонов первого завода составляет 25%, второго - 60%, третьего - 15%. Известно также, что средний процент телефонов без брака для первой фабрики составляет 2%, второй - 4%, третьей - 1%. Найти вероятность того, что:
а) наугад взят телефон окажется с браком;
б) телефон изготовлен на первом заводе, если он бракованный;
в) на каком заводе скорее был изготовлен телефон, если он сделан качественно ?
Решение.
а) Введем для ясности обозначения:
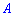 – наугад выбранный телефон оказался бракованным;
– наугад выбранный телефон оказался бракованным;
Предположение: 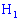 – телефон изготовлен на первой,
– телефон изготовлен на первой,  – второй и
– второй и 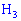 –третий фабрике соответственно. Собития попарно несовместимы и образуют полную группу. Вероятность каждого предположения определяем делением процентной доли продукции ко всей (100%)
–третий фабрике соответственно. Собития попарно несовместимы и образуют полную группу. Вероятность каждого предположения определяем делением процентной доли продукции ко всей (100%)
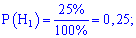
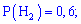
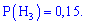
Подобным образом определяем условные вероятности события 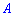
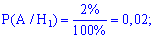
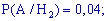
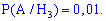
Применим формулу полной вероятности для определения возможности выбора бракованного телефона
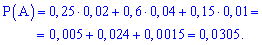
б) для отыскания вероятности применим формулу Байеса
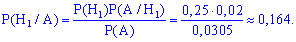
в) чтобы определить, на каком заводе скорее был изготовлен рабочий телефон необходимо сравнить между собой вероятности предположений:
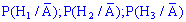
где 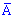 событие (вытащили телефон без брака) противоположна
событие (вытащили телефон без брака) противоположна 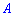 . Для противоположных событий используют формулу
. Для противоположных событий используют формулу
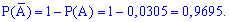
По подобной формуле определяем условные вероятности события 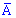 , если только справедливы предположения
, если только справедливы предположения 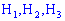



По формуле Байеса находим вероятности
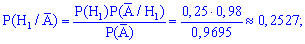
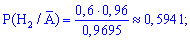
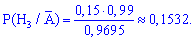
Наибольшую вероятность имеет второе предположение, поэтому телефон скорее всего был изготовлен на втором заводе.
-------------------------------
Задач на нахождение полной вероятности и применения формулы Байеса в литературе и интернете множество. Стоит ввести в гугле нужный запрос и вам тут же будет предложено множество материалов к выбору. Поэтому освоить данный материал не трудно, стоит лишь внимательно (без паники) разобраться с приведенными примерами и подобными. Все остальные решаются по аналогичной схеме.
]]>
 во всех испытаниях одна и та же, во втором случае она меняется от опыта к опыту.
во всех испытаниях одна и та же, во втором случае она меняется от опыта к опыту.
Пусть для каждого опыта вероятность появления события  равна
равна 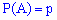 , вероятность противоположного события определяется зависимостью
, вероятность противоположного события определяется зависимостью
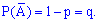
Нужно найти вероятность появления события  ровно
ровно  раз в серии из
раз в серии из 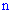 испытаний. При этом следует отметить, что событие
испытаний. При этом следует отметить, что событие  в серии опытов может чередоваться любым способом, главное чтобы исполнилась ровно
в серии опытов может чередоваться любым способом, главное чтобы исполнилась ровно  раз.
раз.
Результаты испытаний для удобства обозначаем буквой  в случае появления события и
в случае появления события и 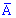 для противоположного.
для противоположного.
Испытания в которых  происходит
происходит  раз и не происходит (
раз и не происходит (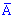 )
) 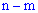 раз по определению будут благоприятными. Их количество
раз по определению будут благоприятными. Их количество 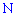 равно количеству способов выбора
равно количеству способов выбора  элементов с
элементов с 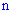 и определяется по формуле сочетания
и определяется по формуле сочетания
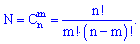
Определим вероятность благоприятной комбинации (в серии из 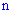 испытаний появления события
испытаний появления события  ровно
ровно  раз). Для простоты записи, рассмотрим случай, когда событие
раз). Для простоты записи, рассмотрим случай, когда событие  произошло в первых опытах и не состоялось в остальных
произошло в первых опытах и не состоялось в остальных 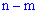 . Схематично его можно обозначить следующим образом, а вероятность найти по теореме умножения вероятностей
. Схематично его можно обозначить следующим образом, а вероятность найти по теореме умножения вероятностей

для других благоприятных испытаний 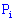 и вероятности будут такие же, только порядок их в серии из экспериментов будет постоянно меняться
и вероятности будут такие же, только порядок их в серии из экспериментов будет постоянно меняться
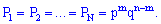
Все благоприятные испытания являются попарно несовместимы, поэтому для нахождения общей вероятности их нужно просуммировать

или
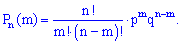
Вывел ее впервые швейцарский математик Якоб Бернулли (1654 г.-1705 г.).
Если просуммировать вероятности всех испытаний в которых событие  может произойти от нуля до
может произойти от нуля до 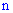 раз в серии
раз в серии 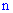 испытаний, то получим полную вероятность
испытаний, то получим полную вероятность
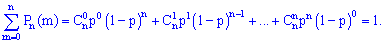
Слагаемые этой суммы совпадают по виду с расписанием бинома Ньютона
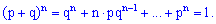
Легко убедится, что
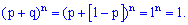
В литературе можно встретить термин "биномиальное распределение вероятностей", это как раз множество всех вероятностей, которые просуммированы выше.
Как последствия, из формулы Бернулли выводятся следующие формулы для популярных для практики задач:
1) вероятность появления события  "хотя бы один раз" в серии из
"хотя бы один раз" в серии из 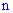 испытаний
испытаний
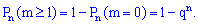
2) вероятность появления события  "хотя бы определенное количество
"хотя бы определенное количество 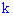 раз" в серии из
раз" в серии из 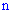 испытаний вычисляют по формуле
испытаний вычисляют по формуле
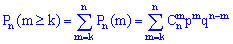
или согласно свойству биномиального разложения вероятностей
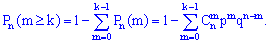
На основе данной зависимости вводят в рассмотрение сквозную функцию, которая дает возможность определить возможное количество появления события  в серии из
в серии из 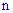 испытаний
испытаний
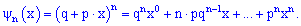
По свойству сквозной функции множители при  степени переменной (
степени переменной (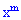 ) равны вероятности появления события
) равны вероятности появления события  в серии из
в серии из 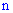 опытов ровно
опытов ровно  раз. Это легко проследить по формуле суммирования вероятностей всех возможных испытаний по схеме Бернулли.
раз. Это легко проследить по формуле суммирования вероятностей всех возможных испытаний по схеме Бернулли.
Если вероятности появления события в каждом опыте разные 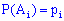 , а противоположного равны
, а противоположного равны 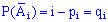 то по свойствам сквозной функции вероятность события
то по свойствам сквозной функции вероятность события  произойти
произойти  раз в серии из
раз в серии из 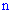 опытов равна множителю при
опытов равна множителю при 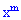 в расписании функции по степеням
в расписании функции по степеням
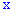
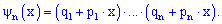
Она достаточно часто встречается при решении задач, в которых вероятности появления события  в каждом последующем опыте меняются и позволяет при небольшом количестве
в каждом последующем опыте меняются и позволяет при небольшом количестве  появления события
появления события  быстро найти вероятность (решение задачи).
быстро найти вероятность (решение задачи).
Вероятное количество 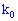 появлений события
появлений события  в схеме Бернулли лежит в интервале
в схеме Бернулли лежит в интервале
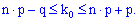
Для применения схемы Бернулли нужно, чтобы выполнялись три условия:
1) опыты должны быть независимы между собой;
2) каждый опыт должен иметь два результата  ,
, 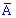 и никаких других вариантов;
и никаких других вариантов;
3) вероятность появления события  должна быть одинаковой для каждого следующего опыта.
должна быть одинаковой для каждого следующего опыта.
Рассмотрим решения типичных для данной схемы задач.
-----------------------------
Пример 1. В тире стрелок проводит 7 выстрелов по мишени с вероятностью попадания каждого 0,8. Какова вероятность того, что будет: а) ровно 4 попадания б) не менее 5 попаданий в) не более двух попаданий.
Решение. а) проводится 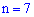 независимых друг от друга испытаний с вероятностью попадания в мишень в каждом из них
независимых друг от друга испытаний с вероятностью попадания в мишень в каждом из них 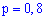 . Вероятность того, что будет точно
. Вероятность того, что будет точно 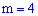 попаданий вычисляем по формуле Бернулли:
попаданий вычисляем по формуле Бернулли:
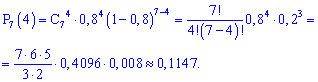
б) событие 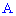 , которое заключается в том, что при
, которое заключается в том, что при 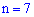 выстрелах будет не менее 5 попаданий, можно рассматривать как сумму трех несовместных событий:
выстрелах будет не менее 5 попаданий, можно рассматривать как сумму трех несовместных событий:  – 5 попаданий из 7, событие
– 5 попаданий из 7, событие  – 6 попаданий с 7 и
– 6 попаданий с 7 и  – все 7 выстрелов метки.
– все 7 выстрелов метки.
По формуле Бернулли находим вероятности событий
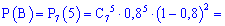
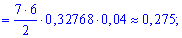
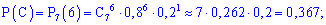
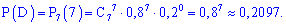
Тогда вероятность события 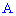 равна сумме найденных вероятностей
равна сумме найденных вероятностей
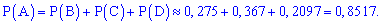
в) Подобным образом, вероятность события  – не более двух попаданий при семи выстрелах можно вычислить, как сумму вероятностей трех событий:
– не более двух попаданий при семи выстрелах можно вычислить, как сумму вероятностей трех событий:
 – 2 попадания из 7,
– 2 попадания из 7,
 – 1 из 7 ,
– 1 из 7 ,
 – ни одного попадания из 7 выстрелов (7 промахов).
– ни одного попадания из 7 выстрелов (7 промахов).
На практике студенты часто забывают рассматривать событие - подобное отсутствию попадений  , поэтому не делайте подобных ошибок и хорошо запомните возможность возникновения такого варианта. Вероятности находим по знакомой уже формуле
, поэтому не делайте подобных ошибок и хорошо запомните возможность возникновения такого варианта. Вероятности находим по знакомой уже формуле
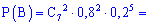
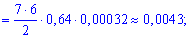
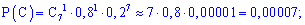
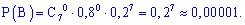
Суммируя вероятности получим

Однако, события 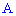 (не более двух попаданий при семи выстрелах) и (не менее 5 попаданий при семи выстрелах) противоположны друг другу, поэтому
(не более двух попаданий при семи выстрелах) и (не менее 5 попаданий при семи выстрелах) противоположны друг другу, поэтому
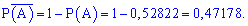
-----------------------------
Пример 2. Монета подбрасывают пять раз. Найти вероятность того, что герб выпадет не более трех раз.
Решение. Вероятность выпадения герба или решки считаем независимым событием с вероятностью 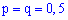 . По аналогии с предыдущей задачей, искомая вероятность равна сумме трех следующих
. По аналогии с предыдущей задачей, искомая вероятность равна сумме трех следующих
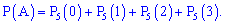
Чтобы не искать столько слагаемых, из приведенных выше формул получим простую
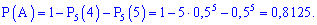
-----------------------------
Пример 3. Вероятность появления события в одном опыте равна 0,4. Сколько нужно провести опытов, чтобы вероятное количество появления события была равна 20.
Решение. Согласно условия выписываем данные
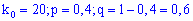
и проводим расчеты согласно неравенству
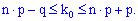
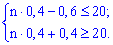
С него получим
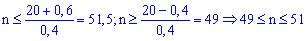
три числа 49,50,51.
-----------------------------
Пример 4. Три биатлониста независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого равна 0,9, для второго - 0,85, для третьего - 0,8. Найти вероятность того, что будут закрыты две мишени из трех.
Решение. Вероятности попадания для стрелков разные, поэтому применяем образующую функцию. Для нее входные данные примут значения
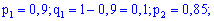
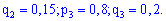
После подстановки и разложения в ряд получим
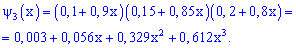
Искомая вероятность входит в расписание множителем при 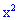
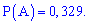
Из этого примера также легко убедиться, что сумма всех множителей при степенях 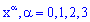 равна полной вероятности (единицы).
равна полной вероятности (единицы).
-----------------------------
Схема Бернулли на практике не сложная, важно уловить как в вычислениях реализовать задачи вида "не более  раз", "не менее
раз", "не менее  раз", "ровно
раз", "ровно  раз" с
раз" с 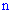 . Как только Вы это поймете, все остальное сведется к суммирования, умножению и возведения в степень.
. Как только Вы это поймете, все остальное сведется к суммирования, умножению и возведения в степень.
]]>
ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА
Вероятность того, что в 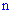 независимых испытаниях с вероятностью появления события
независимых испытаниях с вероятностью появления события 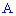 равной
равной 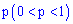 событие
событие 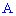 наступит ровно
наступит ровно 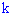 раз (безразлично в какой последовательности) определяется по приближенной формуле
раз (безразлично в какой последовательности) определяется по приближенной формуле
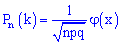
где
 – Функция Гаусса,
– Функция Гаусса,
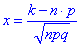 – аргумент функции Гаусса;
– аргумент функции Гаусса;
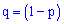 – вероятность противоположного события
– вероятность противоположного события 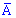 .
.
Формулу 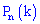 называют локальной формулой Лапласа.
называют локальной формулой Лапласа.
Функция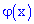 обладает следующими свойствами:
обладает следующими свойствами:
1) она является четной функцией 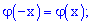 ;
;
2) для значений аргумента больше четырех она сколь угодно мала 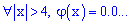
Теорему Лапласа рекомендуется применять при значениях произведения больше девяти
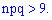
ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА
Вероятность, что в 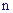 независимых испытаниях событие
независимых испытаниях событие 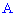 с вероятностью появления
с вероятностью появления 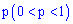 наступит не менее
наступит не менее 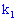 раз и не более
раз и не более 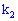 (независимо от последовательности появления) приближенно определяется зависимостью
(независимо от последовательности появления) приближенно определяется зависимостью
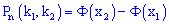
где 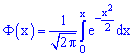 – интегральная функция Лапласа;
– интегральная функция Лапласа;
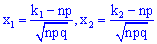 – аргументы интегральной функции распределения;
– аргументы интегральной функции распределения;
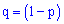 – вероятность невыполнения события
– вероятность невыполнения события 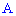 .
.
Функция 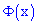 обладает следующими свойствами:
обладает следующими свойствами:
1) она является нечетной функцией
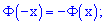
2) для аргументов больше пяти она равна 0,5
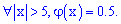
Значение обеих функций 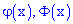 находят из таблиц в которых функции с достаточной точностью протабульовани.
находят из таблиц в которых функции с достаточной точностью протабульовани.
--------------------------------
Рассмотрим задачи на применение каждой из теорем.
Пример 1. Есть 100 лунок по которым случайным образом разбрасывают 30 шариков. Каждый шарик с равной вероятностью может попасть в любую лунку (в одну лунку попадает не более одного шарика). Найти вероятность того, что в выбранную лунку попадет ровно один шарик.
Решение. Проводится 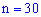 независимых бросков шариков с одинаковой вероятностью попадания при каждом броске
независимых бросков шариков с одинаковой вероятностью попадания при каждом броске
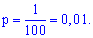
Вероятность попадания в лунку ровно одного шарика определим по локальной формулой Лапласа:
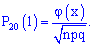
Для этого определяем составляющие
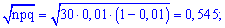
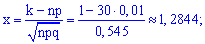
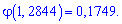
и подставим в зависимость
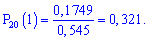
--------------------------------
Пример 2. Проводится 200 независимых опытов с вероятностью успеха в каждом 24%. Какова вероятность успешного проведения 50 опытов?
Решение. По условию 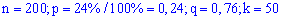
находим составляющие формулы Лапласа
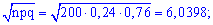
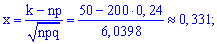
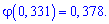
Подставляя в формулу, находим
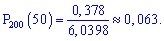
--------------------------------
Пример 3. Вероятность выхода из строя за смену одного станка равна 0,1. Определить вероятность выхода из строя от 2 до 13 станков при наличии 100 станков.
Решение. Записываем входные данные
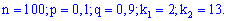
Для подобных примеров применяем интегральную формулу Муавра-Лапласа и находим вероятность
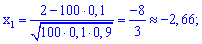

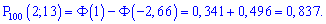
--------------------------------
Решение задач по приведенным теоремам позволяет при большом количестве испытаний находить приближенное значение вероятности. Локальная теорема необходима при определении конкретного количества появления событий, интегральная теорема Муавра-Лапласа - в случаях, когда задан диапазон возможного количества появлений события. Таблицы табулирования функций, применяемых в формулах можно найти в сборниках по теории вероятностей и интернете.
]]>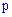 появления события
появления события 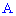 в отдельном испытании достаточно близка к нулю
в отдельном испытании достаточно близка к нулю 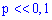 , то даже при больших
, то даже при больших 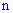 значениях количества испытаний вероятность, вычисляемая по локальной теореме Лапласа, оказывается недостаточно точной. В таких случаях используют формулу, выведенную Пуассоном.
значениях количества испытаний вероятность, вычисляемая по локальной теореме Лапласа, оказывается недостаточно точной. В таких случаях используют формулу, выведенную Пуассоном.
ТЕОРЕМА ПУАССОНА
Если вероятность 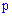 наступления события
наступления события 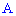 в каждом испытании постоянна, но достаточно мала, число независимых испытаний
в каждом испытании постоянна, но достаточно мала, число независимых испытаний 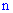 достаточно велико, при этом сочетания
достаточно велико, при этом сочетания  меньше десяти то вероятность того, что в количестве
меньше десяти то вероятность того, что в количестве 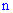 испытаниях событие
испытаниях событие 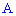 наступит ровно
наступит ровно 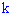 раз примерно равна
раз примерно равна
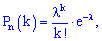
где 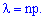
Для формулы Пуассона используют таблицы табулирования функции 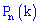 .
.
-------------------------------
Рассмотрим примеры типичных для студентов задач.
Пример 1. Автобиография писателя издается тиражом в 1000 экземпляров. Для каждой книги вероятность быть неправильно сброшюрованной равна 0,002. Найти вероятность того, что тираж содержать ровно 7 бракованных книг.
Решение. Проверим выполнение условия теоремы Пуассона. Для входных значений
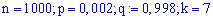
получим
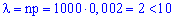
что условия выполняются.
По табличным значениям функции Пуассона находим вероятность
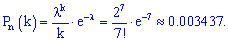
Применения к этому событию локальную теорему Лапласа получим
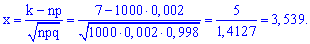
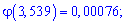
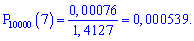
Точное значение вероятности определяем по формуле Бернулли
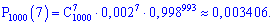
Из анализа трех методов следует, что формула Пуассона дает более точнее приближения, чем формула Лапласа. Именно поэтому ее рекомендуют применять для отыскания вероятности в такого сорта задачах.
-------------------------------
Пример 2. Вероятность изготовления нестандартной детали равна 0,004. Найти вероятность того, что среди 1000 деталей окажется 5 нестандартных.
Решение. Имеем даные 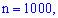
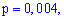 , которые удовлетворяют требования теоремы Пуассона
, которые удовлетворяют требования теоремы Пуассона 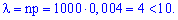 По таблице функции Пуассона при
По таблице функции Пуассона при 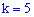 получим:
получим:
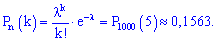
Найдем вероятность того же события по локальной теореме Лапласа.
Для 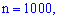
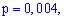
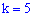 ,
,
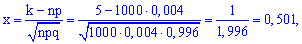
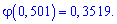
искомая вероятность: 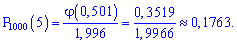
Точное значение вычисляем согласно формулы Бернулли:
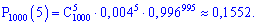
Таким образом, формула Пуассона дает гораздо более точное приближение, чем формула Лапласа.
-------------------------------
Пример 3. Станок штампует детали. Вероятность того, что изготовленная деталь бракованная, равна 0,02. Какова вероятность того, что среди 200 деталей окажется 5 бракованных?
Решение. Есть 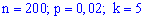 , есть удовлетворяются требования теоремы
, есть удовлетворяются требования теоремы
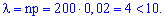
По таблице функции Пуассона при 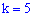 получим:
получим:
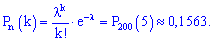
----------------------------------------------
Используйте формулу Пуассона в тех задачах, где она более уместна. Всегда проверяйте выполнения условия теоремы Пуассона, при значениях которые не удовлетворяют условие  формула дает большую погрешность при вычислении вероятности. Для проверки результата применяйте формулу Бернулли, она более точна и с ее результатом найденную вероятность по формуле Пуассона лучше всего сравнивать. Если погрешность невелика, тогда Вы все сделали правильно, в противном случае придется вычислять снова или найти слабое место и исправить ошибки.
формула дает большую погрешность при вычислении вероятности. Для проверки результата применяйте формулу Бернулли, она более точна и с ее результатом найденную вероятность по формуле Пуассона лучше всего сравнивать. Если погрешность невелика, тогда Вы все сделали правильно, в противном случае придется вычислять снова или найти слабое место и исправить ошибки.