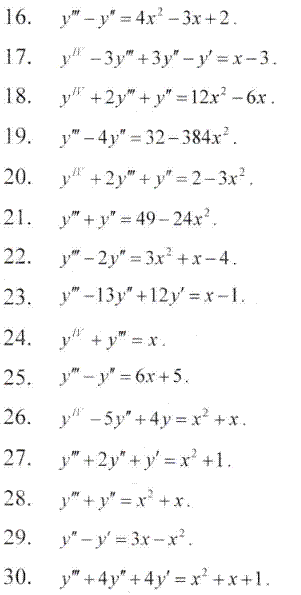Если независимая переменная одна, то уравнение называется обыкновенным; если независимых переменных две или более, то уравнение называется дифференциальным уравнением в частных производных. С целью получить високовалифицированих специалистов во всех ВУЗах где изучают точные дисциплины обязательно курс дифференциальных уравнений. Для одних студентов теория дается тяжело, практика еще с горем пополам, для других тяжелая и теория, и практика. Если анализировать дифференциальные уравнения с практической стороны, то для их вычислений Вам нужно только хорошо уметь интегрировать и брать производные. Все остальные преобразования сводятся к нескольким схемам которые можно понять и изучить. Ниже изучем основные определения и метод решения простых ДР.
Теория дифференциальных уравнений
Определение: Обычным дифференциальным уравнением называют уравнение, которое в себе связывает независимую переменную х, функцию у(х) , ее производные у'(х), уn(х) и имеет общий вид F(x,y(x),y' (x), …, yn(x))=0
Дифференциальным уравнением (ДР) называется или обычное дифференциальное уравнение, или дифференциальное уравнение в частных производных. Порядок дифференциального уравнения определяется порядком старшей производной (n), которая входит в данное дифференциальное уравнение.
Общим решением дифференциального уравнения называется функция, которая содержит столько постоянных, каков порядок дифференциального уравнения, и подстановка которой в данное дифференциальное уравнение превращает его в тождество, то есть имеет вид y=f(x, C1, C2, …, Cn).
Общее решение, которое не разрешено относительно у(х) и имеет вид F(x,y,C1,C2, …, Cn)=0 называется общим интегралом дифференциального уравнения.
Решение найденное из общего при фиксированных значениях постоянных C1,C2, …, Cn называется частным решением дифференциального уравнения.
Одновременное задания дифференциального уравнения и соответствующего количества начальных условий называется задачей Коши.
F(x,y,C1,C2, …, Cn)=0
y(x0)=y0;
….
yn(x0)=yn(0)
Обыкновенным дифференциальным уравнением первого порядка называется уравнение вида
F(x, y, y')=0. (1)
Интегралом уравнения (1) называется cоотношение вида Ф (x,y)=0, если каждая неявно заданная им непрерывно-дифференциированая функция является решением уравнения (1).
Уравнение которое имеет вид (1) и не может быть сведено к простому виду называется уравнением, неразрешимим относительно производной. Если его можно записать в виде
y' = f(x,y), то оно называется решенным уравнением относительно производной.
Задача Коши для уравнения первого порядка содержит только одну начальную условие и имеет вид:
F(x,y,y')=0
y(x0)=y0.
Уравнения вида
M(x,y)dx+N(x,y)dx=0 (2)
где переменные x i y является "симметричными": можно предполагать, что x - независимая, а y - зависимая переменная, или наоборот, y - независимая, а x - зависимая переменная, называется уравнением в симметричной форме.
Геометрический смысл дифференциального уравнения первого порядка
y'=f(x,y) (3)
заключается в следующем.
Данное уравнение устанавливает связь (зависимость) между координатами точки (x;y) и угловым коэффициентом y' касательной к интегральной кривой, проходящей через эту точку. Таким образом, уравнение y'= f(x,y) представляет собой совокупность направлений (поле направлений) на декартовой плоскости Oxy.
Кривая построенная на точках в которых направление поля одинаково называется изоклиной. Изоклины можно использовать для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить производную равную постоянной y'=С
f(x, y)=С - уравнение изоклины..
Интегральной линией уравнения (3) называется график решения этого уравнения.
Обычные дифференциальные уравнения, решения которых можно задать аналитически y=g(x), называются интегрируемыми уравнениями.
Уравнения вида
M0(x)dx+N0(y)dy=0 (3)
называются уравнениями с раздельными сменными.
Из них и начнем знакомство с дифференциальными уравнениями. Процесс нахождения решений ДР называют интегрированием дифференциального уравнения.
Уравнения с разделенными переменными
Пример 1. Найти решение уравнения y'=x .
Выполнить проверку решения.
Решение: Запишем уравнение в дифференциалах
dy/dx=x или dy=x*dx.
Найдем интеграл правой и левой части уравнения
int(dy)=int(x*dx);
y=x2/2+C.
Это и есть интеграл ДР.
Проверим его правильность, вычислим производную функции
y'=1/2*2x+0=x.
Как можно убедиться получили исходное ДР, следовательно вычисления верны.
Мы только что нашли решение дифференциального уравнения первого порядка. Это именно проще уравнения, которое можно себе представить.
Пример 2. Найти общий интеграл дифференциального уравнения
(x+1)y'=y+3
Решение: Запишем исходное уравнение в дифференциалах
(x+1)dy=(y+3)dx.
Полученное уравнение сводим к ДР с разделенными переменными
![]()
Все что осталось это взять интеграл от обеих частей
![]()
По табличными формулами находим
ln|y+3|=ln|x+1|+C.
Если экспонировать обе части, то получим
y+3=e ln|x+1|+C или y=e ln|x+1|+C-3.
Такая запись является правильной, но не является компактной.
На практике применяют другой прием, при вычислении интеграла постоянную вносят под логарифм
ln|y+3|=ln|x+1|+ln(C).
По свойствам логарифма это позволяет свернуть два последних слагаемых
ln|y+3|=ln(С|x+1|).
Теперь при экспонировании решение дифференциального уравнения станет компактное и легко читаемое
y= С|x+1|+3
Запомните это правило, на практике оно применяется как эталон вычислений.
Пример 3. Решить дифференциальное уравнение
y'=-y*sin(x).
Решение:Запишем уравнение в дифференциалах
dy/dx= y*sin(x)
или после перегруппировки множителей в виде уравнения с разделенными переменными
dy/ y=-sin(x)dx.
Осталось проинтегрировать уравнение
int(1/y,y)=-int(sin(x), x);
ln|y|=cos(x)-ln(C).
Константу удобно внести под логарифм, да еще и с отрицательным значением, чтобы перенеся в левую часть получить
ln|С*y|=cos(x).
Экспонируем обе части зависимости
С*y=exp(cos(x)).
Это и есть общий интеграл дифференциального уравнения. Его можно оставить как есть, а можно постоянную перенести в правую сторону
![]()
Вычисления не сложные, интегралы тоже в большинстве случаев можно найти по табличным формулам интегрирования.
Пример 4. Решить задачу Коши
y'=y+x, y(1)=e3-2.
Решение:Здесь уже предварительные преобразования не пройдут. Однако уравнение линейное и довольно простое. В таких случаях нужно ввести новую переменную
z=y+x.
Помня, что y=y(x) найдем производную от z.
z'= y'+1,
откуда выражаем старую производную
y'= z'-1.
Подставим это все в исходное уравнение
z'-1=z или z'=z+1.
Распишем дифференциальное уравнения через дифференциалы
dz=(z+1)dx.
Отделяем переменные в уравнении
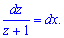
Осталось вычислить простые интегралы, которые под силу каждому
![]()
Экспонируем зависимость, чтобы избавиться от логарифма при функции
z+1=ex+Сабо z=ex+1-1
Не забываем вернуться к выполненной замене
z=x+y= ex+С-1,
отсюда выписываем общее решение дифференциального уравнения
y= ex+С-x-1.
Найти решение задачи Коши в ДР в данном случае не сложно. Выписываем условие Коши
y(1)=e3-2
и подставляем в только что найденное решение
e1+С-1-1= e3-2.
Отсюда получим условие для вычисления постоянной
1+С=3; С=3-1=2.
Теперь можем записать решение задачи Коши (частичный решение ДР)
y= ex+2-x-1.
Если Вы хорошо умеете интегрировать, с производной у Вас дела тоже на высоте, тогда тема дифференциальных уравнений для Вас не будет препятствием в образовании.
В дальнейшем обучении Вам необходимо изучить несколько важных схем, чтобы научиться различать уравнения и знать, какая замена или методика работает в каждом случае.
После этого Вас ждут однородные и неоднородные ДР, дифференциальные уравнения первого и высших порядков. Чтобы не нагружать Вас теорией в следующих уроках мы будем приводить только тип уравнений и краткую схему их вычислений. Всю теорию Вы можете почитать из методических рекомендаций для изучения курса "Дифференциальные уравнения" (2014) авторы Бокало Николай Михайлович, Доманская Елена Викторовна, Чмырь Оксана Юрьевна. Можете использовать другие источники, содержащие понятны Вам объяснения теории дифференциальных уравнений. Готовые примеры для диф. уравнений взяты из программы для математиков ЛНУ им. И. Франка.
Мы знаем, как решить дифференциальные уравнения и постараемся в легкий способ привить эти знания Вам.
Сферы применения дифференциальных уравнений были в общем очерчены на предыдущем уроке. Здесь речь пойдет об одном из самых простых (в плане вычислений) типов ДУ первого порядка среди всех возможных уравнений что Вас ждут. Начнем с базовых понятий теории которые Вы должны знать и мы будем использовать в терминологии. Для одних это не нужно, потому что они ищут готовые ответы по дифференциальным уравнениям и думают, что таким образом решат все проблемы. Но это ошибка, потому что не знание элементарных понятий по теории ДУ сравнимо с тем, что Вы пытаетесь говорить, предварительно не изучив звуки и алфавит.
Дифференциальное уравнение первого порядка, которое можно записать формулой
N(х)dx+М(у)dy=0 (1)
называют уравнением с разделенными переменными.
Их не трудно обнаружить среди других уравнений, основной признак - множители при dx и dy являются функциями (константами), которые зависят только от х при множителе dx и у при dy.
Чтобы найти общее решение (общий интеграл) уравнения с разделенными переменными необходимо проинтегрировать уравнение (1)
Int(N(x), x) + Int(M(y),y) = С,
Для понимания дифференциальное уравнение (1) можно принимать, как условие равенства нулю полного дифференциала некоторой функции двух переменных U(x,y)
Отсюда следует что функция U(x,y)=С=const равна постоянной.
Дифференциальное уравнение вида
f1(x)*g1(y)dx+f2(x)*g2(y)dy=0 (2)
называют дифференциальным уравнением с разделяющимися переменными в симметричной форме.
В уравнении (2) коэффициенты при дифференциалах dx и dy является произведениями двух функций: одна зависит только от x, а вторая - от y. В области, где g1(y), f2(x) принимают отличные от нуля значения в уравнение с разделяющимися переменными (2) сводится к уравнению с разделенными переменными
Звучит как игра слов: разделенными, разделяющимися, однако между ними как видите есть маленькая разница, и теперь Вы ее знаете.
Рассмотрим типичные для практики задания на диф. уравнения первого порядка, которые в достаточно простой способ можно свести к уравнениям с разделенными переменными.
Пример 1 Решить дифференциальное уравнение
![]() Решение:Имеем дифференциальное уравнение первого порядка, по теории его можно назвать уравнением с разделяющимися переменными или уравнением в дифференциалах. Для его упрощения сгруппируем слагаемые, содержащие dx, dy по разные стороны знака равенства
Решение:Имеем дифференциальное уравнение первого порядка, по теории его можно назвать уравнением с разделяющимися переменными или уравнением в дифференциалах. Для его упрощения сгруппируем слагаемые, содержащие dx, dy по разные стороны знака равенства
![]()
Далее выделим общие множители для каждой суммы и перепишем уравнение в дифференциалах в форме
![]()
После этого все, что содержит y переносим к dy, то же самое проделываем с множителями которые содержат переменную x.
В результате придем к дифференциальному уравнению с разделенными переменными
![]()
Теперь посмотрите почему данное уравнение называется уравнением с разделенными переменными? - Возле dx имеем функцию зависимую только от "икс", у dy - только от y.
Проинтегрируем дифференциальное уравнение
![]()
Выносим множители, чтобы при переменной в знаменателе стояли единицы. Также, чтобы в числителе получить дифференциалы знаменателя умножаем обе части на 2
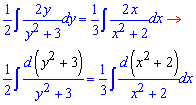
Это позволяет упростить вычисления интеграла ДУ (после интегрирования получить логарифмы)
![]()
Константу рекомендуем внести в логарифм, для этого записывайте всегда ее в виде C1=ln(C)
![]()
Чтобы раскрыть логарифмическое уравнение экспонируем (находим экспоненту) правую и левую сторону зависимости
![]() (3)
(3)
Также выделяем значение функции
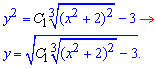
Конечная запись имеет двойной корень и является общим решением уравнения с разделяющимися переменными. Это не совсем хороший тон подавать ответ, лучше решение оставить в виде формулы (3), только тройку перенести в правую сторону.
Пример 2 Найти общий интеграл дифференциального уравнения
![]() Решение:Имеем уравнение в дифференциалах первого порядка. Разделим в уравнении переменные, содержащиеся при dx, dy и перенесем их по разные стороны знака равенства
Решение:Имеем уравнение в дифференциалах первого порядка. Разделим в уравнении переменные, содержащиеся при dx, dy и перенесем их по разные стороны знака равенства
![]()
С первых скобок выносим общий для двух слагаемых множитель y за скобки
![]()
Далее разделим множители так, чтобы при dy получить функцию только от y, а при dx - функцию аргумента x. В результате получим дифференциальное уравнение с разделенными переменными
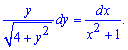
После интегрирования

получим корневую зависимость для y и арктангенс в результате вычисления интеграла по аргументу (правая сторона).
![]()
Общий интеграл можем оставить в такой форме или перенести артангенс в левую часть зависимости.
Так же можем записать решение дифференциального уравнения в виде зависимости y(x) (явном виде). Для этого возведем обе части к квадрату
![]()
и перенеся сталую в правую сторону, вычислим корень квадратный
![]()
Это и есть искомое решение дифференциального уравнения.
Пример 3 Решить дифференциальное уравнение
![]() Решение:Данное ДУ первого порядка необходимо свести под правило решения уравнений с разделенными переменными. Для этого второе слагаемое, что со знаком минус, переносим в правую сторону от знака равенства
Решение:Данное ДУ первого порядка необходимо свести под правило решения уравнений с разделенными переменными. Для этого второе слагаемое, что со знаком минус, переносим в правую сторону от знака равенства
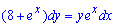
и разделяем переменные
![]()
Проинтегрируем левую и правую сторону зависимости
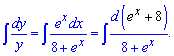
В результате придем к логарифмическому уравнению вида
![]()
И снова обращаем Ваше внимание на то что в таком виде как правило не записывают.
Целесообразно, для компактности конечного решения, постоянную вносить под логарифм, то есть в форме
![]()
Взяв экспоненту от правой и левой части формулы придем к конечному виду решения дифференциального уравнения
![]()
Как Вы могли убедиться примеры достаточно просты, методика вычислений ДУ з разделенными переменными легкая для изучения.
Пример 4 Решить дифференциальное уравнение![]() Решение: Одно из слагаемых (не содержит производной) переносим за знак равенства
Решение: Одно из слагаемых (не содержит производной) переносим за знак равенства
![]()
и записываем уравнение в дифференциалах..
![]()
Следующим шагом сводим зависимость к дифференциальному уравнению с разделенными переменными.
Для заданного уравнения всего лишь перекрестным делением записываем корни в знаменатели
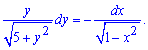
В таком виде можем интегрировать уравнения
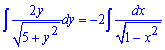
Левая сторона содержит функцию которая при иртегрировании даст корневую зависимость, для правой стороны по формулам получим арксинус.
![]()
Выполняем манипуляции с корнем, чтобы получить зависимость вида y=y(x)
![]()
Решение дифференциального уравнения будет иметь вид
![]()
На этом вводный урок закончен и основные выводы Вы должны сделать самостоятельно.
Для закрепления темы рекомендуем самостоятельно решить несколько из следующих примеров.
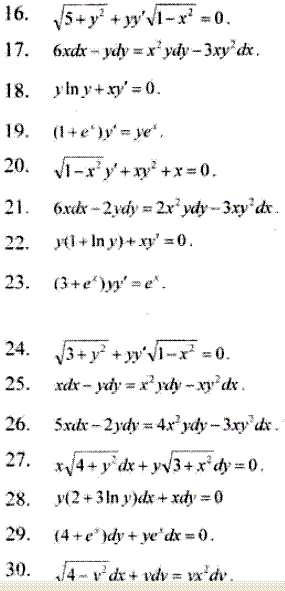 Хотите верьте, а хотите - нет, но это самый простой тип дифференциальных уравнений, с которым Вам придетсяиметь дело на контрольной, экзаменах, практических занятиях, модулях. Это можно сказать важнейшая часть, поскольку сложные дифференциальные уравнения придется упрощать и сводить к уравнениям с разделенными переменными.
Хотите верьте, а хотите - нет, но это самый простой тип дифференциальных уравнений, с которым Вам придетсяиметь дело на контрольной, экзаменах, практических занятиях, модулях. Это можно сказать важнейшая часть, поскольку сложные дифференциальные уравнения придется упрощать и сводить к уравнениям с разделенными переменными.
Схему вычислений должны заучить и знать на зубок - это один из основных методов решения сложных примеров на диф. уравнения.
Уравнения вида P(x,y)dx+Q(x,y)dy=0, где функции P(x,y) і Q(x,y) являются однородными функциями одного порядка называют однородным дифференциальным уравнением (ОДР).
Схема решения однородного дифференциального уравнения
1. Сначала нужно применить подстановку y=z*x, где z=z(x) – новая неизвестная функция (таким образом исходное уравнение сводится к дифференциальному уравнению с разделяющимися переменными.
2. Производная произведения равна y'=(z*x)'=z'*x+z*x'=z'*x+z или в дифференциалах dy=d(zx)=z*dx+x*dz.
3. Далее подставляем новую функцию у и ее производную y' (или dy) в ДУ с разделяющимися переменными относительно x та z.
4. Решив дифференциальное уравнение с разделяющимися переменными, сделаем обратную замену y=z*x, поэтому z= y/х, и получим общее решение (общий интеграл) дифференциального уравнения.
5. Если задано начальное условие y(x0)=y0, то находим частное решение задачи Коши. В теории все звучит легко, однако на практике не у всех так весело получается решать дифференциальные уравнения. Поэтому для углубления знаний рассмотрим распространенные примеры. На легких задачах нет особо Вас научить, поэтому сразу перейдем к более сложным.
Вычисления однородных дифференциальных уравнений первого порядка
Пример 1. Решить дифференциальное уравнение
![]()
Решение: Делим правую сторону уравнения на переменную, которая стоит множителем возле производной. В результате придем к однородного дифференциального уравнения 0 порядка
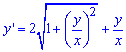
И здесь многим пожалуй стало интересно, как определить порядок функции однородного уравнения?
Вопрос достаточно уместен, а ответ на него следующий:
в правую сторону подставляем вместо функции и аргумента значение t*x, t*y. При упрощении получают параметр "t" в определенном степени k, его и называют порядком уравнения. В нашем случае "t" сократится, что равносильно 0-м степени или нулевом порядке однородного уравнения.
Далее в правой стороне можем перейти к новой переменной y=zx; z=y/x .
При этом не забываем выразить производную "y" через производную новой переменной. По правилу части находим
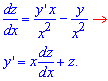
Уравнения в дифференциалах примет вид
![]()
Совместные слагаемые в правой и левой части сокращаем и переходим к дифференциальному уравнению с разделенными переменными.
![]()
Проинтегрируем обе части ДУ
![]()
Для удобства дальнейших преобразований постоянную сразу вносим под логарифм
![]()
По свойствам логарифмов полученное логарифмическое уравнение эквивалентно следующему
![]()
Эта запись еще не решение (ответ), необходимо вернуться к выполненной замене переменных
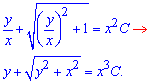
Таким образом находят общее решение дифференциальных уравнений. Если Вы внимательно читали предыдущие уроки, то мы говорили, что схему вычисления уравнений с разделенными переменными Вы должны уметь применять свободно и такого рода уравнения придется вычислять для более сложных типов ДУ.
Пример 2. Найти интеграл дифференциального уравнения
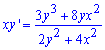
Решение:Схема вычислений однородных и сводных к ним ДУ Вам тепер знакома. Переносим переменную в правую сторону уравнения, а также в числителе и знаменателе выносим x2, как общий множитель
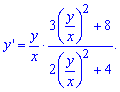
Таким образом получим однородное ДУ нулевого порядка.
Следующим шагом вводим замену переменных z=y/x, y=z*x, о которой постоянно будем напоминать, чтобы Вы ее заучили
![]()
После этого ДУ записываем в дифференциалах
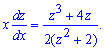
Далее преобразуем зависимость к дифференциальному уравнению с отделенными переменными
![]()
и интегрированием решаем его.
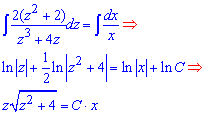
Интегралы несложные, остальные преобразования выполнены на основе свойств логарифма. Последнее действие включает экспонирования логарифма. Наконец возвращаемся к исходной замене и записываем решение дифференциального уравнения в форме
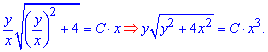
Константа "C" принимает любое значение. Все кто учится заочно имеют проблемы на экзаменах с данным типом уравнений, поэтому просьба внимательно посмотреть и запомнить схему вычислений.
Пример 3. Решить дифференциальное уравнение
![]()
Решение:Как следует из приведенной выше методики, дифференциальные уравнения такого типа решают методом введения новой переменной. Перепишем зависимость так, чтобы производная была без переменной
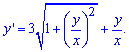
Далее по анализу правой части видим, что везде присутствует частка -ее и обозначаем за новую неизвестную
z=y/x, y=z*x.
Находим производную от y
![]()
С учетом замены первоначальное ДУ перепишем в виде
![]()
Одинаковые слагаемые упрощаем, а все получившие сводим к ДУ с отделенными переменными
![]()
Интегрированием обеих частей равенства
![]()
приходим к решению в виде логарифмов
![]()
Экспонируя зависимости находим общее решение дифференциального уравнения
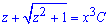
которое после подстановки в него начальной замены переменных примет вид
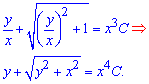
Здесь С - постоянная, которую можно доопределить из условия Коши. Если не задана задача Коши то стала принимает произвольное действительное значение.
Вот и вся мудрость в исчислении однородных дифференциальных уравнений.
Однако схема вычислений достаточно хорошо описана в книгах и дает возможность найти решение ДУ первого порядка, хоть при этом приходится выполнять массу вычислений. Чтобы не пугать Вас теорией сразу перейдем к анализу готовых ответов из которых все станет ясно.
Пример 1 Решить дифференциальное уравнение
![]() Решение:Перед нами совсем другой тип дифференциальных уравнений первого порядка чем те, что были рассмотрены ранее. Схема вычислений тоже отличается, сначала необходимо определить стационарную точку - для этого необходимо найти нули числителя и знаменателя.
Решение:Перед нами совсем другой тип дифференциальных уравнений первого порядка чем те, что были рассмотрены ранее. Схема вычислений тоже отличается, сначала необходимо определить стационарную точку - для этого необходимо найти нули числителя и знаменателя.
Составим и решим систему уравнений:
![]()
Стационарной точкой является М(-1;1).
Далее выполняем замену переменных (смещение координат)
![]()
отсюда исходное ДУ превратим до однородного дифференциального уравнения
![]() или
или ![]()
Выполним замену переменных 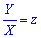 и найдем дифференциал через новую переменную
и найдем дифференциал через новую переменную
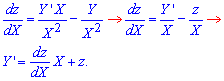
Подставляя в уравнение, получим простую для вычислений зависимость
![]()
которую легко сводим к уравнению с разделенными переменными
![]()
Далее интегрируем обе части
![]()
и находим общее решение уравнения
![]()
Возвращаясь к самой первой замене получим
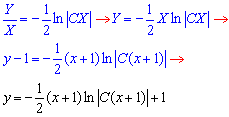
где 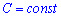 - произвольная константа.
- произвольная константа.
Вот в таком виде получили решение дифференциального уравнения. Хорошо разберите приведенную схему вычислений, она для студентов на цену золота.
Пример 2 Найти общий интеграл уравнения
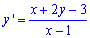 Решение:Данное дифференциальное уравнение первого порядка имеет достаточно простое решение, однако не каждый студент без шпаргалки или методички может найти ответ самостоятельно.
Решение:Данное дифференциальное уравнение первого порядка имеет достаточно простое решение, однако не каждый студент без шпаргалки или методички может найти ответ самостоятельно.
Методика сведения уравнения к однородному ДУ заключается в следующих действиях: находим особую точку (нули числителя и знаменателя дроби).
Для этого решаем систему линейных уравнений
![]()
Далее вводим замену переменных
![]()
Единицы справа являются решениями системы уравнений.
Наше первоначальное дифференциальное уравнение в новых переменных будет иметь запись
![]()
Именно для упрощения и решали систему уравнений.
Далее необходимо выполнить замену переменных
![]() тогда
тогда ![]()
После замены полученное ДУ можем свести к уравнению с разделенными переменными
![]()
Проинтегрировав обе части формулы
![]()
сначала придем к логарифмам
![]()
Далее экспонированием обеих частей получим зависимость вида
![]()
Возвращаясь к начальной замене переменных, получим решение ДУ в новых переменных
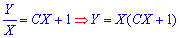
а дальше окончательный интеграл дифференциального уравнения
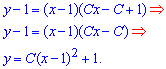
Здесь С=const- произвольная действительная константа, которая может бить определена из условия Коши.
Вот так сложно бывает иногда получить общее решение дифференциального уравнения.
Пример 3 Решить дифференциальное уравнение
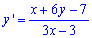 Решение:Имеем ДУ первого порядка оторое можем свести к однородному дифференциальному уравнению. Для этого составим систему уравнений из условия равенства нулю числителя и знаменателя дроби
Решение:Имеем ДУ первого порядка оторое можем свести к однородному дифференциальному уравнению. Для этого составим систему уравнений из условия равенства нулю числителя и знаменателя дроби
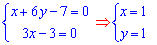
Зная координаты точки, выполняем перенос системы координат
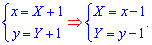
Исходное дифференциальное уравнение при этом преобразуется к виду
![]() или
или ![]()
Далее следует сделать замену переменных z=Y/X, Y=z*X, при этом производная равна
![]()
Подставим ее в уравнение и разделим переменные, так получим ДУ с разделенными переменными
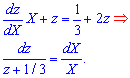
Интегрируя дифференциальное уравнение приходим к логарифмическому
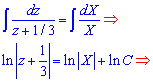
Далее экспонируем полученную зависимость, предварительно сведя логарифмы в правой части по формуле произведения
![]()
Возвращаясь к замене переменных (z) получим решение
![]()
которое после повторной замены приобретет понятный вид
![]()
Перенеся единицу вправо
![]()
получим общий интеграл дифференциального уравнения.
Здесь разобраны только 3 примеры, однако схему вычислений они описывают в полной мере. Теперь Вы знаете, что делать с уравнениями сводными к однородным и после самостоятельной работы с подобными примерами не будете иметь трудностей на контрольных и экзаменах. В следующем уроке Вас ждет еще масса готовых ответов для изучения других дифференциальных уравнений первого порядка и схем решения.
Пример 1. Найти решение задачи Коши для дифференциального уравнения
![]() Решение: Имеем неоднородное дифференциальное уравнение первого порядка. Как поступать с такими уравнениями подробно рассмотрены на предыдущих уроках.
Решение: Имеем неоднородное дифференциальное уравнение первого порядка. Как поступать с такими уравнениями подробно рассмотрены на предыдущих уроках.
Найдем сначала решение однородного ДУ. Интегрируем для этого уравнения (левую часть), предварительно разделив переменные:
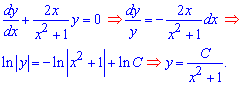
Далее считаем, что стала С(х) является функцией от переменной x
![]()
Все это делается для того, чтобы подобрать постоянную таким образом, чтобы удовлетворить неоднородную функцию - правая часть ДУ.
Найдем производную y' с учетом выше сказанного
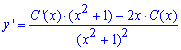
Подставляем функцию и ее производную в исходное дифференциальное уравнение
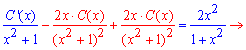
Видим, что двое слагаемых при суммировании дадут ноль и в результате получим зависимость для производной от постоянной
![]()
Из последнего уравнения методом интегрирования находим явный вид постоянной С(x)
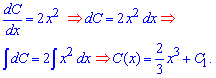
После этого можем записать общее решение уравнения
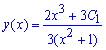
Но это еще не финал вычислений, нам нужно найти частичный решение (задача Коши). Для этого удовлетворяем начальное условие на функцию и вычисляем постоянную
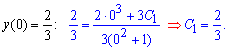
Итак, задача Коши решена и найдено частичное решение дифференциального уравнения в виде
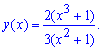
На этом одно из уравнений вычислено. Схема нахождения функции не слишком запутана с одной стороны, с другой ее легко реализовать (постоянную принимаем за функцию). Рассмотрим еще несколько готовых примеров, а дальше учитесь вычислять самостоятельно.
Пример 2. Решить задачу Коши для уравнения
![]() Решение:Имеем неоднородное дифференциальное уравнение первого порядка + условие Коши. Запишем и проинтегрируем соответствующее однородное уравнение, предварительно разделив переменные
Решение:Имеем неоднородное дифференциальное уравнение первого порядка + условие Коши. Запишем и проинтегрируем соответствующее однородное уравнение, предварительно разделив переменные
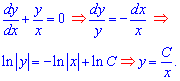
Решение однородного уравнения найти в данном случае довольно легко. Изучите для практики внесения сталой в интегралах под логарифм - это значительно упростит дальнейшие преобразования с решением. Далее рассмотрим константу C как функцию от переменной x
![]()
Производная y' по формуле примет выражение
![]()
Подставим функцию y и ее производную y' в исходное дифференциальное уравнение и выразим производную постоянной
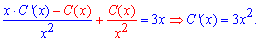
Интегрированием находим недостающую зависимость C(x)
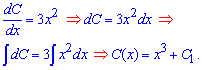
Заменив постоянную полученным только что значением, получим общее решение дифференциального уравнения
![]()
Решим задачу Коши. С начального условия имеем
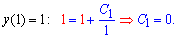
Определив сталую получим y=x2 - частичное решение дифференциального уравнения.
Пример 3. Найти решение дифференциального уравнения и задачи Коши
![]() Решение:Начнем с анализа левой части дифференциального уравнения. Интегрируем однородное дифференциальное уравнение, предварительно отделив в нем переменные
Решение:Начнем с анализа левой части дифференциального уравнения. Интегрируем однородное дифференциальное уравнение, предварительно отделив в нем переменные
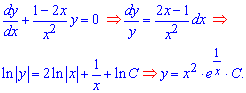
Для последнего перехода использовали свойство экспоненты - второе слагаемое записали как логарифм от экспоненты ln(exp(1/x)).
Теперь предположим, что константа C(x) - это функция от переменной x:
![]()
тогда ее производная равна
![]()
Подставляем постоянную и ее производную в исходное дифференциальное уравнение
![]()
которое после сокращения слагаемых превратится в зависимость
![]()
Из последнего уравнения функцию C(x) находим интегрированием
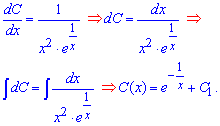
Итак, мы нашли общее решение дифференциального уравнения
![]()
Найдем частичное решение уравнения (задача Коши). Удовлетворим начальное условие на функцию и вычислим постоянную
![]()
Отсюда имеем y=x2 - частичное решение уравнения. На вид простая запись, хотя на ее вычисления потрачено немало времени.
Частичное решения двух последних примеров совпадают, такое редко бывает на практике. Теперь Вы знаете, как решить неоднородное уравнение и выполнить условие Коши.
Если на экзамене или контрольной работе Вам нужна помощь - обращайтесь. Мы помогли не одной тысячи студентов, сможем помочь и Вам.
Линейным дифференциальным уравнением первого порядканазывается уравнение вида y'+p(x)*y=g(x), где p(x) и g(x) – непрерывные на определенном промежутке функции.
Алгоритм метода Бернулли
1. Решение линейного дифференциального уравнения необходимо представить в виде произведения двух неизвестных функций y=u*v от аргумента u=u(x),v=v(x). Одну из этих функций можно выбрать произвольно, а вторая определяется из дифференциального уравнения.
2. По правилу производная произведения равна y=u*v,то y'=u'v+uv'.
3. Подставим запись функции y=u*v и производной y'=u'v+uv' в уравнение y'+p(x)*y=g(x) и получим u'v+uv'+p(x)*u*v= g(x). Сгруппируем второй и третий слагаемые, вынеся общий множитель (u) за скобки и придем к диф. уравнению u'v+u(v'+p(x)*v)=g(x).
4. Сперва определяем частное решение v=v(x), для этого решаем диф. уравнения v'+p(x)*v=0 и за произвольную постоянную интегрирования берем ноль (С=0). Данное уравнение является дифференциальным уравнением с разделяющимися переменными.
5. Далее подставим найденную функцию v=v(x) в исходное диф. уравнение u'v+uv'+p(x)*u*v= g(x), которое при этом упростится до вида u'v+u*0=g(x), то есть к дифференциальному уравнению с разделяющимися переменными u'v(х)=g(x) относительно u(x). Из этого уравнения находим u=u(x)+С.
6. Имея u=u(x) и v=v(x) находим общее решение ДУ через произведение y=u*v=( u(x)+С)* v(x).
7. Если задана задача Коши то с дополнительной условия на решение y(x0)=y0 определяем сталую С.
Пример 1. Найти решение задачи Коши
![]() Решение:Имеем неоднородное дифференциальное уравнение первого порядка. Запишем его в правильном виде, для этого перенесем в правую сторону функцию
Решение:Имеем неоднородное дифференциальное уравнение первого порядка. Запишем его в правильном виде, для этого перенесем в правую сторону функцию
![]()
Далее по схеме Бернулли делаем замену переменных y=u*v, y'=u'v+uv', где u=u(x) і v=v(x).
Учитывая что множители в левой части уровне
![]() и y2=u2v2
и y2=u2v2
получим следующее уравнение
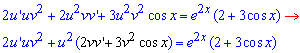
Согласно алгоритму Бернулли уравнение разделим на 2, для этого дужку слева (выделена черным) приравняем к нулю
![]()
Сводим к дифференциальному уравнению с разделенными переменными
![]()
и решаем интегрированием
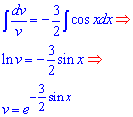
В результате получили экспоненту с отрицательным показателем синуса. При этом исходное дифференциальное уравнение достаточно упростится для поиска второй неизвестной пока функции
![]()
Перенесем экспоненту с отрицательным показателем в правую сторону
![]()
и сведем к ДУ с разделенными переменными
![]()
Интегрированием уравнения в дифференциалах
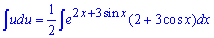
находим решение дифференциального уравнения
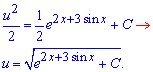
Как описано в начале, общее решение дифференциального уравнения равно произведению функций
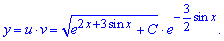
Но это еще не конечная ответ к задаче. Найдем частичное решение дифференциального уравнения (задача Коши), для этого определим постоянную с начального условия на функцию
![]()
Сталая равна нулю, это позволяет упростить формулу решения диф. уравнения, хотя мало кто из Вас увидит эту подсказку
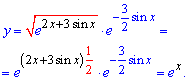
Мы нашли частичный решение дифференциального уравнения и он равен экспоненте в степени "икс" y=ex.
Пример 2. Решить дифференциальное уравнение та задачу Коши
![]() Решение:Задано неоднородное дифференциальное уравнение первого порядка, которое перепишем в виде
Решение:Задано неоднородное дифференциальное уравнение первого порядка, которое перепишем в виде
![]()
Выполняем замену переменных в уравнении
![]() , где "у" и "в" принимают функциональные зависимости
, где "у" и "в" принимают функциональные зависимости 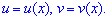
Находим выражения которые фигурируют в записи
![]()
и подставляем в исходное дифференциальное уравнение
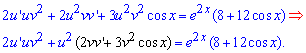
Далее схема вычислений заключается в разделении переменных. По алгоритму Бернулли выражение, содержащее "v" приравняем к нулю
![]()
Записываем уравнение в дифференциалах
![]()
Видим что имеем уравнение с разделяющимися переменным, поетому целесообразно разделить переменные
![]()
Проинтегрировав обе части
![]()
получим логарифм и синус.
![]()
Далее экспонируем обе части и таким образом находим одну из неизвестных функций
![]()
Исходное дифференциальное уравнение при этом упростится к виду
![]()
Экспоненту в отрицательном показателе переносим вправо от знака равенства
![]()
Далее распишем уравнения через дифференциалы (/2)
![]()
и сведем к уравнению с разделенными переменными
![]()
Интеграл в правой части выглядит тяжелым для высчисления, но если внести дужку под дифференциал, то получим показатель экспоненты
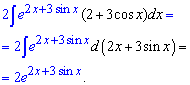
Окончательно после интегрирования получим
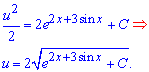
Общий интеграл дифференциального уравнения записываем через произведение функций
![]()
Чтобы найти частичное решение дифференциального уравнения (задачи Коши) используем начальное условие
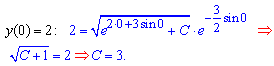
Из него определим постоянную и подставим в уравнение частного решения дифференциального уравнения
![]()
На этом и построен алгоритм Бернулли вычислений дифференциальных уравнений такого типа. Используйте алгоритм решения уравнения Бернулли ко всем подобным дифференциальным уравнениям.
Далее разбор готовых примеров, после которого возможно у Вас не останется вопросов по данной теме.
Уравнение в полных дифференциалах
Определение 1. Уравнение вида M(x,y)dx+N(x,y)dx=0 называется уравнением в полных дифференциалах, если зависимость перед знаком равенства является полным дифференциалом некоторой функции двух переменных u(x,y), то есть справедливая формула
du(x,y)=M(x,y)dx+N(x,y)dx. (1)
Таким образом, первоначальное уравнение по содержанию означает равенство нулю полного дифференциала функции
du(x,y)=0.
Интегрируя дифференциал получим общий интеграл ДУ в виде
u(x,y)=С. (2)
При вычислениях, как правило, постоянную возлагают равной нулю.
Пред вычислениями всегда возникает вопрос "Как проверить что заданное ДУ является уравнением в полных дифференциалах?"
На этот вопрос дает ответ следующее условие.
Необходимое и достаточное условие полного дифференциала
Необходимым и достаточным условием полного дифференциала является равенство между собой частных производных
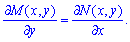 (3)
(3)
При решении дифференциальных уравнений его проверяют в первую очередь, чтобы идентифицировать имеем ли уравнение в полных дифференциалах или возможно другое.
По содержанию это условие означает что смешанные производные функции равны между собой.
В формулах учитывая зависимости
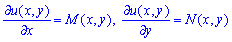 (4)
(4)
необходимое и достаточное условие существования полного дифференциала можем записать в виде
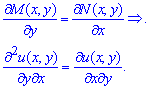
Приведенный критерий и применяют при проверке уравнения на соответствие полному дифференциалу, хотя при изучении данной темы преподаватели не зададут Вам другого типа уравнений.
Алгоритм решения уравнения в полных дифференциалах
С обозначений (4) частных производных полного дифференциала функции следует, что u(x,y) мы можем найти интегрированием
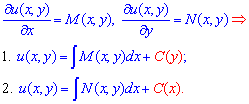
Эти формулы дают выбор при вычислениях, поэтому для интегрирования выбирают ту частную производную, интеграл от которой легче найти на практике.
Далее второй важный момент - неопределенный интеграл представляет собой первообразную то есть "+ С", которую следует определить.
Поэтому, если интегрируем частную производную M(x,y) по "икс" то сталая зависит от y и наоборот - если интегрируем N(x,y) по y то сталая зависима от "икс".
Далее чтобы определить постоянную берут производную от u(x,y ) по другой переменной чем та, по которой производили интегрирование и приравнивают к второй частичной производной.
В формулах это будет выглядеть следующим образом
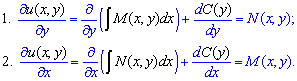
Как правило некоторые слагаемые упрощаются и получим уравнение на производную постоянной. Для первого из уравнений получим
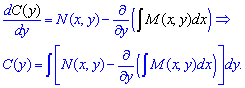
Окончательно общий интеграл после определения постоянной имеет вид
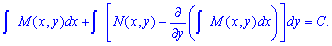
В симметричной форме получим ответ и для другого уравнения.
Запись только на вид сложная, на самом деле на практике все выглядит значительно проще и понятнее. Проанализируйте следующие задачи на полные дифференциалы.
Готовые ответы на уравнение в полных дифференциалах
Пример 1. Решить дифференциальное уравнение
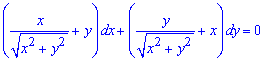
Решение:Левая часть уравнения является полным дифференциалом некоторой функции 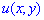 , поскольку выполняется условие
, поскольку выполняется условие
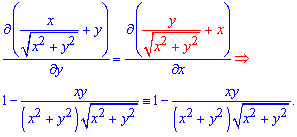
Отсюда записываем частную производную функции двух переменных от "икс"
![]()
и интегрированием находим ее вид
![]()
Чтобы доопределить постоянную находим частную производную функции по "y" и приравниваем со значением в уравнении
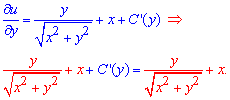
Подобные слагаемые в правой и левой части сокращаем, после чего постоянную находим интегрированием
![]()
Теперь имеем все величины для записи общего решения дифференциального уравнения в виде
![]()
Как можно убедиться, схема решения уравнений в полных дифференциалах не сложная и ее под силу выучить каждому. Важное значение имеют множители при дифференциалах, поскольку их приходится интегрировать и дифференцировать чтобы найти решение.
Пример 2. (6.18) Найти интеграл дифференциального уравнения
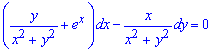
Решение: По теории левая часть уравнения должна быть полным дифференциалом некоторой функции двух переменных u(x,y), при этом проверяем выполняется ли условие
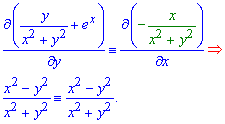
Отсюда берем частную производную и через интеграл находим функцию
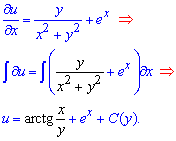
Вычисляем частную производную функции двух переменных по y и приравниваем к правой стороне дифференциального уравнения.
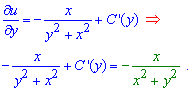
Производная выражается зависимостью
![]()
С учетом постоянной получили общий интеграл дифференциального уравнения в виде
![]()
На этом вычисления данного примера завершено.
Пример 3. (6.20) Решить дифференциальное уравнение
![]()
Решение: Левая часть уравнения будет полным дифференциалом некоторой функции двух переменных u(x; y) , если будет выполняться условие
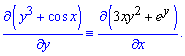
Отсюда начинаем решать уравнения, а вернее интегрирование одной из частных производных
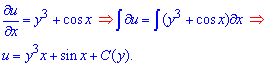
Далее находим производную от полученной функции по переменной y и приравниваем к правой стороне дифференциальной зависимости
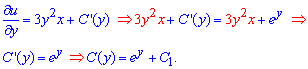
Это позволяет найти константу, как функцию от y. Если начинать раскрывать дифференциальную зависимость с правой стороны, то получим что константа зависит от x. Общее решение дифференциального уравнения при этом не изменится и для заданного уравнения имеет вид
![]()
На этом пример решен.
Пример 4. (6.21) Решить дифференциальное уравнение
![]()
Решение: Проверяем является ли полным дифференциалом некоторой функции u(x,y) выражение в левой стороне уравнения
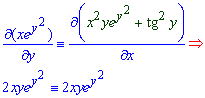
Выписываем частную производную функции двух переменных и интегрированием восстанавливаем решение
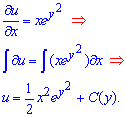
Далее уточняем постоянную. Для этого вычисляем производную функции по y и приравниваем к значению в уравнении (выделено зеленым)
![]()
![]()
Отсюда, выражаем производную и интегрируем
![]()
Общее решение дифференциального уравнения можем записать формулой
![]()
Для закрепления тематики просим самостоятельно проверить что данные уравнения являются уравнениями в полных дифференциалах и решить их:
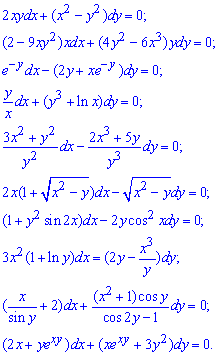 Здесь Вам и корневые функции, тригонометрические, экспоненты, логарифмы, одним словом - все что может ожидать Вас на модулях и экзаменах.
Здесь Вам и корневые функции, тригонометрические, экспоненты, логарифмы, одним словом - все что может ожидать Вас на модулях и экзаменах.
После этого Вам станет гораздо проще решать такого типа уравнения.
Из следующей статьи Вы познакомитесь с уравнениями вида
M(x,y)dx+N(x,y)dx=0
которые достаточно подобные уравнению в полных дифференциалах, однако в них не выполняется условие равенства частных производных. Их вычисляют поиском интегрирующего множителя, умножая на который приведенное уравнение становится уравнением в полных дифференциалах.
M(x,y)dx + N(x,y)dy = 0)
левая часть которого является полным дифференциалом некоторой функции
U(x,y), то есть dU(x,y) = M(x,y)dx + N(x,y)dy.
Напомним, что полный диференциал функции U находится по формуле
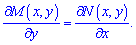 (1)
(1)
Уравнение сводные к ДР в полных дифференциалах
В некоторых случаях зависимость
M(x,y)dx + N(x,y)dy = 0
не является уравнением в полных дифференциалах, не выполняется условие (1). Однако существует функция "мю" 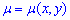 такова, что если на нее умножить первоначальное уравнение
такова, что если на нее умножить первоначальное уравнение ![]() то получим уравнением в полных дифференциалах.
то получим уравнением в полных дифференциалах.
Необходимым и достаточным условием этого является равенство между собой частных производных
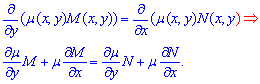
Функция "мю" называют интегрирующим множителем.
Таким образом кроме ДУ относительно функции u(x,y) на практике приходится решать дифференциальное уравнение в частных производных относительно интегрирующего множителя.
Но до сих пор остается открытым вопрос, как искать интегрирующий множитель?
Как найти интегрирующий множитель?
В теории обычно методика уже разработана и интегрирующий множитель следует искать в виде
![]() где "омега"
где "омега" ![]() - известная функция одной или двоих переменных.
- известная функция одной или двоих переменных.
В этом случае получаем
![]() После подстановки в условие полного дифференциала получим
После подстановки в условие полного дифференциала получим
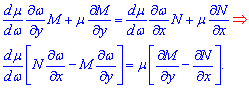 Разделим переменные в последней строке
Разделим переменные в последней строке
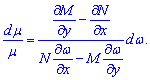 Проинтегрировав и положив постоянную интегрирования равной нулю находим интегрирующий множитель
Проинтегрировав и положив постоянную интегрирования равной нулю находим интегрирующий множитель
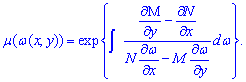 Рассмотрим частные случаи.
Рассмотрим частные случаи.
1) Пусть "омега" равна аргументу. Тогда некоторые частные производные равны нулю, а интегрирующий множитель находят по формуле
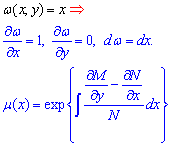 2) Если "омега" ровна y то формула вычисления интегрирующего множителя имеет вид
2) Если "омега" ровна y то формула вычисления интегрирующего множителя имеет вид
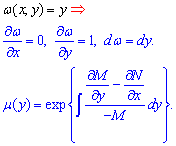 3) В случае когда "омега" равна сумме или разности квадратов переменных интегрирующий множитель находим по формуле
3) В случае когда "омега" равна сумме или разности квадратов переменных интегрирующий множитель находим по формуле
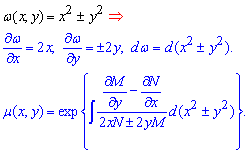 4) И вариант когда имеем произведение переменных дает следующую зависимость для определения мю
4) И вариант когда имеем произведение переменных дает следующую зависимость для определения мю
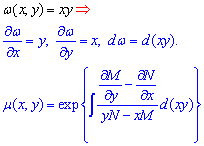 Вывод формулы интегрирующего множителя без практики Вас ничего не научит, поэтому рассмотрим задачи из контрольной работы на которых Вы увидите суть всех приведенных выше формул. Примеры задавали во Львовском национальном университете им. И. Франка .
Вывод формулы интегрирующего множителя без практики Вас ничего не научит, поэтому рассмотрим задачи из контрольной работы на которых Вы увидите суть всех приведенных выше формул. Примеры задавали во Львовском национальном университете им. И. Франка .
Уравнение в полных дифференциалах. Задача Коши.
Пример 1. Решить дифференциальное уравнение и задачу Коши
![]() Решение: Выпишем множители при дифференциалах
Решение: Выпишем множители при дифференциалах
![]()
и проверим выполняется ли условие полного дифференциала функции двух переменных
![]()
Как видим, левая часть уравнения не является полным дифференциалом (условие не выполняется). Проверим допускает ли дифференциальное уравнение интегрирующий множитель
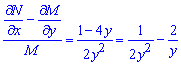
С правой стороны видим, что данное уравнение допускает множитель интегрирования, причем он зависит только от y.
Найдем интегрирующий множитель из дифференциального уравнения с отделенными переменными
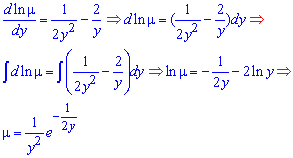
После умножения всех членов уравнения на найденный интегрирующий множитель "мю" (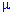 ) получим Ду первого порядка
) получим Ду первого порядка
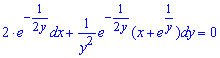
Если вновь проверить ДУ, то тепер условие на полный дифференциал некоторой функции выполняется
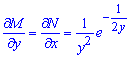
Далее будем решать полученное ДУ, как в случае обычного полного дифференциала. Проинтегрируем второе слагаемое по y
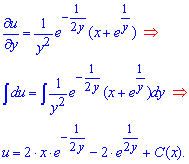
Запомните правило - если интегрирования идет по y, то сталая зависит от "икса", и наоборот.
Сталую которая входит в уравнения определяют вычислением частичной производной найденного решение по "икс" и приравниванием до множителя в ДУ при dx.
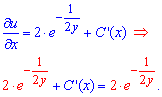
Отсюда находим постоянную
![]()
Учитывая все вышеизложенное, записываем общий интеграл дифференциального уравнения
![]()
В задании необходимо найти частичное решение (задачу Коши). Для этого записываем дополнительное условие на функцию и определяем сталую
![]()
Отсюда имеем частичное решение дифференциального уравнения
![]()
Оно пока записано в неявной форме, однако в этом случае можем найти зависимость функции от переменной y(x):
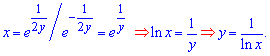 - частичное решение дифференциального уравнения.
- частичное решение дифференциального уравнения.
Пример 2.Найти решение задачи Коши
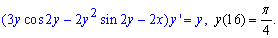 Решение: Записываем заданное дифференциальное уравнение первого порядка в дифференциалах
Решение: Записываем заданное дифференциальное уравнение первого порядка в дифференциалах
![]()
Далее проверим имеем ли полный дифференциал, выписываем множители
![]()
и находим частные производные
![]()
Условие на полный дифференциал не выполняется.
Проверим не допускает это уравнение интегрирующего множителя
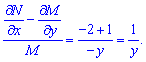
Видим что данное уравнение допускает интегрирующий множитель который зависит только от y. Найдем его интегрированием уравнения
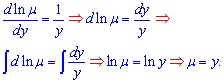
После умножения всех членов уравнения на найденный интегрирующий множитель исходное ДУ преобразуется к виду
![]()
что соответствует уравнению в полных дифференциалах
![]()
Как решить такое уравнение Вы уже знаете, поэтому переходим к интегрированию для простоты второго доданка (возле dx)
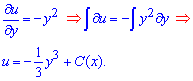
Чтобы определить постоянную - ищем частную производную функции u по "икс" и приравниваем ко второму множителя в полном дифференциале
![]()
На этот раз сталая функции не ровна константе и для ее установки нужно найти несколько интегралов
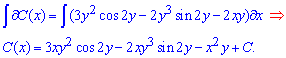
Общий интеграл дифференциального уравнения при подстановке C(x) примет вид
![]()
Решим задачу Коши для ДУ
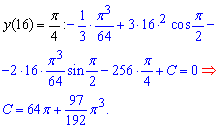
Отсюда имеем
![]() - частичное решение дифференциального уравнения.
- частичное решение дифференциального уравнения.
Пример 3. Найти решение уравнения при условии Коши
![]() Решение: Перепишем ДУ расписав производную дифференциалами
Решение: Перепишем ДУ расписав производную дифференциалами
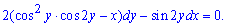
Далее действуем по методике для таких уравнений.
Выписываем множители возле дифференциалов
![]()
Проверяем условие на полный дифференциал функции
![]()
Условие не выполняется. Проверим, допускает ли интегрирующий множитель данное уравнение ?
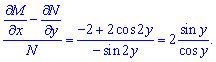
Как видим правая сторона зависима от y поэтому уравнение допускает интегрирующий множитель.
Найдем его из ДУ
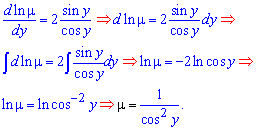
После умножения всех членов уравнения на интегрирующий множитель "мю" получим следующее уравнение
![]()
Условие полного дифференциала подтверждается
(![]() ).
).
Далее применяем методику для ДУ в полных дифференциалах. С первого слагаемого уравнения интегрированием находим зависимость u(y)
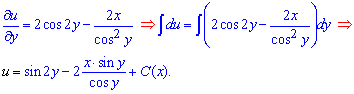
Далее вычисляем частную производную функции u(x,y) по "икс"
![]()
и сравниваем с частичной производной начального уравнения
![]()
Нетрудно найти отсюда константу
![]()
Возвращаемся и записываем общий интеграл дифференциального уравнения
![]()
По условию необходимо найти частичный интеграл уравнения (решить задачу Коши). Для этогоопределяем значение функции в точке
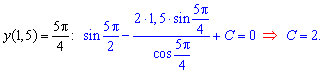
Константа равна 2, а частичное решение ДУ
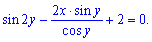
Для ясности ответа найдем (обратную) зависимость х(у):
![]() - частичное решение уравнения
- частичное решение уравнения
Красивый ответ несмотря на массу преобразований и интегралов.
Из приведенных ответов Вы получили полезную инструкцию для вычислений. Для проверки полученных знаний самостоятельно найдите решение уравнений, используя интегрирующий множитель
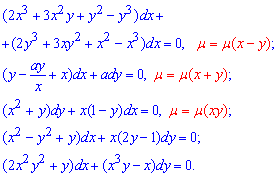 Оставайтесь с нами, впереди еще много готовых примеров дифференциальных уравнений.
Оставайтесь с нами, впереди еще много готовых примеров дифференциальных уравнений.
Пример 1. Решить дифференциальное уравнение
тогда третья производная функции равна
Исходное однородное ДУ упростится к виду
Записываем его в дифференциалах, далее сводим к уравнению с разделенными переменными и находим решение интегрированием
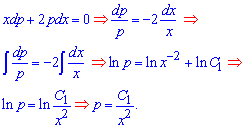
Вспоминаем что параметр это вторая производная функции
поэтому для нахождения формулы самой функции дважды интегрируем найденную дифференциальную зависимость
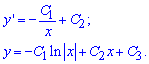
В функции сталые C1, C2, C3 – равны произвольным значениям.
Вот так просто выглядит схема позволяющая найти общее решение однородного дифференциального уравнения методом введения параметра. Следующие задачи более сложные и из них вы научитесь решать неоднородные дифференциальные уравнения третьего порядка. Между однородными и неоднородными ДУ в плане вычислений является некоторое различие, в этом Вы сейчас убедитесь.
Пример 2.Найти общее решение дифференциального уравнения
![]() Решение:Имеем неоднородное дифференциальное уравнение третьего порядка. Поэтому его решение следует искать в вид суммы двух - решения однородного и частного решения неоднородного уравнения
Решение:Имеем неоднородное дифференциальное уравнение третьего порядка. Поэтому его решение следует искать в вид суммы двух - решения однородного и частного решения неоднородного уравнения
![]()
Решим сначала однородное дифференциальное уравнение
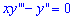
Как видите оно содержит только вторую и третью производную функции и не содержит самой функции. Такого сорта диф. уравнения решают методом введения параметра, что в в свою очередь снижает и упрощает нахождение решения уравнения. На практике это выглядит следующим образом: пусть вторая производная равна определенной функции ![]() , тогда третья производная формально будет иметь запись
, тогда третья производная формально будет иметь запись
![]()
Рассмотренное однородное ДУ 3 порядка преобразуется к уравнению первого порядка
![]()
откуда разделяя переменные находим интеграл
x*dp-p*dx=0;
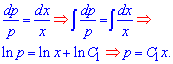
Сталые в таких задачах рекомендуем нумеровать, поскольку решение дифференциального уравнения 3 порядка имеет 3 постоянные, четвертого - 4 и и дальше по аналогии. Теперь возвращаемся к введенному параметру: поскольку вторая производная имеет вид ![]() то интегрируя ее один раз мы имеем зависимость для производной функции
то интегрируя ее один раз мы имеем зависимость для производной функции
![]()
и повторным интегрированием находим общий вид однородной функции
![]()
Частичное решение уравнения запишем в виде переменной умноженной на логарифм. Это следует из того что правая (неоднородная) часть ДУ равна -1/x и чтобы получить эквивалентную запись
![]()
следует решение искать в виде
![]()
Найдем коэффициент A, для этого вычислим производные первого и второго порядков
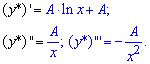
Подставим найденные выражения в исходное дифференциальное уравнение и приравняем коэффициенты при одинаковых степенях x:
![]()
Сталая равна -1/2, а решение неоднородного уравнения имеет вид
![]()
Общее решение дифференциального уравнения записываем в виде суммы найденных
![]()
где C1, C2, C3- произвольные константы которые можно уточнить с задачи Коши.
Пример 3. Найти интеграл ДУ третьего порядка
![]() Решение:Ищем общий интеграл неоднородного ДУ третьего порядка в виде суммы решения однородного и частичного неоднородного уравнения
Решение:Ищем общий интеграл неоднородного ДУ третьего порядка в виде суммы решения однородного и частичного неоднородного уравнения ![]() . Сначала для любого типа уравнений начинаем анализировать однородное дифференциальное уравнение
. Сначала для любого типа уравнений начинаем анализировать однородное дифференциальное уравнение
![]()
Оно содержит только вторую и третью производные неизвестной пока функции. Вводим замену переменных (параметр): обозначим за вторую производную
![]()
Тогда третья производная равна
![]()
Такие же преобразования выполняли в предыдущем задании. Это позволяет свести дифференциальное уравнения третьего порядка к уравнению первого порядка вида
![]()
Интегрированием находим решение однородного уравнения
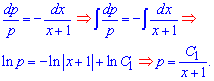
Вспоминаем, что в соответствии с заменой переменных это всего лишь вторая производная
![]()
а чтобы найти решение однородного дифференциального уравнения третьего порядка ее нужно дважды проинтегрировать
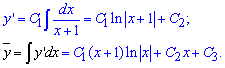
Исходя из вида правой стороны (неоднородной части =x+1), частичное решение уравнения ищем в виде
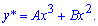
Как знать в каком виде искать частичный решение Вас должны были научить в теоретической части курса дифференциальных уравнений. Если нет, то можем только подсказать, что за функцию выбирают такое выражение чтобы при подстановке в уравнение слагаемое, содержащее старшую производную или моложе был одного порядка (подобный) с неоднородной частью уравнения
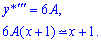
Думаю теперь Вам понятнее, откуда берется вид частного решения. Найдем коэффициенты A, B, для этого вычисляем вторую и третью производную функции
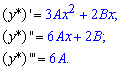
и подставляем в дифференциальное уравнение. После группировки подобных слагаемых получим линейное уравнение
![]()
из которого при одинаковых степенях переменной составляем систему уравнений
![]()
и находим неизвестные сталые. После их подстановки частичное решение уравнения выражается зависимостью
![]()
Общее решение дифференциального уравнения равно сумме однородного и частичного и имеет вид
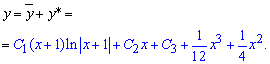
где С1, С2, С3 - произвольные константы.
Пример 4. Решить дифференциальное уравнение
![]() Решение:Имеем неоднородное дифференциальное уравнение третьего порядка решение которого будем находить через сумму
Решение:Имеем неоднородное дифференциальное уравнение третьего порядка решение которого будем находить через сумму ![]() . Схема вычислений Вам известна, поэтому переходим к рассмотрению однородного дифференциального уравнения
. Схема вычислений Вам известна, поэтому переходим к рассмотрению однородного дифференциального уравнения
![]()
По стандартной методике вводим параметр ![]()
Исходное дифференциальное уравнение примет вид 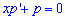 , откуда разделив переменные находим интеграл однородного уравнения
, откуда разделив переменные находим интеграл однородного уравнения
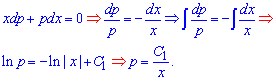
Вспоминаем что параметр равен второй производной ![]()
Интегрируя ДУ получим первую производную функции
![]()
Повторным интегрированием находим общий интеграл однородного дифференциального уравнения
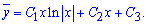
Частичное решение уравнения ищем в виде ![]() , так как правая часть равна
, так как правая часть равна ![]()
Найдем коэффициент A - для этого подставим y* в дифференциальное уравнение и приравняем коэффициент при одинаковых степенях переменной
![]()
После подстановки и группировки слагаемых получим зависимость
![]()
из которой сталая равна A=8/3.
Таким образом, можем записать частичное решение ДУ
![]()
Общее решение дифференциального уравнения равно сумме найденных
![]()
где С1, С2, С3 - произвольные константы. Если заданно условие Коши, то их очень легко можем доопределить.
Считаю, что материал Вам пригодится при подготовке к практическим занятиям, модулям или контрольной работе. Здесь не разбирали задачу Коши, однако из предыдущих уроков Вы в целом знаете как это сделать.
Пример 1. (9.17) Решить дифференциальное уравнение
Решение: Имеем неоднородное дифференциальное уравнение четвертого порядка. Вы должны знать что решение в таких уравнениях нужно представить в виде суммы интеграла однородного уравнения и частного решения неоднородного
Сначала всегда начинаем анализ с однородного дифференциального уравнения
Представим решение в вид экспоненты в степени y=ek*x.
Далее подставляем y в уравнение и, пренебрегая множителем exp(k*x) (он всегда больше нуля), выписываем характеристическое уравнение
Решив его получим следующие значения k1=0, k2=k3=k4=1.
Поскольку корни характеристического уравнения действительны числа, причем три из них одинаковые, то решение однородного уравнения представим в виде
Неоднородная часть заданного уравнения x-3 имеет вид полинома P(x)ex, причем коэффициент в показательной функции является корнем характеристического уравнения (k=0, откуда e0*x=1), поэтому частичный решение неоднородного уравнения ищем в виде
Найдем коэффициенты A и B: для этого подставим функцию в исходное дифференциальное уравнение и приравняем множители при одинаковых степенях переменной x
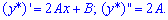
Третья и четвертая производные равны нулю
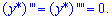
Подставляя в уравнение и группируя подобные выражения, получим
откуда составляем систему линейных уравнений
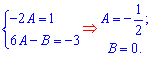
и находим сталые A=-1/2 и B=0.
Таким образом частичное решение неоднородного уравнения выражается формулой
Общее решение дифференциального уравнения равно сумме найденных функций
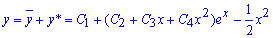
здесь С1-С4 - произвольные константы, которые можно уточнить если уравнение имеет условие Коши.
Пример 2. (9.23) Найти интеграл дифференциального уравнения![]()
Решение: Решение неоднородного дифференциального уравнения третьего порядка по приведенной выше схеме подаем через сумму
![]()
Сначала рассмотрим однородное дифференциальное уравнение![]()
Опуская промежуточные действия, которые описаны в 1 задании, записываем характеристическое уравнение и находим его корни
![]()
Так как корни характеристического уравнения различные, то решение записываем через сумму экспонент в соответственных степенях ![]()
Согласно правой части уравнения (x-1) частичное решение ищем в виде
![]()
Для определения коэффициентов A, B вычислим производные первого - третьего порядка 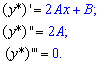
и подставим в исходное дифференциальное уравнение
![]()
Приравняв множители при одинаковых степенях переменной составляем систему линейных уравнений
![]()
из которой находим постоянные![]()
Теперь можем записать частичное решение дифференциального уравнения![]()
Общее решение дифференциального уравнения находим по формуле
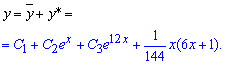
В нем присутствуют три константы, которые могут принимать произвольное значение. Доопределить их может только условие Коши, однако в задании оно не задано.
Пример 3.(9.12) Решить дифференциальное уравнение
![]()
Решение: Решение неоднородного дифференциального уравнения четвертого порядка ищем через сумму двух.
1. Для однородного дифференциального уравнения
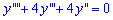
характеристическое уравнение после подстановки функции y=exp(k*x) будет иметь вид
![]()
Корни искать в большинстве случаев легко, например данное имеет решением ноль кратности 2, остальные два корня находим по теореме Виета с квадратного уравнения
k2-4k+4=0
В результате получим k1=k2=0 и k3=k4=-2. Поскольку корни характеристического уравнения действительны числа, причем каждые 2 из них одинаковые (кратные), то решение однородного дифференциального уравнения записываем в виде 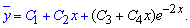
Неоднородная часть заданного уравнения x-x2 имеет вид полинома второго порядка P2(x), поэтому частичный решение ищем в виде
![]()
Найдем коэффициенты A, B и D : для этого функцию подставляем в исходное дифференциальное уравнение и приравниваем коэффициенты при одинаковых степенях x:
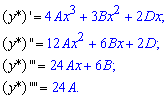
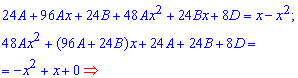
В результате придем к системе из 3 линейных уравнений
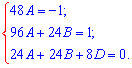
Мудрить здесь не приходится - имеем готовую схему Гаусса, поэтому последовательно с первого уравнения находим A, с второго - B, третьего - D
![]()
Подставляем найденные значения в формулу частного решения уравнения![]()
Общее решение дифференциального уравнения 4 порядка находим суммированием функций
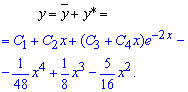
Сталые С1, С2, С3, С4 – принимают произвольные значения. Если задание содержит задачу Коши то их определяем с начального условия.
На этом знакомство с методикой вычисления дифференциальных уравнений через характеристическое уравнение завершено. Совершенствуйте умение дифференцировать и интегрировать и со временем подобные Ду для Вас также будут легкими.
А для этого нужно много работать самостоятельно, поэтому в качестве домашнего задания попробуйте найти решение следующих дифференциальных уравнений.