ЗНО математика. Системи показникових рівнянь

Шановні школярі, випускники, абітурієнти, цей розділ допоможе при підготовці до зовнішнього оцінювання 2017 року з математики. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці до тестування, систематизувати та підвищити накопичений рівень знань з математики.

Розділ II. Рівняння і нерівності

Завдання 11.72 Розв'яжіть систему показникових рівнянь

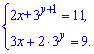
та знайдіть суму х0 + у0 для одержаного розв'язку (х0; у0) системи рівнянь.
Розв'язання: Маємо змішану систему рівнянь в якій міститься і показникове і лінійне рівняння. Щоб отримати лише показникові рівняння помножимо 1 з рівнянь на 3, а друге – на 2. В результаті отримаємо

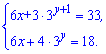
Від першого рівняння віднімемо друге

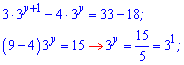
y=1 – одна з невідомих системи рівнянь. Підставимо її у друге рівняння та обчислимо другу невідому
3*x+2*3=9;
3*x=9-6=3;
x=3/3.
За умовою знаходимо суму розв'язків 1+1=2.
Відповідь: 2.

Завдання 11.73 (Т-06, 26) Розв'яжіть систему показникових рівнянь

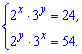
Запишіть у відповідь СУМУ х₀ + у₀, якщо пара (х₀; у₀) є розв'язком системи рівнянь.
Розв'язання: Дана система показникових рівнянь записана в такому вигляді, що виразити одну змінну (основу в степені змінної) з одного із рівнянь і підставити в друге рівняння не вдасться. Але методика розв'язання показникових систем рівнянь такого типу є. Вона полягає в тому, що для визначення зв'язку між змінними необхідно одне рівняння поділити на інше. З огляду на вигляд рівнянь розділимо 2 на 1, в результаті дістанемо

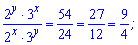
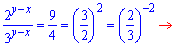
y-x=-2; y=x-2.
Наразі все Вам має бути зрозуміло. Далі підставимо знайдену залежність у будь-яке із рівнянь системи
2^x*3^x-2=24.
Розпишемо показники, щоб спростити

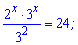
6^x=24*9=8*3*9=2³*3³=6³.
Прирівнюємо показники і знаходимо розв'язок системи рівнянь
x=3; y=3-2=1.
Залишилося обчислити суму знайдених значень
x+y=3+1=4.
Відповідь: 4.