ЗНО математика. Корені рівняння

Шановні школярі, випускники, абітурієнти, цей розділ допоможе при підготовці до зовнішнього оцінювання 2017 року з математики. Відповіді до тестів допоможуть Вам зрозуміти матеріал та методику обчислень при підготовці до тестування, систематизувати та підвищити накопичений рівень знань з математики.

Розділ II. Рівняння і нерівності

Завдання 11.62 Використовуючи графік функції f(х) = х³ - 27х знайдіть найменше ціле значення параметра а, при якому рівняння
х³-27х=а
має три різні корені.
Розв'язання: Дане завдання потребує визначення локальних екстремумів функції. Для цього обчислимо похідну функції та прирівняємо її до нуля
f''(х) = 3x^2 – 27;
f''(х) =0;
x^2-27/3=0;
х²= 27/3=9.
Звідси знаходимо точки екстремуму 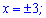та екстремальні значення функції
f'(3) = 3³ – 27*3=27*(1-3)=-27*2=-54 ;
f'(-3) =( -3)³ – 27*(-3)=-27+27*3=278(3-1) =54.
Графік функції на інтервалі, що включає локальні екстремуми функції наведено нижче

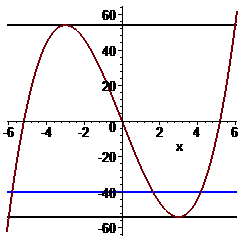
Якщо параметр належить інтервалу

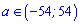
між локальними піками то пряма перетинає графік кубічної функції в 3 точках. Неважко перевірити, що параметр повинен дорівнювати
a=-53.
Відповідь: -53.

Завдання 11.63 Вкажіть кількість коренів рівняння

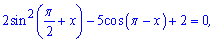
які задовольняють нерівність.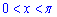
Розв'язання: Для початку задане тригонометричне рівняння слід спростити, бо в такому вигляді його можна обчислювати хіба що в математичних пакетах. Враховуючи періодичність синуса і косинуса перетворимо доданки, що входять в рівняння згідно приведених нижче формул

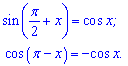
Після цього рівняння прийме зрозумілий вигляд

і бачимо, що заміною змінних t=cos(x) рівняння зведеться до квадратного
2t²+5t+2=0.
Таке рівняння відомо як розв'язувати, і для початку обчислимо дискримінант
D=25-4*2*2=25-16=9,
а далі корені рівняння

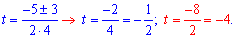
Другий корінь рівняння відкидаємо, оскільки косинус не може приймати таких значень. Перший корінь підставляємо в заміну і обчислюємо

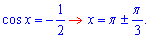
На проміжку

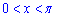
маємо тільки один розв'язок рівняння

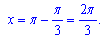
Відповідь: 1.