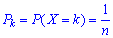 У табличній формі запису рівномірний закон розподілу має вигляд:
У табличній формі запису рівномірний закон розподілу має вигляд: Умова нормування для рівномірного закону розподілу має вигляд
Умова нормування для рівномірного закону розподілу має вигляд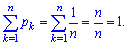 Імовірнісна твірна функція на основі першої формули приймає значення
Імовірнісна твірна функція на основі першої формули приймає значення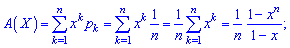
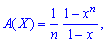 або
або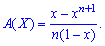 Числові характеристики рівномірного закону знаходимо на основі твірної функції
Числові характеристики рівномірного закону знаходимо на основі твірної функції
1. Математичне сподівання знаходимо за формулою
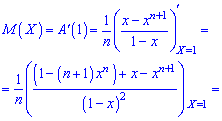
При х = 1 отримуємо невизначеність (0/0), яку розкриваємо за правилом Лопіталя
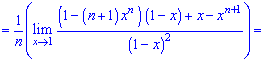
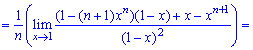
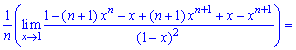
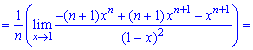
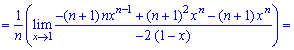
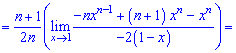
При х = 1 знову маємо невизначеність виду (0/0), яку також розкриваємо за правилом Лопіталя
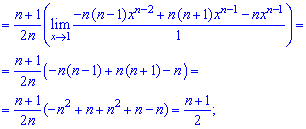
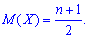 Обчислення зайняли багата часу, однак формула для математичного сподівання вийшла досить легкою.
Обчислення зайняли багата часу, однак формула для математичного сподівання вийшла досить легкою.
2. Виконавши подібні, але більш громіздкі перетворення, дисперсію і середнє математичне відхилення знаходимо за готовими формулами
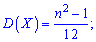
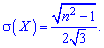
3. Для рівномірного розподілу ймовірностей асиметрія і ексцес рівні нулю
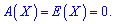
Є й інше означення, згідно з яким функція має рівномірний розподіл, якщо на деякому інтервалі щільність імовірностей приймає постійне значення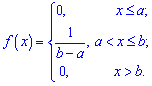 Функція розподілу ймовірностей для рівномірного закону визначається інтегруванням
Функція розподілу ймовірностей для рівномірного закону визначається інтегруванням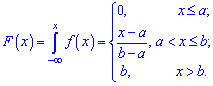 Математичне сподівання в таких випадках визначають залежністю
Математичне сподівання в таких випадках визначають залежністю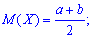 дисперсію за формулою
дисперсію за формулою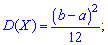 і середнє квадратичне відхилення через корінь
і середнє квадратичне відхилення через корінь Ймовірність влучання випадкової величини Х в деякий інтервал
Ймовірність влучання випадкової величини Х в деякий інтервал 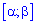 , який міститься всередині інтервалу
, який міститься всередині інтервалу 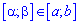 визначається за формулою
визначається за формулою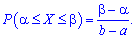 Наведені формули часто є більш застосовуваними на практиці ніж ті, що були дані вище.
Наведені формули часто є більш застосовуваними на практиці ніж ті, що були дані вище.
Розглянемо приклади відшукання числових характеристик.
Приклад 1. Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення М (Х), D (X), S (Х), якщо цілочислова випадкова величина Х має рівномірний закон розподілу і можливі значення її значення лежать в діапазоні 1..50:
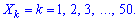 .
.
Розв'язання. За умовою задачі маємо такі дані n = 50, p = 1/50=0,02.
Згідно формул обчислюємо математичне сподівання
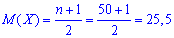
дисперсія
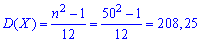
середнє квадратичне відхилення
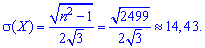
Приклад 2. Поїзда в метро прибувають на станцію кожні 10 хвилин. Визначити ймовірність того, що час очікування поїзда не буде більшим за 4 хвилини.
Розв'язання. За умовою задачі маємо два інтервали
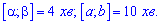
Згідно формули, шукана ймовірність рівна частці цих величин
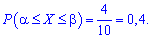
Задачі на відшукання інтервалу попадання випадкової величини, що розподілена за рівнимірним законом розв'язуйте за такою ж схемою. Вона проста і не вимагає складних обчислень.
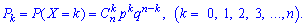
У табличній формі цей закон набирає такого вигляду:
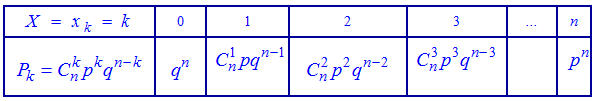
При перевірці виконання умови нормування використовується формула біному Ньютона, тому закон розподілу називають біноміальним
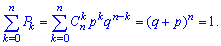 Побудуємо ймовірнісну твірну функцію для цього закону
Побудуємо ймовірнісну твірну функцію для цього закону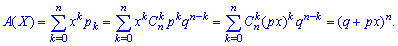 Отже, імовірнісна твірна функція для біноміального закону
Отже, імовірнісна твірна функція для біноміального закону Знайдемо основні числові характеристики для цього закону:
Знайдемо основні числові характеристики для цього закону:
1. Математичне сподівання випадкової величини через твірну функцію для біноміального розподілу матиме запис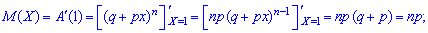
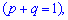
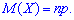
2. Друга похідна від твірної функції для біноміального розподілу в одиниці прийме значення

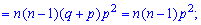
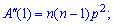
На основі знайденого значення можна обчислювати дисперсію за формулою
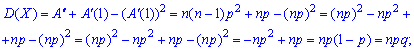
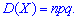 Маючи дисперсію не важко встановити середнє квадратичне відхилення
Маючи дисперсію не важко встановити середнє квадратичне відхилення
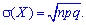
3. Коефіцієнт асиметрії А(Х) та ексцес Е(Х) для біноміального розподілу визначають за формулами
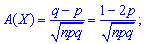
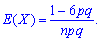
У випадку зростання кількості випробувань n асиметрія та ексцес прямують до нуля.
Розв'язи завдань на біноміальний розподіл
Задача 1. У партії однотипних деталей стандартні становлять 97%. Навмання з партії беруть 400 деталей. Визначити математичне сподівання, дисперсію та середнє квадратичне відхилення М(Х), D(X), S(Х) для дискретної випадкової величини Х — появи числа стандартних деталей серед 400 навмання взятих.
Розв'язання. Цілочислова випадкова величина Х має біноміальний закон розподілу ймовірностей, яка може набувати значення Х = k = 0, 1, 2, ..., 400. Імовірності можливих значень для даного завдання визначаються за формулою Бернуллі і становлять 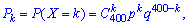 де р = 0,97 — імовірність появи стандартної деталі, q = 1 – p =1 – 0,97 = 0,03 — імовірність появи нестандартної деталі. Згідно з наведеними вище формулами визначаємо
де р = 0,97 — імовірність появи стандартної деталі, q = 1 – p =1 – 0,97 = 0,03 — імовірність появи нестандартної деталі. Згідно з наведеними вище формулами визначаємо
математичне подівання
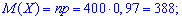
диперсію
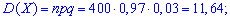
середнє квадратичне відхилення
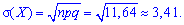
Розрахунки дя біноміального закону достатньо прості.
Задача 2. Два ювелірні заводи виробляють весільні кільця в об'ємі 3:7. Перший завод виготовляє 95% обручок без дефекту, другий – 90%. Молода пара перед весіллям купляє пару обручок. Побудувати закон розподілу, обчислити математичне сподівання та середнє квадратичне відхиленння.
Розв'язання. Імовірність події А – куплена обручка виявилася якісною визначимо за формулою повної імовірності
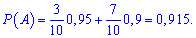
Випадкова величина Х – кількість кілець належної якості серед куплених має біноміальний закон розподілу з параметрами
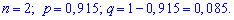
Знайдемо відповідні ймовірності
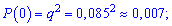
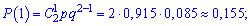
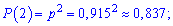
Та запишемо таблицю розподілу
 На основі табличних даних обчислюємо математичне сподівання
На основі табличних даних обчислюємо математичне сподівання

дисперсію
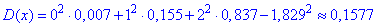
Середнє квадратичне відхилення через корінь з дисперсії прийме значення
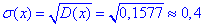
Як можна переконатися з прикладів, біноміальльний закон розподілу простий як для розуміння так ідля обчислень. Добре розберіться з прикладами та користуйтеся біноміальним розподілом там де це необхідно.
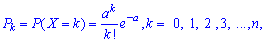 обчислюється за формулою Пуассона, де a=np<10. Як правило, Пуассонівський розподіл стосується ймовірності появи сприятливої події в великій кількості експериментів, якщо в одному – ймовірність успішного завершення прямує до нуля.
обчислюється за формулою Пуассона, де a=np<10. Як правило, Пуассонівський розподіл стосується ймовірності появи сприятливої події в великій кількості експериментів, якщо в одному – ймовірність успішного завершення прямує до нуля.У табличній формі цей закон розподілу має вигляд
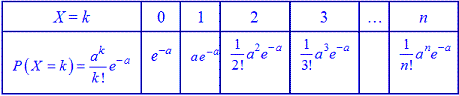 Умова нормування для пуасонівського закону розподілу запишеться наступним чином
Умова нормування для пуасонівського закону розподілу запишеться наступним чином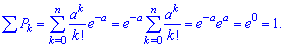 Побудуємо ймовірну твірну функцію для наведеного закону:
Побудуємо ймовірну твірну функцію для наведеного закону: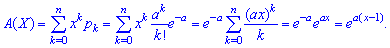 Вона приймає досить простий компактний вигляд
Вона приймає досить простий компактний вигляд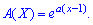 Скориставшись залежностями для визначення математичного сподівання М (Х) та дисперсії D (X) через похідні від твірної функції в одиниці, дістанемо їх прості залежності
Скориставшись залежностями для визначення математичного сподівання М (Х) та дисперсії D (X) через похідні від твірної функції в одиниці, дістанемо їх прості залежності
1. Математичне сподівання визначають за формулою
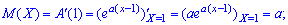
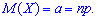
2. Маючи другу похідну від твірної функції в одиниці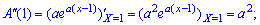 знаходять дисперсію
знаходять дисперсію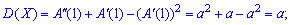
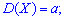 Середнє квадратичне відхилення встановлюємо через квадратний корінь з дисперсії
Середнє квадратичне відхилення встановлюємо через квадратний корінь з дисперсії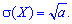 Отже, для пуассонівського закону розподілу ймовірностей математичне сподівання і дисперсія рівні добутку кількості дослідів на ймовірність сприятливої події
Отже, для пуассонівського закону розподілу ймовірностей математичне сподівання і дисперсія рівні добутку кількості дослідів на ймовірність сприятливої події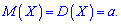 На практиці, якщо математичне сподівання і дисперсія близькі за значенням то приймають гіпотезу, що досліджувана величина має закон розподілу Пуассона.
На практиці, якщо математичне сподівання і дисперсія близькі за значенням то приймають гіпотезу, що досліджувана величина має закон розподілу Пуассона.
3. Асиметрія і ексцес для пуасонівського закону також рівні і обчислюються за формулами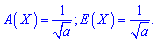
Задачі на Пуассонівський закон
Задача 1. Мікропроцесор має 10000 транзисторів, які працюють незалежно один від одного. Імовірність того, що транзистор вийде із ладу під час роботи приладу, є величиною малоймовірною і становить 0,0007. Визначити математичне сподівання М (Х) і середнє квадратичне відхилення S (Х) випадкової величини Х — числа транзисторів, що вийдуть із ладу під час роботи мікропроцесора.
Розв'язання. Задача задовільняє усім законам пуасонівського розподілу:
кількість випробувань n=10000 велика;
імовірність р=0,0007 близька до нуля;
їх добуток a=np=7<10.
На основі даних обчислюємо:
математичне сподівання M(X)
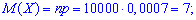
дисперсію
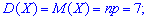
та середнє квадратичне відхилення
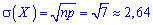
На контрольній чи тестах повтори обчислення не сладно, головне мати під рукою потрібні формули.
Задача 2. У рибальському містечку 99,99% чоловіків хоча б раз в житті були на рибалці. Проводять соціологічні дослідження серед 10000 навмання вибраних чоловіків. Визначити дисперсію D (X) і середнє квадратичне відхилення S (Х) випадкової величини Х — числа чоловіків, які жодного разу не були на рибалці.
Розв'язання. Легко переконатися, що величина Х має пуассонівський закон розподілу. Із умови задачі знаходимо
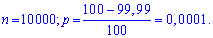
За формулами знаходимо дисперсію і середнє квадратичне відхилення
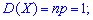
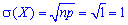
Можна знайти в гуглі ще багато подібних задач, всіх їх об'єднує зміна випадкової величини згідно закону Пуассона. Алгоритм знаходження числових характеристик наведений вище і є спільним для всіх задач, крім того формули для обчислень характеристик розподілу є достатньо простими навіть для школярів.
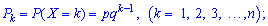
Тобто в усіх попередніх дослідах крім k-го експернимент дав поганий результат і лише в k-му був успішним. Дану формулу ймовірностей називають геометричним законом розподілу, оскільки права його частина співпадає з виразом загального елемента геометричної прогресію.
У табличній формі геометричний закон розподілу такий:
 При перевірці умови нормування використовується формула суми нескінченної геометричної прогресії
При перевірці умови нормування використовується формула суми нескінченної геометричної прогресії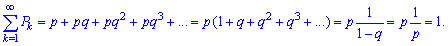 Ймовірнісну твірну функцію виражаємо за формулою
Ймовірнісну твірну функцію виражаємо за формулою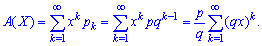 Оскільки
Оскільки 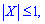 то твірну функцію можна просумувати
то твірну функцію можна просумувати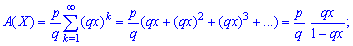
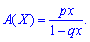
Числові характеристики для геометричного закону розподілу ймовірностей визначають за формулами:
1. Математичне сподівання обчислюємо за формулою
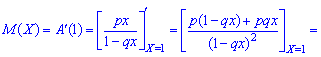
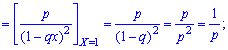
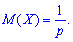
2. Дисперсію та середнє квадратичне відхилення з наступних заложнестей
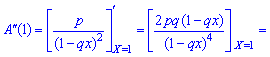
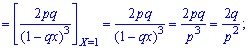
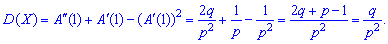
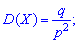
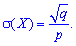
3. Коефіцієнт асиметрії та ексцес для геометричного розподілу визначають за формулою
![]()
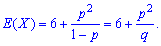
Серед дискретних випадкових величин лише геометричному закону притаманна властивість відсутності післядії. Це означає, що ймовірність появи випадкової події в k-му експерименті не залежить від того, скільки їх з'явилося до k-го, і завжди дорівнює p.
Приклад 1. Гральний кубик підкидається до першої появи цифри 1. Визначити усі числові характеристики М (Х), D (X), S (Х), A(X), E(X) для випадкової величини Х числа здійснюваних підкидань.
Розв'язання. За умовою задачі випадкова величина Х є цілочисловою з геометричним закон розподілу ймовірностей. Ймовірність успішного підкидання величина постійна і рівна одиниці розділеній на кількість граней кубика
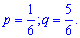
Маючи p,q необхідні числові характеристики Х знаходимо за наведеними вище формулами
математичне сподівання
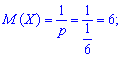
дисперсію
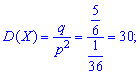
середнє квадратичне відхилення
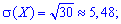
асиметрію
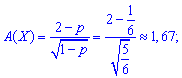
та ексцес
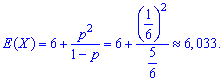
Якби всі формули ймовірності були б на стільки легкі, то можна було б її повністю перенести в шкільну програму. Однак поки що це нереально реалізвати.
Приклад 2. Мисливець-любитель стріляє з рушниці по нерухомій мішені. Імовірність влучити в мішень при одному пострілі є величиною сталою і дорівнює 0,65. Стрільба по мішені ведеться до першого влучення.
Визначити числові характеристики М (Х), D (X), S (Х), A(X), E(X) випадкової величини Х — числа витрачених мисливцем набоїв.
Розв'язання. Випадкова величина Х підпорядковується геометричниму закону розподілу тому ймовірність влучання в кожній спробі є сталою і становить p=0,65;q=1-p=0,35.
За формулами ймовірності обчислюємо математичне сподівання
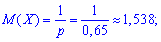
дисперсію
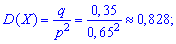
середнє квадратичне відхилення
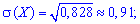
асиметрію
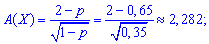
ексцес
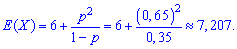
Обчислення числових характеристик для геометричного закону розподілу під силу кожному, тому користуйтеся наведеними формулами в подібних задачах і отримуйте лише правильні результати.
Для дослідження законів розподілу цілочислових випадкових величин використовують імовірнісну твірну функцію. Імовірнісною твірною функцією називають наступний збіжний степеневий ряд:
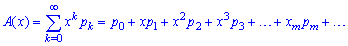
Тут pk=P(X=k) – ймовірність того, що випадкова величина Х набуде цілих значень k=0, 1, 2, 3, … .
Саме тому розділ починається з твірних функцій. Дочитавши всі статті розділу до кінця Вам стане зрозуміло, чому в усіх законах розподілу присутня імовірнісна твірна функція.
ВЛАСТИВОСТІ ІМОВІРНІСНОЇ ТВІРНОЇ ФУНКЦІЇ
1. Твірна функція А(Х) визначена в кожній точці інтервалу [–1; 1].
2. При Х=1 виконується справедливість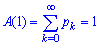 Співвідношення є умовою нормування для дискретної випадкової величини.
Співвідношення є умовою нормування для дискретної випадкової величини.
3. Із залежності для твірної функції А(Х) визначають ймовірність P(k)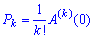 де
де 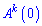 — k-та похідна від твірної фнкції А(х) при Х = 0.
— k-та похідна від твірної фнкції А(х) при Х = 0.
Отже, знаючи аналітичний вираз для А(х), завжди можна визначити ймовірність будь-якого можливого значення Х=k.
4. Похідна від твірної функції визначається співвідношенням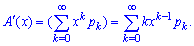 При х = 1 похідна рівна математичному сподіванню
При х = 1 похідна рівна математичному сподіванню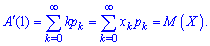 Звідси отримаємо
Звідси отримаємо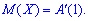 5. Визначимо другу похідну твірної функції
5. Визначимо другу похідну твірної функції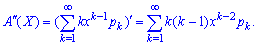 При х = 1 друга похідна приймає значення
При х = 1 друга похідна приймає значення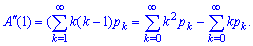 Отриманий вираз можна переписати в зручній формі:
Отриманий вираз можна переписати в зручній формі: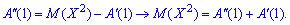 На основі цього, дисперсію через похідні першого та другого порядків твірної функції
На основі цього, дисперсію через похідні першого та другого порядків твірної функції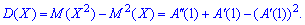 можна переписати в спрощеній формі
можна переписати в спрощеній формі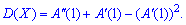 ЇЇ часто використовують на практиці, при обчисленні дисперсії коли задана імовірнісна твірна функція або можна її визначити. Розглянемо варіант, коли маємо безліч несумісних подій, які виконуються при незалежних випробуваннях з ймовірністю p1,p2,...,pn. Тоді твірна функція визначається із співвідношення
ЇЇ часто використовують на практиці, при обчисленні дисперсії коли задана імовірнісна твірна функція або можна її визначити. Розглянемо варіант, коли маємо безліч несумісних подій, які виконуються при незалежних випробуваннях з ймовірністю p1,p2,...,pn. Тоді твірна функція визначається із співвідношення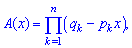 де
де 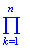 – знак добутку, qk – ймовірність несприятливої події, яка визначається за правилом
– знак добутку, qk – ймовірність несприятливої події, яка визначається за правилом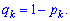 Розглянемо приклади застосування твірної функції.
Розглянемо приклади застосування твірної функції.
Приклад 1. Чотири лісовози незалежно один перевозять ліс до лісопилки. Ймовірність поламки в дорозі кожної з машин становить 0,9 для першої; для другої – 0,85; для третьої – 0,8 і 0,75 для останньої. Яка ймовірність того, що без поломок доїде три лісовози з чотирьох? Яка ймовірність, що не більше двох лісовозів доїдуть справними до лісопилки?
Розв'язання. Імовірності кожної з подій різні та утворюють незалежні випробування. Для відшукання відповіді на обидва запитання побудуємо твірну функцію.
Для неї вхідні дані приймуть заначення
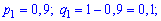
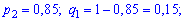
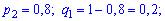
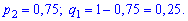
Підставимо знайдені величини в твірну функцію
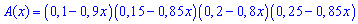
та розкладемо в ряд за степенями змінної. В результаті отримаємо поліном
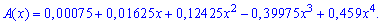
За властивостями твірної функції коефіцієнти при степенях аргументів є ймовірностями виконання події (довезення лісу без поломки) рівно стільки раз – який степінь аргумента.
На основі цього, ймовірність події Р(А), що доїде три лісовози без поломки входить в твірну функцію при x3 і становить
Р(А)=0,39975.
Ймовірність події Р(B) можна росписати як суму ймовірностей, що доїде один лісовоз + доїде два лісовози+не доїде жодного.
Відповіді названим доданкам ймовірності шукаємо при відповідних їм степенях твірної функції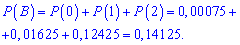
Як бачите обчислення не складні, головне зрозуміти суть завдання. Також можете переконатися, що виконується умова нормування
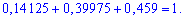
Якщо трапиться, що при обчисленнях у Вас не виконується умова нормування, тоді потрібно шукати помилку при розкладі твірної функції в ряд за степенями х і виправити її.
Нехай задано деяку множину однотипних елементів, число яких дорівнює N; з них K елементів мають, наприклад, ознаку А (колір, стандартність, наповнення), а решта N-K елементів — ознаку В. З цієї множини навмання беруть n елементів. Випадкова величина X – число елементів з ознакою А, що трапляється серед n навмання взятих елементів. Тоді X набуває значень k=0,1,2,...,min(n,K) , а ймовірність їх появи визначається за гіпергеометричним законом
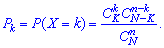
У табличній формі запису цей закон розподілу має вигляд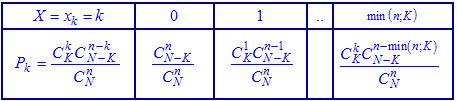 Нагадаємо, що сполучення знаходять за формулою
Нагадаємо, що сполучення знаходять за формулою![]() а факторіал функцію за правилом–
а факторіал функцію за правилом– 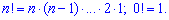
При n=k і k=0 сполучення рівне одиниці.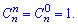 Умова нормування для гіпергеометричного розподілу має вигляд
Умова нормування для гіпергеометричного розподілу має вигляд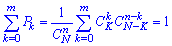 Залежно від умови задачі найменше значення може становити m = 0, 1, 2, 3, ..., m.
Залежно від умови задачі найменше значення може становити m = 0, 1, 2, 3, ..., m.
Числові характеристики цього закону обчислюються за наведеними нижче формулами:
1. Математичне сподівання
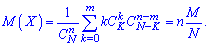
2. Дисперсія і середнє квадратичне відхилення
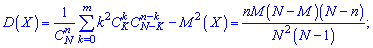
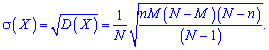
3. Формула для асиметрії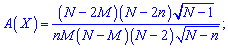 та ексцесу
та ексцесу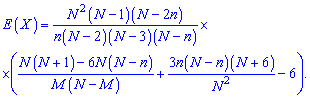 формули мають досить громіздкий вигляд, тому їх, як правило, обчислюють в екселі, чи математичних програмах (Maple, MathCad, Mathematica).
формули мають досить громіздкий вигляд, тому їх, як правило, обчислюють в екселі, чи математичних програмах (Maple, MathCad, Mathematica).
Розглянемо декілька прикладів на застосування наведених вище формул.
Приклад 1. В ящику міститься 10 однотипних деталей, із них 7 стандартних, а решта є бракованими. Навмання із ящика беруть m деталей. Побудувати закони розподілу цілочислової випадкової величини Х — появу числа стандартних деталей серед m навмання взятих і обчислити математичне сподівання М(Х), дисперсію D (X), та середнє математичне відхилення S(Х), якщо:
I. m = 3;
II) m = 4;
III) m = 5;
IV) m = 7.
Розв'язання. Використовуючи наведені вгорі формули побудуємо гіпергеометричні закони розподілу:
I. Маємо наступні початкові умови для випадку вибору трьох деталей
n = 3; N=10; K= 7; N-K= 3; k = 0, 1, 2, 3.
У табличній формі гіпергеометричний закон для цих даних має вигляд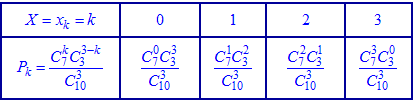 або після обчислення сполучень
або після обчислення сполучень
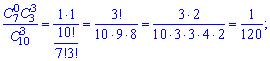
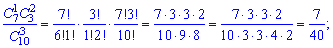
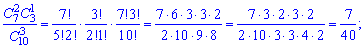
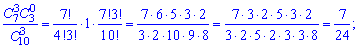
у вигляді таблиці ймовірностей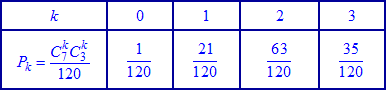 Умова нормування
Умова нормування
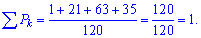
виконується, отже все вірно пораховано. Не лінуйтеся первіряти її, вона саме швидше вкаже Вам на присутність помилки при неправильній правій частині. Обчислюємо числові характеристики:
математичне сподівання
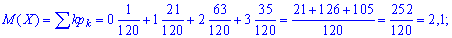
Дисперсію
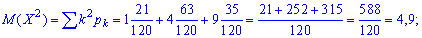
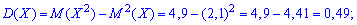
Середнє квадратичне відхилення
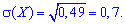
ІІ. Вибирають чотири деталі
n=4; K=7; N-K=3; k=1, 2, 3, 4.
У табличній формі закон розподілу запишеться формулами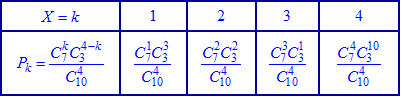 або після обчислень у вигляді таблиці
або після обчислень у вигляді таблиці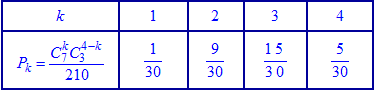 Перевіряємо умову нормування для знайдених значень.
Перевіряємо умову нормування для знайдених значень.
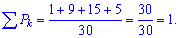
Вона виконується, отже можемо обчислювати числові характеристики за наведеними вище формулами:
математичне сподівання прийме значення
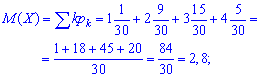
дисперсію і середнє квадратичне відхилення визначаємо за схемою попередньої задачі
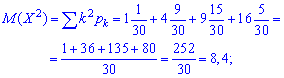
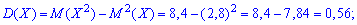
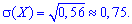
ІІІ. Вибирають п'ять деталей
т=5; K=7; N-K=3; k=2, 3, 4, 5.
У табличній формі закон подається так:
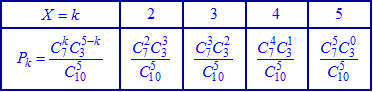 або після обчислень у вигляді таблиці значень
або після обчислень у вигляді таблиці значень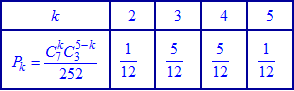 Умова нормування
Умова нормування
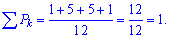
виконується. Обчислюємо математичне сподівання
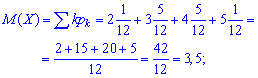
Складову дисперсії
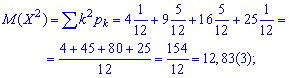
та саму дисперсію
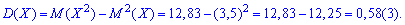 .
.
середнє квадратичне відхилення за відомою дисперсією
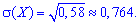
IV.) Вибирають сім деталей
т=7; K=7; N-K=3; k=4, 5, 6, 7.
У табличній формі даний розподіл приймає значення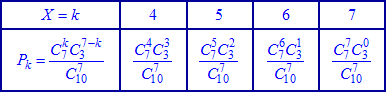 або після обчислень
або після обчислень
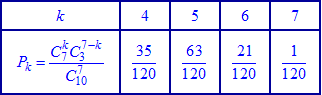
Умова нормування
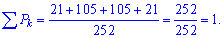
виконується.
Числові характеристики визначаємо на основі формул:
математичне сподівання
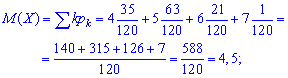
математичне сподівання квадрату величини
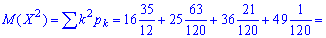
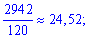
дисперсію
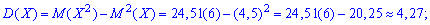
середнє квадратичне відхилення
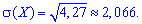
На цьому розв'язування задачі завершено. Будьте уважними при розв'язуванні прикладів на гіпергеометричний розподіл, оскільки досить часто потрібно знаходити сполучення 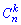 і при спрощенні факторіалів можна допустити помилку.
і при спрощенні факторіалів можна допустити помилку.