Для опису рівня залежності між випадковими величинами X і Y в основному використовують дві числові характеристики: коваріація та коефіцієнт кореляції.
Коваріацією або кореляційним моментом системи випадкових величин X і Y називають число, розраховане за формулою
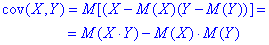
Математичні сподівання кожної з випадкових величин можна обчислити попередньо.
Тоді формула кореляційного моменту для дискретних значень прийме вигляд
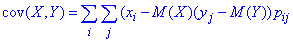
Коефіцієнтом кореляції для системи двох випадкових величин називають число, яке знаходять за формулою
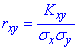
Наступні твердження слід запам'ятати, оскільки їх часто запитують при тестуванні з ймовірності та на контрольних.
Якщо випадкові величини X і Y незалежні, то коваріація та коефіцієнт кореляції рівні нулю
cov (X, Y)=r (X, Y)=0.
Обернене твердження невірне.
Тому, що можна навести приклади залежних випадкових величини, для яких коваріація та коефіцієнт кореляції дорівнюють нулю.
Для довільних випадкових величин коефіцієнт кореляції обмежений за модулем одиницею
–1≤r (X, Y)≤1.
Чим коеф. кореляції |r(X, Y)| ближчий до одиниці, тим сильнішим вважають рівень залежності між X і Y.
Якщо r(X, Y)=0, то випадкові величини називаються некорельованими.
Приклад 1 Дано закон розподілу дискретної двовимірної випадкової величини (X, Y).
Знайти коефіцієнт кореляції між X і Y.

Обчислення: Перепишемо таблицю в наступному вигляді та знайдемо середні ймовірності
X\Y | -1 | 0 | 1 | P[xi] |
1 | 0.15 | 0.15 | 0.25 | 0.55 |
2 | 0.1 | 0.15 | 0.2 | 0.45 |
P[yi] | 0.25 | 0.3 | 0.45 | 1 |
Коефіцієнт кореляції обчислюємо за формулою
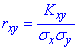
тут кореляційний момент рівний
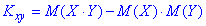
Знайдемо складові.
Математичне сподівання знайдемо за формулою
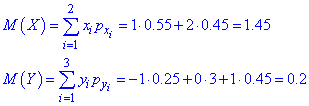
Математичне сподівання від добутку випадкових величин рівне
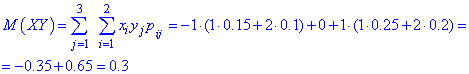
Знайдемо дисперсію D(X), D(Y)

та середнє квадратичне відхилення 
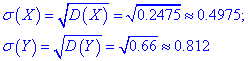
Обчислюємо коваріаційний момент
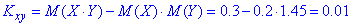
та підставляємо в формулу коефіцієнта кореляції
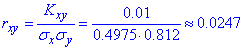
Випадкові величини близькі до некорельованих, оскільки значення близьке до нуля.
Приклад 2 Одержано n=100 значень пари випадкових величин (X, Y) записаних в кореляційній таблиці.
Знайти коефіцієнт кореляції між X і Y.

Обчислення: Перетворимо таблицю до ймовірнісних значень
X \Y | -1 | 0 | 1 | 2 | P(xi) |
1 | 0,25 | 0,05 | 0 | 0 | 0.3 |
2 | 0 | 0,2 | 0,1 | 0,1 | 0.4 |
3 | 0 | 0,15 | 0,15 | 0 | 0.3 |
P(yi) | 0.25 | 0.4 | 0.25 | 0.1 | 1 |
Коефіцієнт кореляції знайдемо за формулою
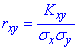 (1)
(1)
де кореляційний момент знайдемо із залежності
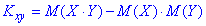
Формули математичного сподівання кожної з випадкових величин та їх добутку приймуть значення
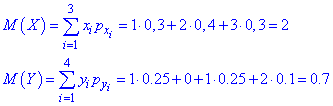
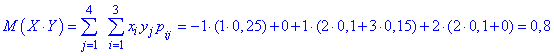
Знайдемо дисперсію D(X), D(Y)
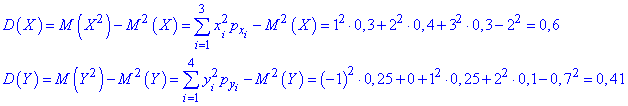
та середнє квадратичне відхилення 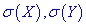
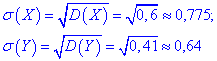
Обчислюємо кореляційний момент
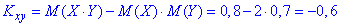
Далі знаходимо коефіцієнт кореляції
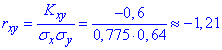
Розв'яжемо ще один приклад, щоб закріпити матеріал.
Приклад 3 Одержані n=100 значень пари випадкових величин (X, Y) записаних в кореляційній таблиці.
Знайти коефіцієнт кореляції між X і Y.

Обчислення: Перепишемо таблицю до ймовірнісних значень, попередньо пронормувавши, щоб сума всіх елементів стала рівною одиниці
X \Y | 0 | 1 | 2 | 3 | P(xi) |
1 | 0,05 | 0,14 | 0,11 | 0 | 0.3 |
2 | 0 | 0,06 | 0,14 | 0,2 | 0.4 |
3 | 0 | 0,15 | 0,1 | 0,05 | 0.3 |
P(yi) | 0.05 | 0.35 | 0.35 | 0.25 | 1 |
Обчислення: Для підрахунку коефіцієнта кореляції (1) необхідно знати математичні сподіванні та середні квадратичні відхилення, тому почергово їх обчислюємо.
Знайдемо математичні сподівання
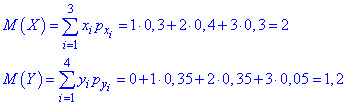
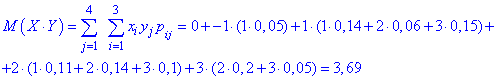
Обчислимо дисперсії обох величин D(X), D(Y)
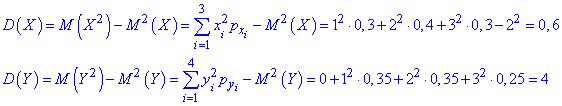
та середні квадратичні відхилення  через корінь з дисперсії
через корінь з дисперсії
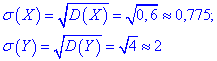
Обчислюємо коваріацію
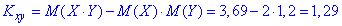
Далі знаходимо коефіцієнт кореляції
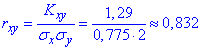
Розрахунки не важкі, якщо мати наведений алгоритм знаходження коефіцієнту кореляції то все решта залежить від Вашого бажання обчислювати.
- Вас може зацікавити:
- Знайти моду, медіану, дисперсію може кожен!
- Дисперсія та середнє квадратичне відхилення
- Система двох дискретних випадкових величин (X, Y). Обчислення числових характеристик
- Як перевірити гіпотезу про нормальний розподіл генеральної сукупності ?
- Функція розподілу ймовірностей дискретної величини


