Область, на яку поширюється геометричне означення ймовірності, може бути одновимірною (пряма, відрізок), двовимірною (плоска фігура) і тривимірною (деяке тіло у просторі).
Якщо позначити міру (довжину, площу, об'єм) області через size, то прийдемо до такого геометричного означення ймовірності:
геометричною імовірністю події A називається відношення міри області, яка сприяє події A, до міри всієї області
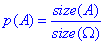
- Самі ж задачі на геометричну ймовірність мають наступні формулювання:
- знайти ймовірність попадання точки в інтервал,
- знайти ймовірність попадання точки в площу,
- знайти ймовірність попадання точки в об'єм.
Найпростіші задачі на геометричну ймовірність розв'язують за допомогою відомих формул для площ та об'ємів.
Більш складні завдання вимагають знаходження площі та об'єму через інтегрування, що в свою чергу вимагає правильного визначення меж інтегралів.
Готові відповіді до прикладів на знаходження геометричної ймовірності із застосуванням інтегрування та без нього будуть роглянуті після опису класифікації задач та властивостей геометричної ймовірності.
Основні схеми знаходження геометричної ймовіврності
Геометрична ймовірність зберігає всі ознаки та властивості класичної ймовірності
Задачі на геометричну ймовірність з відповідями
Задача 1 В круг вписано квадрат. У круг навмання кидають точку.
Знайти ймовірність того, що вона виявиться всередині квадрата.
Обчислення: Для кращого уявлення виконаємо графічний малюнок до задачі
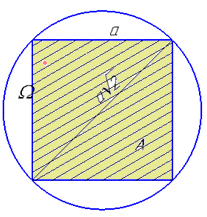
Нехай сторона квадрата A дорівнює a, тоді його площа –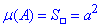 
.
Діаметр круга 
, що описаний навколо квадрата дорівнює діагоналі квадрата рівний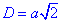 
, тоді площа цього круга:
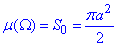
Оскільки квадрат знаходиться всередины круга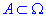 
, то ймовірність того, що навмання кинута точка в круг виявиться всередині квадрата обчислюється за формулою:
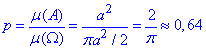
Відповідь: p=0,64
Задача 2 Два судна повинні підійти до одного причалу. Поява суден – незалежні події, рівноможливі протягом доби.
Знайти ймовірність того, що одному з суден доведеться чекати звільнення причалу, якщо час стоянки першого судна – 1 год, а другого – 2 год.
Обчислення: Нехай перше судно прийшло до причалу в u год і стоїть 1 годину, а друге судно прийшло до того ж причалу в v год і стоїть 2 години.
За простір елементарних подій виберемо
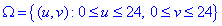
звідси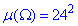 
(площа).
Тоді подія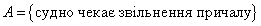 
відповідає множині (заштрихована фігура на рис. далі)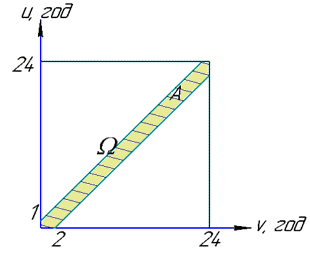 
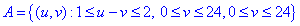
звідси її площа:
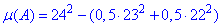
Оскільки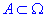 
, то ймовірність того, що одному з суден доведеться чекати звільнення причалу знайдемо за формулою:
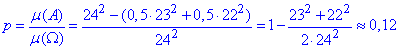
Відповідь: p=0,12.
Задача 3 На площину, на якій зображені паралельні прямі, що розташовані одна від одної на відстані 6 см, навмання кинули круг радіусом 1 см.
Знайти ймовірність того, що круг не перетне жодної прямої. По замовчуванню розуміється, що ймовірність попадання точки на відрізок пропорційна довжині відрізку і не залежить від його розташування.
Обчислення: Нехай D=6 см – відстань між паралельними прямими;
d=2r=2 см – діаметр круга, який кинули на площину.
Схематично це можна візуалізувати наступним чином: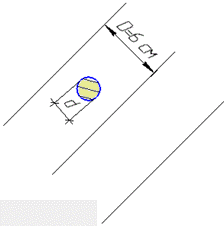 
Ймовірність того, що круг не перетне жодної прямої знаходимо наступним чином:
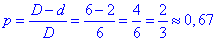
де D-d=4 см – найкоротша відстань від кола (яким обмежений круг) до паралельних прямих.
Як бачимо така ймовірність є протилежною до того, що навмання кинутий круг перетне хоча б одну пряму:
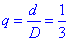
Відповідь: p=0,66(6).
Задача 4 Навмання взято два додатних числа x і y, кожне з яких не перевищує одиниці.
Знайти ймовірність того, що сума x+y не перевищує одиниці, а добуток x•y не менше 0,09.
Обчислення: За умовою задачі маємо
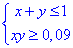
а також обмеження на змінні
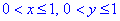
Розв'язавши систему нерівностей отримаємо:
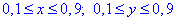
За простір елементарних подій виберемо
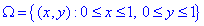
звідси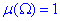 
(площа).
Тоді подія
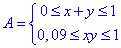
відповідає множині (заштрихована фігура на рис. далі)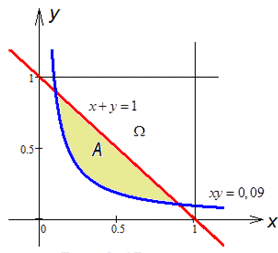 
Побудова рисунків до задач на геометричну ймовірність дає повніше розуміння, що потрібно знайти.
Якість малюнку ролі не грає, головне зміст, тому всюди де потрібно будуйте графічні схемки до умов задач.
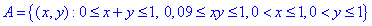з відповідними межами області A:
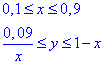
На основі меж змінних можемо знайти площу між кривими через визначений інтеграл:
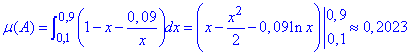
Оскільки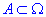 
, то ймовірність шуканої події знайдемо за формулою частки:
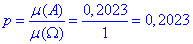
Відповідь: p=0,2023.
Подібних задач в інтернеті чимало, час від часу cтудентам задають складніші, їх ми розв'язуємо на замовлення.
Наведених прикладів Вам достатньо, щоб почати розв'язувати приклади на геометричну ймовірність самостійно.
Використана література:
1) Бордуляк М. Т. Теореми і задачі теорії ймовірності: навч. посібн. / М. Т. Бордуляк, О. Б. Скасків, О. М. Сумик, І. Е. Чижиков – Львів: Видавець І. Е. Чижиков, 2013. – 175 с. – (Серія «Математичний практикум»).
2) Сеньо П. С. Теорія ймовірностей та математична статистика: Підручник. – 2-ге вид., перероб. і доп. – К.: Знання, 2007. – 556 с.
3) Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. Учеб. пособие для втузов – Изд. 2-е, стер. – М.: «Высшая школа». – 1975. – 333 стр. с илл.
