В попередній статті детально розібрано кілька задач на повну ймовірність, показано як позначати гіпотези та знаходити їх ймовірність.
Сьогодні завдання – навчитися застосовувати теорему Байєса.
Формула Байєса містить повну ймовірність в знаменнику дробу, а в чисельнику умовну ймовірність.
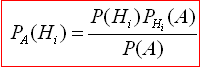
Щоб детально розібратися що за що відповідає уважно перегляньте наступні готові відповіді до прикладів.
Приклад 1 В першій урні 5 білих і 3 чорних кульки, в другій урні 6 білих і 4 чорних кульки.
З навмання вибраної урни взяли кульку, яка виявилась білою.
Яка ймовірність, що вона взята з другої урни?
Обчислення: Позначимо через А подію, що вийнята кулька біла.
В першій урні маємо 5+3=8 кульок, в другій 6+4=10. Сумарно маємо 10+8=18 кульок.
Нехай B, C – гіпотези, що кулька вийнята з першої та другої урни відповідно.
Взагалі кажучи гіпотези можна позначати будь-якою великою літерою латинського алфавіту.
Але це доцільно робити коли їх не більше 3.
Коли 3 і більше то доречно використовувати одну велику літеру і номер гіпотези, наприклад H1,H2,H3,H4
(H від слова hypothesis – гіпотеза, припущення).
Таким чином легше виписувати ймовірності та контролювати, що й до чого належить.
Позначимо через P(B), P(C) – ймовірності вийняти кульки з першої та другої урни.
Вони рівні частці кульок в загальній сукупності, тобто
P(B)=8/18=8/18;
P(C)=10/18.
Ймовірність вийняти білу кульку з першої урни рівна частці білих кульок в ній
P(A/B)=5/8.
Це умовна ймовірність і тлумачити її можна так:
якщо вибрана перша урна (B), то ймовірність вийняти білу кульку (ймовірність події А) рівна P(A/B).
Умовну ймовірність ще позначають P(A|B), PB(A), то ж не дивуйтеся якщо викладач саме в таких позначеннях буде пояснювати ймовірнісні задачі.
Відповідне значення ймовірності вийняти білу кульку з другої урни рівне
P(A/C)=6/10.
Ймовірність вийняти білу кульку рівна повній ймовірності, яка в свою чергу рівна сумі попарних добутків ймовірності гіпотез на умовні ймовірності події А при підтвердженні гіпотез:
P(A)=P(B)·P(A/B)+P(C)·P(A/C)=8/18·5/8+10/18·6/10=11/18=0.6(1)
Ймовірність вийняти білу кульку з другої урни рівна вкладу 2 доданку в попередній ймовірності
P(C/A)=P(C)·P(A/C)/P(A)=6/18/(11/18)=6/11=0,54(54)
Попередній запис і є відомою формулою Байєса, а ймовірність рівна
P(C/A)=0,54(54)
Відповідь: 0,54(54).
Далі пояснення будуть менш деталізовані, але головна суть методу Байєса Вам повинна бути зрозуміла.
Приклад 2 Дві секретарки заповнюють документи, які складають у спільну папку.
Ймовірність того, що помилки в документі зробить перша секретарка, становить 0,04, а друга-0,2.
Перша секретарка заповнила 40 документів, друга-30.
Навмання взятий документ із папки виявився з помилками.
Визначити ймовірність того, що його заповнювала друга секретарка.
Обчислення: Позначимо через H1,H2 гіпотези, що документи заповняли перша та друга секретарки відповідно.
Подія А відповідає тому, що навмання взятий документ виявився з помилками.
Ймовірність взяти документ першої та другої секретарки рівні
P(H1)=30/(30+40)=3/7;
P(H2)=40/70=4/7.
Ймовірність, що помилки зробили секретарки рівні
P(A/H1)=0,04;
P(A/H2)=0,2.
Тоді ймовірність події А знаходимо за формулою повної ймовірності
P(A)= P(H1)• P(A/H1)+ P(H2)• P(A/H2)= 3/7•0,04+4/7•0,2=0,131
Ймовірність того, що документ з помилкою заповнювала друга секретарка знайдемо за формулою Байєса
P(A/H2)= P(H2)•P(A/H2)/ P(A)= 4/7•0,2/0,131=0,87
Відповідь: 0,87.
Приклад 3 У змаганнях з шахів беруть участь 5 студентів економічного, 3 – біологічного, 4 – географічного та 4 - математичного факультетів.
Серед учасників є троє дівчат з економічного, одна з біологічного та по дві з географічного та математичного факультетів.
Навмання вибраний учасник виявився дівчиною.
Яка ймовірність, що він навчається на економічному факультеті?
Обчислення: Завдання на знання формул повної ймовірності та Байєса. Подія А – навмання вибраний студент є дівчиною.
Позначимо через Н1, Н2, Н3, Н4 гіпотези, що обраний студент навчається на економічному, біологічному, географічному та математичному факультеті.
Тоді ймовірності зроблених гіпотез рівні долі студентів кожного з факультетів у загальній їх кількості:
p(H1)=5/(5+3+4+4)=5/16;
p(H2)=3/16;
p(H3)=4/16=1/4;
p(H4)=4/16=1/4.
Умовні ймовірності події А за умови, що вибраний певний факультет рівні частці кількості дівчат на кожному факультеті до загальної кількості студентів, тобто
p(A/H1)=3/5;
p(A/H2)=1/3;
p(A/H3)=2/4=1/2;
p(A/H4)=1/2.
Ймовірність, що навмання обраний студент – дівчина, обчислимо за формулою повної ймовірності
P(A)= P(H1)•P(A/H1)+P(H2)•P(A/H2)+P(H3)•P(A/H3)+P(H4)•P(A/H4)=
= 5/16•3/5+3/16•1/3+1/4•1/2+1/4•1/2=0,5.
Ймовірність, що дівчина навчається на економічному факультеті знаходимо за формулою Байєса
P(H1/A)= P(H1)•P(A/H1)/P(A)=0,1875/0,5=0,375.
Це також умовна ймовірність.
Відповідь: 0,375.
Приклад 4 Василь, Тарас і Андрій працюють у банку. За день Василь обслуговує 12 клієнтів, Тарас – 25, Андрій – 10.
Ймовірність того, що при розмові з Василем клієнт захоче користуватися послугами банку становить 0,7, з Тарасом – 0,6 і з Андрієм – 0,8.
Навмання вибраний клієнт користувався послугами банку.
Визначити ймовірність того, що цю послугу оформив Василь.
Обчислення: Приймемо через H1,H2,H3 гіпотези, що послугу оформляли Василь, Тарас та Андрій відповідно.
Ймовірності гіпотез пропорційні кількості клієнтів, обслужених кожним з працівників
P(H1)=12/(12+25+10)=12/47;
P(H2)=25/47;
P(H3)=10/47.
Подія А полягає в тому, що вибраний клієнт користувався послугами банку.
Якщо клієнт розмовляв з Василем, то ймовірність скористатися послугами банку рівна 0,7.
Тобто маємо умовну ймовірність події А.
Для Василя та 2 інших працівників відповідні ймовірності рівні
P(A/H1)=0,7;
P(A/H2)=0,6;
P(A/H3)= 0,8.
Через формулу повної ймовірності оцінимо чи навмання вибраний клієнт користувався послугами банку
P(A)= P(H1)•P(A/H1)+P(H2)•P(A/H2)+P(H3)•P(A/H3)=
=12/47•0,7+25/47•0,6+10/47•0,8=0,668.
Ймовірність, що послугу оформляв Василь знайдемо за формулою Байєса
P(A/H1)= P(H1)•P(A/H1)/ P(A)= 12/47•0,7/0,668=0,26755.
Відповідь: 0,26755.
Приклад 5. У першій урні 2 білих та 6 чорних куль, у другій – 4 білих та 2 чорних. З першої урни навмання переклали 2 кулі в другу, після чого з другої урни навмання дістали одну кулю.
а) Яка ймовірність того, що ця куля біла?
б) Ймовірність що переклали дві чорі кулі, якщо взята з другої урни, виявилася білою.
Яка ймовірність того, що з першої урни в другу були перекладені 2 білі кулі?
Розв'язування: Результат вибору кульки залежить від того, які кулі переклали.
1) переклали два білі ⇒ у другому кошику стало 6 білих та 2 чорних.
p=6/8 – ймовірність вийняти білу кулю
2) переклали два чорні ⇒ у другому кошику стало 4 білих та 4 чорних.
p=4/8 – ймовірність вийняти білу кулю
3) переклали один білий та один чорний ⇒ у другому кошику стало 5 білих та 3 чорних.
p=5/8 – ймовірність вийняти білу кулю.
Це напряму випливає з того, які набори кульок отримали в другій урні.
Записуємо події - гіпотези:
H1–"переклали дві білих"
H2–"переклали дві чорні"
H3–"переклали чорну, білу"
H4-"переклали білу, чорну".
Ймовірність гіпотез залежить від кількості мячів того чи іншого кольору, тому
p(H1)=2/8*1/7=2/56;
p(H2)=6/8*5/7=30/56;
p(H3)=p(H4)=6/8*2/7=12/56.
Гіпотези утворюють повну групу подій
p(H1)+p(H2)+p(H3)+p(H4)=1.
а) Подія A-"з другого кошика витягнуто білу кулю":
Випишемо скільки яких куль стало в другій урні та ймовірності події
6 б і 2 ч p(A/H1)=6/8;
4 б і 4 ч p(A/H2)=4/8;
5 б і 3 ч. p(A/H3)=5/8;
5 б і 3 ч p(A/H4)=5/8.
Тоді за формулою повної ймовірності маємо:
p(A)=2/56·6/8+30/56·4/8+12/56·5/8+12/56·5/8=9/16
б) за формулою Байєса знаходимо ймовірність, що переклали дві чорні,якщо вийняли білу кулю:
p(H2/A)=p(A/H2)*p(H2)/p(A)=30/56·4/8:(9/16)=10/21.
Відповідь: 9/16, 10/21.
Приклад 6. Правління підприємства складається з 9 осіб. Скількома способами можна з цих людей обрати трьох керівників - президента, директора та комерційного директора?
Розв'язування: На роль директора можна обрати 1 з 9 осіб, тоді залишиться 8, тому на роль президента 1 з 8, після чого залишиться 7 кандидатів на роль комерційного директора.
Тому кількість всіх способів обрати трьох керівників рівна:
N=9*8*7=504
Відповідь: 504.
На цьому поки що розгляд формули Байєса завершено.
При виконанні замовлень з ймовірності задачі на повну ймовірність та формулу Байєса зустрічаються в широкої аудиторії студентів, тож добре розберіть для себе алгоритм обчислень та наведену структуру пояснень до задач.


