Тригонометричні нерівності зі складним аргументом за методом розв'язування не надто відрізняються від простих тригонометричних нерівностей, на початку виконуємо заміну змінних, далі розв'язуємо нерівність. Далі повертаємося до заміни змінних, щоб врахувати складний аргумент. Далі будуть наведені готові відповіді до тригонометричних нерівностей, які потрібно вміти розв'язувати при проходженні зовнішнього незалежного оцінювання та вступі у ВУЗи на факультети з математичними дисциплінами.
Завдання 19.9 Розв'язати нерівність cos(2x)≥-√2/2.
Розв'язання: Спершу виконуємо перевірку чи права частина нерівності відповідає області допустимих значень косинуса.
Оскільки умова |-√2/2|≤1 виконується, то розв'язок нерівності існує.
Зробимо заміну змінних: t=2x та перейдемо до обчислень простішої нерівності
cos(t)≥-√2/2.
Графічний метод, що ілюстрували для найпростіших тригонометричних нерівностей тут наводити не будемо.
Всі хто зацікавлені можуть переглянути попередню статтю.
Далі у всіх прикладах обчислення проміжків виконання нерівності будемо виконувати на одиничному колі.
Для цього в декартовій системі координат будуємо одиничне коло та пряму y=-√2/2, що є константою в правій частині за знаком нерівності.
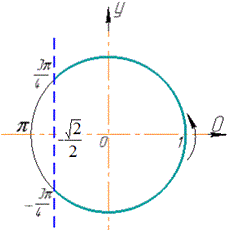
Далі позначаємо точки Pt1 і Pt2 перетину одиничного кола й зазначеної прямої та виділимо множину точок (виділено синім на графіку), ординати яких не менші -√2/2.
Не менші, тому що нерівність нестрога і всі значення косинуса мають бути більші або рівні -√2/2.
Знайдемо значення t1 і t2, здійснюючи обхід дуги кола проти годинникової стрілки:
t1<t2,
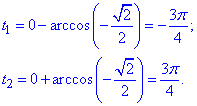
Далі врахуємо, що період косинуса рівний 2Пі та записуємо розв'язок нерівності у вигляді проміжків
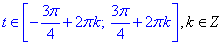
або двосторонньої нерівності
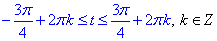
Повернемося до заміни t=2x, щоб перерахувати кути
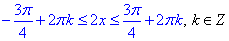
Остаточно, отримаємо
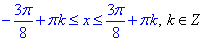
(поділили кожну частину нерівності на 2).
Множиною розв'язків нерівності є точки
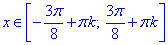
Завдання 19.10 Розв'язати нерівність sin(3x)≥√2/2.
Розв'язання: Перевіряємо ОДЗ синуса: |√2/2|≤1, отже нерівність має розв'язок.
Робимо заміну змінних: t=3x.
Після заміни нерівність спроститься до наступної:
sin(t)≥√2/2.
Будуємо одиничне коло, пряму y=√2/2.
Позначаємо точки перетину одиничного кола й зазначеної прямої та виділяємо множину точок, ординати яких не менші √2/2.
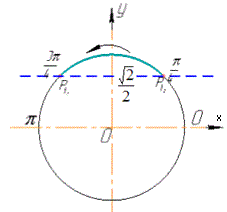
Знайдемо значення t1 і t2, виконуючи обхід дуги проти годинникової стрілки: t1<t2,
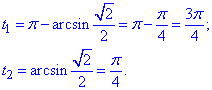
Обхід слід виконувати проти годинникової стрілки, тому що в цьому напрямку зростає градусна міра кута від 0 до 2Пі.
Якщо цього не робити, то у Вас вийде, що початковий кут є більшим за кінцевий, що неможливо.
Додаємо період синуса 2Пі та записуємо множину розв'язків нерівності через проміжки
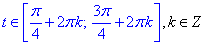
та у вигляді нерівності
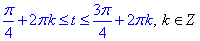
Повертаємося до заміни змінних t=3x та перераховуємо розв'язки
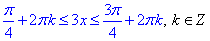
Остаточно, отримаємо нерівність
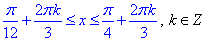
(поділили кожну частину нерівності на 3).
Шукана множина розв'язків прийме вигляд:
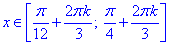
Завдання 19.11 Розв'язати нерівність sin(x/4-1)≤-√2/2.
Розв'язання: Оскільки |-√2/2|≤1, то розв'язок нерівності існує.
Зробимо заміну: t=x/4-1, тоді переходимо до обчислень простішої нерівності
sin(t)≤-√2/2.
Побудуємо одиничне коло, пряму y=-√2/2.
Позначимо точки P[t1] і P[t2] перетину кола й прямої y=-√2/2 та виділимо множину точок, ординати яких не більші -√2/2
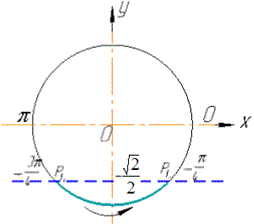
Знайдемо кути перетину прямої з колом t1 і t2:
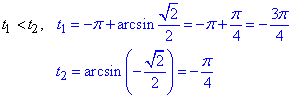
Враховуючи періодичність синуса, записуємо розв'язок через проміжки
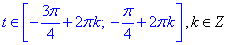
або нерівності
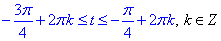
Повернемося до заміни t=x/4-1, та визначимо "ікс"
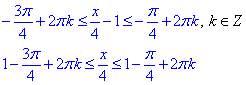
Остаточно, отримаємо
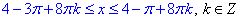
(До всіх частин нерівності додали 1, а потім помножили на 4).
Отже, значення 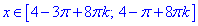
є множиною розв'язків тригонометричної нерівності.
Завдання 19.12 Розв'язати нерівність 2cos(x-5Pi/6)≥-1.
Розв'язання: Задана нерівність еквівалентна нерівності:
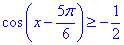
Перевірка ОДЗ показує |-1/2|≤1, що розв'язок нерівності існує.
Виконаємо заміну: t=x-5Pi/6, та переходимо до розгляду простішої нерівності
cos(t) ≥-1/2.
Побудуємо одиничне коло та пряму y=-1/2, позначимо точки P[t1] і P[t2] перетину кола й зазначеної прямої.
Виділимо кольором множину точок, ординати яких не менші -1/2.
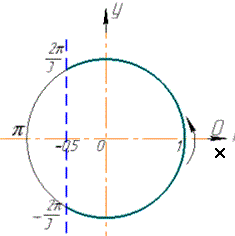
Знайдемо значення точок перетину t1 і t2:
t1<t2,
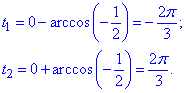
Звідси розв'язок рівний
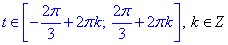
або
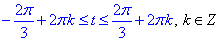
Повернемося до заміни t=x-5Pi/6 та перерахуємо "ікс"
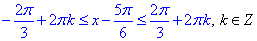
Остаточно, отримаємо
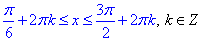
(до кожної частини нерівності додали 5Pi/6).
Записуємо множину розв'язків нерівності у вигляді проміжку
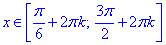
Як Ви могли переконатися у випадку синусів та косинусів зі складним аргументом нерівності не складно обчислювати.
Для тангенса та котангенса схема та ж сама, тільки по другому будуються лінії тангенса та котангенса (див. попередню статтю).
Щоб швидко розв'язувати нерівності вивчіть добре таблицю основних значень тригонометричних функцій.
Це дасть можливість швидко знаходити обернені тригонометричні функції, що фактично і є важливим при розв'язанні нерівностей.
Для прикладу, не знаючи косинус якого кута рівний 1/2 або тангенс якого =√3 важко знайти межі розв'язків нерівностей.
І такі питання в тригонометрії чекатимуть Вашого вирішення на кожному кроці.
Вчіться і нехай все нове легко Вам дається!


