Знайти розв'язок системи лінійних рівнянь третього, четвертого порядку матричним методом

Для розв'язування системи лінійних алгебраїчних рівнянь її записують у матричній формі
A*X=B
де A - матриця, складена з коефіцієнтів при невідомих; X - стовпець невідомих; B - стовпець вільних членів. Тоді, якщо для матриці A існує обернена матриця A^-1 (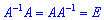 ), то система лінійних рівнянь має єдиний розв'язок і він знаходиться за формулою
X=A^-1*B.
Оскільки перемножити матрицю на вектор стовпець не складає особливих труднощів, то найбільша проблема при обчисленнях – знайти обернену матрицю.
В знаходженні розв'язку за наведеною формулою і полягає суть матричного методу.

Розглянемо декілька прикладів із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".

Приклад 1. Розв'язати систему лінійних алгебраїчних рівнянь.

1) (1. 183)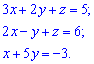

Розв'язок.Запишемо системо трьох лінійних рівнянь у матричній формі

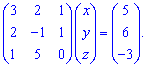
Знайдемо обернену матрицю. Нагадаємо, що її обчислюють за формулою

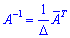
де 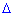- визначник матриці A , а 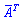- транспонована матриця алгебраїчних доповнень елементів A_ij визначника матриці.
Обчислимо визначник головної матриці


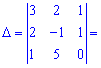
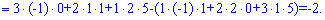
Матрицю алгебраїчних доповнень складається з елементів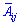 , які обчислюються через мінори за правилом

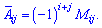
Мінори M_ij - це визначники на порядок менші від визначника 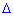, які утворюються викреслюванням в ньому i -го рядка і j - го стовпця. На перший погляд звучить надто запутано, але при обчисленнях все стане зрозуміло і просто.
Знайдемо алгебраїчні доповнення до визначника










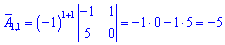
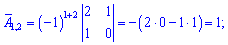
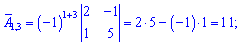
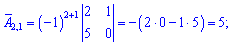
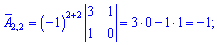
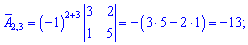
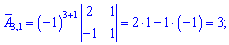
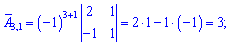
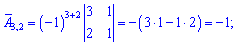
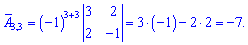
Запишемо знайдену матрицю алгебраїчних доповнень

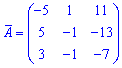
та протранспонуємо її

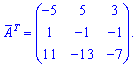
Знаходимо обернену матрицю

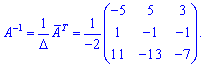
З допомогою оберненої матриці знаходимо розв'язок системи лінійних рівнянь


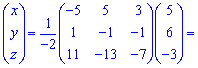
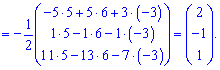
В результаті отримали x₁=2;x₂=-1; x₃=1.

Приклад 2.Знайти розв'язо системи лінійних алгебраїчних рівнянь.
(4. 182)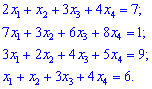

Розв'язок. Cистему лінійних рівнянь четвертого порядку перепишемо в матричній формі

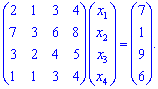
Оскільки всі коефіцієнти ненульві то обчислювати її буде важко. Виконаємо над системою лінійних рівнянь елементарні перетворення, щоб занулити деякі з коефіцієнтів.
Від другого рядка віднімемо перший і останній рядки

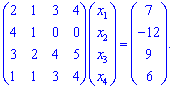
Від третього рядка віднімемо суму першого та четвертого початкової системи

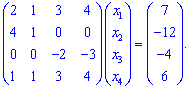
Від четвертого рядка віднімемо перший

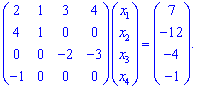
З останнього рядка вже можемо сказати, що перший корінь x₁=1 , але будемо дотримуватись правил, щоб навчитися розв'язувати великі системи рівнянь.
Оскільки матриця стала розрідженою, то обчислення визначника та матриці алгебраїчних доповнень спростяться. Знайдемо визначник матриці, розклавши його за четвертим рядком


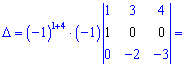
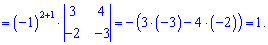
Знайдемо матрицю аглгебраїчних доповнень, розкладаючи шукані детермінанти за рядками і стовпцями, які містять найбільше нулів. Для самоперевірки випишу Вам обчислення тільки першого рядка. Решта спробуйте обчислити самостійно




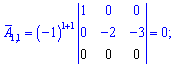
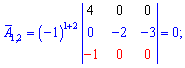
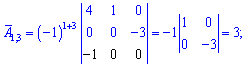
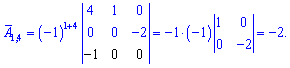
Після знаходження всіх значень отримаємо наступну матрицю доповнень

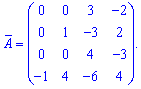
Оскільки визначник рівний одиниці, то обернена матриця з транспонованою матрицею доповнень співпадають

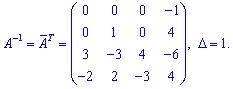
Підставимо у матричний запис та знайдемо розв'язок


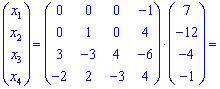
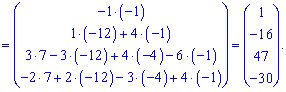
Відповіддю будуть значення x₁=1;x₂=-16; x₃=47; x₄=30.

При обчисленнях систем лінійних алгебраїчних рівнянь третього, четвертого порядку матричним методом доводиться знаходити велику кількість алгебраїчних доповнень, які собою являють визначники другого та третього порядку відповідно. Саме помилки при їх обчисленні найчастіше стають причиною невірного розв'язку. Для уникнення таких ситуацій потрібно добре знати правила знаходження визначників другого, третього порядку, а також правила чергування знаків при мінорах.
Вивчайте їх і отримуйте лише вірні розв'язки. Як бонус - можете завантажити калькулятор систем лінійних рівнянь YukhymCalc.