Розв'язувати системи лінійних алгебраїчних рівнянь другого, третього, зрідка четвертого порядку методом Крамера досить часто доводиться студентам молодших курсів навчання при вивченні основ лінійної алгебри. Для більшості студентів стаціонарної форми навчання такі завдання не є складними, однак хто вибрав заочне навчання чи дистанційне, або пропустив з певних причин практичні заняття обчислення виглядають незрозумілими і важкими. Щоб виправити таку ситуацію в даній статті будуть наведені найбільш поширені приклади даної теми та схема їх розв'язання. Якщо Ви добре зрозумієте принцип їх розв'язування, то на практиці у Вас не буде труднощів з подібними завданнями.
Для початку виберемо завдання із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Розв'язати систему лінійних алгебраїчних рівнянь.
1) (1. 153)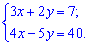 
Розв'язок. У випадку двох рівнянь розв'язок можна отримати простішим способом. Виразимо з другого рівняння x
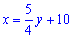
та підставимо у перше
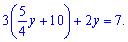
Розкривши дужки, згрупуємо подібні доданки
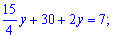
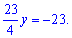
Звідси отримаємо розв'язок y=-4.
Змінну x знайдемо підстановкою y у будь-яке із рівнянь
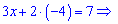
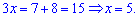
Таким чином розв'язком системи двох рівнянь будуть значення x=3; y=-4.
Оскільки мета статті навчити студентів розв'язувати методом Крамера, то розв'яжемо даний приклад і ним.
Для цього випишемо систему лінійних рівнянь у вигляді
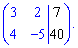
Знайдемо детермінант основної частини
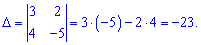
Для обчислення допоміжних визначників ставимо стовпець вільних членів на місце першого рядка для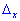 
та на місце другого для 
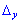. В результаті отримаємо
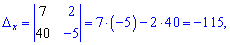
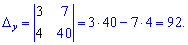
Підставимо знайдені значення в формули Крамера
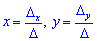
та знайдемо невідомі
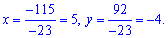
З розглянутого прикладу видно, що обчислення при двох рівняннях з двома невідомими досить прості.
Далі будуть наведені обчислення для систем іх трьох рівнянь.
2) (1. 165)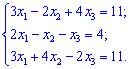
Розв'язок. Запишемо систему трьох рівнянь у зручному для розв'язування вигляді
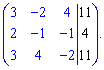
Знайдемо детермінант системи за правилом трикутників
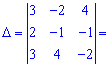
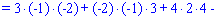
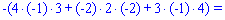
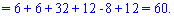
Для знаходження додаткових визначників підставляємо стовпець вільних членів на місце першого, другого та третього стовпців. В результаті прийдемо до детермінантів
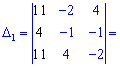
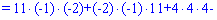
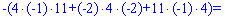
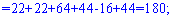
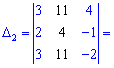
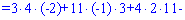
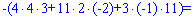
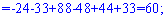
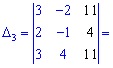
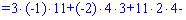
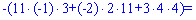
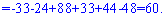
Обчислюємо невідомі за формулами Крамера
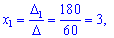
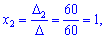
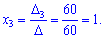
Для даної системи рівнянь знаходження розв'язку теж не надто складно, хоча в порівнянні з системою двох рівнянь обчислень помітно прибавилося.
3) (1. 174)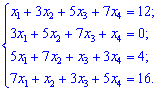 
Розв'язок. Перетворимо систему рівнянь четвертого порядку до вигляду
Знаходимо головний визначник системи. При обчисленні детермінантів четвертого порядку їх вартує розкладати за рядками чи стовпцями в яких найбільше нулів. Оскільки, в даному випадку нулів головний визначник немає, то розкладемо його за першим рядком
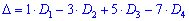
та знайдемо відповідні детермінати третього порядку
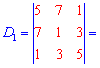
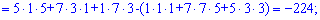
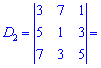
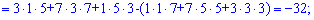
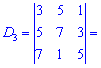
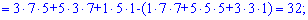
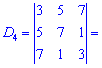
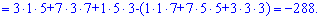
Підставимо знайдені значення у визначник
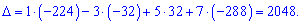
За такою ж схемою обчислюємо допоміжні визначники, нагадаю лише, що вони утворюються заміною стовпця у головному визначнику на стовпець вільних членів (позначений чорним кольором). Я не проводитиму детальних розписувань всіх розрахунів, проте Ви можете перевірити, що детермінанти приймуть значення
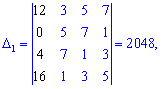
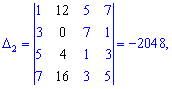
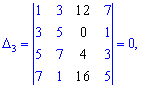
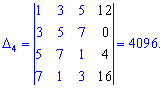
Підставивши в формули Крамера, після обчислень отримаємо x1=1; x2=-1; x3=0; x4=2
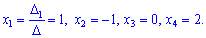
На цьому завдання розв'язано. Системи чотирьох лінійних рівнянь найбільш трудомісткі в обчисленнях, для визначення їх розв'язку потрібно обчислювати 5*4=20 визначників третього порядку, в той час як системи трьох рівнянь лише 4. Будьте уважні при обчисленнях, адже найменша помилка може мати наслідком неправильний результат.
