Функціональним рядом називається ряд складений з членів, які є функціями від аргументу x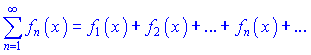 При кожному конкретному значенні x із області визначення
При кожному конкретному значенні x із області визначення ![]() функціональний ряд перетворюється на числовий.
функціональний ряд перетворюється на числовий.
Якщо для ![]() числовий ряд
числовий ряд 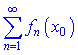 збігається, то кажуть, що функціональний ряд збігається в точці x0 , а саму точку називають точкою збіжності.
збігається, то кажуть, що функціональний ряд збігається в точці x0 , а саму точку називають точкою збіжності.
Множина всіх значень змінної x, при яких функціональний ряд збігається називається областю збіжності ряду. На практиці розглядають ряди, областями збіжності яких є різні інтервали осі Ox.
В точках із області збіжності ряду існують значення суми ряду S, а також можна встановити залежність між точками збіжності та значеннями сум. Таким чином, сума функціонального ряду є функцією f(x), область визначення якої ідентична області збіжності функціонального ряду. При цьому, кажуть, що функціональний ряд збіжний до функції f(x) , або функція розкладається в ряд
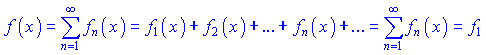
в його області збіжності.
Функціональний ряд вигляду
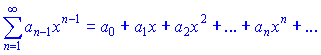
де a0, a1, a2,... сталі коефіцієнти, називають степеневим рядом.
Часто розглядають степеневий ряд більш загального вигляду
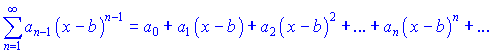
де b=const.
ОЗНАКА ВЕЙЄРШТРАССА
Функціональний ряд вигляду
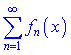
абсолютно і рівномірно збіжний на проміжку (a; b), якщо існує знакододатний збіжний числовий ряд ![]() такий, що для всіх змінних з цього інтервалу
такий, що для всіх змінних з цього інтервалу ![]() виконується умова
виконується умова
![]()
ОЗНАКА ЗБІЖНОСТІ СТЕПЕНЕВОГО РЯДУ
Теорема Абеля. Якщо степеневий ряд збігається в точці x=x0<>0 , то він збігається абсолютно в інтервалі
![]()
Якщо степеневий ряд розбіжний в точці ![]() , то він буде розбіжний для всіх змінних x , що задовольняють умову
, то він буде розбіжний для всіх змінних x , що задовольняють умову
![]()
число R=|x0| називають радіусом збіжності степеневого ряду,
а проміжок (-R; R)- інтервалом збіжності (областю збіжності).Якщо всі коефіцієнти ряду ненульові, то радіус збіжності рівний наступній границі
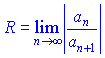
при умові, що вона існує (скінченна чи нескінченна).
Для рядів вигляду
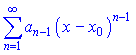
радіус збіжності визначається за формулою R , проте інтервал збіжності з нерівності
![]()
Теорема не дає відповіді про збіжність на кінцях інтервалу, тому їх слід перевіряти окремо за відомими ознаками збіжності.
Розглянемо приклади на знаходження області збіжності степеневого ряду.
Дослідження збіжності степеневих рядів
Приклад 1. Знайти область збіжності функціонального ряду
1) (9.181) 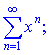
Розв'язок. Даний ряд знакододатний. Для того, щоб вионувалася необхідна умова збіжності потрібно, щоб ряд був монотонно спадним
![]()
Поділивши на xn, отримаємо, що це виконується за умови x<1.
Отже, областю збіжності даного ряду є інтервал (-1; 1).
2) (9.182) 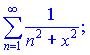
Розв'язок.За ознакою Вейєрштраса, даний ряд збіжний для всіх змінних![]() , оскільки кожен член ряду
, оскільки кожен член ряду
![]()
менший відповідного члена ряду геометричної прогресії 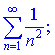
який є збіжним. Таким чином, отримуємо безмежну область збіжності -![]()
3) (9.183) 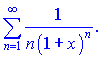
Розв'язок. Даний ряд від гармонічного відрізняється множником в знаменнику (1+x)n.
Якщо цей множник по модулю буде більший одиниці, то ряд буде збіжним. З цієї умови отримаємо нерівність
![]()
Для даного ряду отримали два проміжки ![]() на яких ряд буде збіжний.
на яких ряд буде збіжний.
Приклад 2. Знайти область збіжності степеневих рядів
1) (9.211) 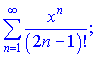
Розв'язок. Знайдемо радіус збіжності ряду
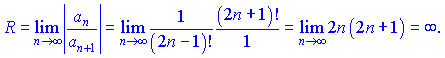
Будьте уважними при спрощенні факторіалів.
Радіусом збіжності буде інтервал ![]()
2) (9.212) 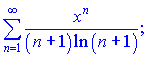
Розв'язок. Обчислимо границю відношення членів ряду
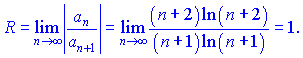
Вона рівна одиниці, отже інтервал збіжності рівний (-1; 1).
Дослідимо поведінку наступних рядів
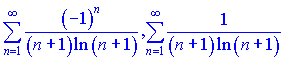
щоб дати відповідь на питання про збіжність ряду на краях знайденого інтервалу.
Перший ряд – знакопочерговий. За ознакою Лейбніца
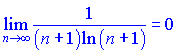
ряд збігається.
Другий ряд перевіримо за інтегральною ознакою Коші
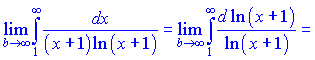
![]()
Даний ряд розбіжний, границя рівна безмежності.
Таким чином інтервалом збіжності ряду буде проміжок [-1; 1).
3) (9.213)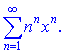
Розв'язок. Знайдемо радіус збіжності R
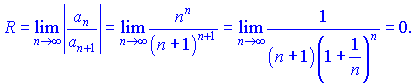
Радіус збіжності ряду рівний нулю, а це значить, що ряд збіжний лише в точці x=0.
Застосовуйте ознаку Веєрштраса, наведені формули для встановлення збіжності функціональних рядів та обчислення радіусу збіжності.


