Всі хто шукає готові відповіді на лінійні диференціальні рівняння прийшли за правильною адресою. В нас Ви зможете не тільки отримати швидку відповідь, а й навчитися методики розв'язання рівнянь. Чи складна схема Бернуллі для лінійних рівнянь залежить від Вашого рівня підготовки. Розберіть уважно наведені відповіді та зробіть висновки, що і як Вам потрібно поглиблено вивчити.
Лінійним диференціальним рівнянням першого порядку називається рівняння виду y'+p(x)*y=g(x), де p(x) та g(x) – неперервні на певному проміжку функції.
Алгоритм методу Бернуллі
1.Розв'язок лінійного диференціального рівняння необхідно подати у вигляді добутку двох невідомих функцій y=u*v від аргумента u=u(x),v=v(x).
Одну з цих функцій можна вибрати довільно, а друга визначається з даного рівняння.
2. За правилом похідна добутку рівна y=u*v,то y'=u'*v+u*v'.
3. Підставимо запис функції y=u*v та похідної y'=u'*v+u*v' у рівняння y'+p(x)*y=g(x) і одержимо u'v+uv'+p(x)*u*v= g(x).
Згрупуємо другий і третій доданки, винісши спільний множник (u) за дужки і прийдемо до диф. рівняння u'v+u(v'+p(x)*v)=g(x).
4. Спершу визначаємо частинний розв'язок v=v(x), для цього розв'язуємо диф. рівняння v'+p(x)*v=0 і за довільну сталу інтегрування беремо нуль (С=0). Дане рівняння є диференціальним рівнянням з відокремлюваними змінними.
5. Далі підставимо знайдену функцію v=v(x) в вихідне диф. рівняння u'*v+u*v'+p(x)*u*v= g(x), яке при цьому спроститься до u'*v+u*0=g(x), тобто до диференціального рівняння з відокремлюваними змінними u'*v(х)=g(x) відносно u(x).
З цього рівняння знаходимо u=u(x)+С.
6. Маючи u=u(x) та v=v(x), знаходимо загальний розв'язок через добуток y=u*v=( u(x)+С)* v(x).
7. Якщо задана задача Коші, то з додаткової умови на розв'язок y(x0)=y0 довизначаємо константу С.
Приклад 1. (5.13) Знайти розв'язок задачі Коші:
Розв'язання: Маємо неоднорідне диференціальне рівняння першого порядку.
Запишемо його у правильному вигляді, для цього перенесемо y в праву сторону функцію
Далі за схемою Бернуллі робимо заміну змінних
y=u*v,
y'=u'*v+u*v', де u=u(x) і v=v(x).
Враховуючи, що множники в лівій частині рівні
і y2=u2v2
отримаємо таке рівняння
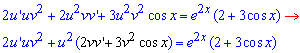
Згідно алгоритму Бернуллі рівняння розділимо на 2, для цього дужку зліва (виділена чорним) прирівняємо до нуля
Зводимо до диференціального рівняння з відокремленими змінними
та розв'язуємо інтегруванням
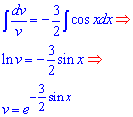
В результаті отримали експоненту з від'ємним показником синуса.
При цьому вихідне диференціальне рівняння достатньо спроститься для відшукання другої, невідомої поки що функції
Перенесемо експоненту з від'ємним показником в праву сторону
та зведемо до диференціального рівняння з відокремленими змінними
Інтегруванням рівняння в диференціалах
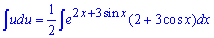
обчислюємо розв'язок диференціального рівняння
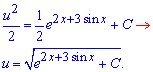
Як описано на початку, загальний розв'язок диференціального рівняння рівний добутку функцій
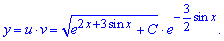
Але це ще не кінцева відповідь до завдання.
Знайдемо частковий розв'язок диференціального рівняння (задача Коші), для цього знаходимо сталу з початкової умови на функцію
Стала рівна нулю. Це дозволяє спростити формулу розв'язку диф. рівняння, хоча мало хто з Вас побачить дану підказку
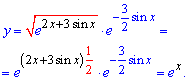
Ми знайшли частковий розв'язок диференціального рівняння і він рівний експоненті в степені "ікс" y=ex.
Приклад 2. (5.19) Знайти розв'язок задачі Коші:
Розв'язання: Задано неоднорідне диференціальне рівняння першого порядку, яке можна подати у вигляді
Виконуємо заміну змінних у рівнянні:
де "у" і "в" приймають функційні залежності
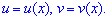
Знаходимо вирази, що фігурують в рівнянні
та підставимо їх у вихідне диференціальне рівняння
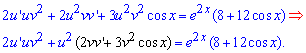
Далі схема обчислень полягає в розділенні змінних.
За алгоритмом Бернуллі вираз, що містить "v" прирівняємо до нуля
Записуємо рівняння через диференціали
і перетворюємо до диф. рівняння з відокремленими змінними
При інтегруванні правої та лівої частин
отримаємо логарифм та синус.
Далі експонуємо праву та ліву частину та отримаємо одну з невідомих функцій
Початкове диференціальне рівняння при цьому спроститься до вигляду
Експоненту у відємному показнику переносимо вправо від знаку рівності
Далі розписуємо рівняння через диференціали (/2)
та зводимо до рівняння з відокремленими змінними
Інтеграл в правій частині виглядає важким для числення, але якщо внести дужку під диференціал, то отримаємо показник експоненти
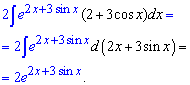
Остаточно після інтегрування отримаємо
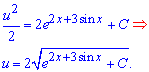
Загальний інтеграл диференціального рівняння записуємо через добуток функцій
Щоб знайти частковий розв'язок диференціального рівняння (задача Коші) використаємо початкову умову
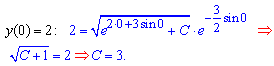
З неї встановимо сталу та підставимо у рівняння часткового розв'язку диференціального рівняння
На цьому і побудований алгоритм Бернуллі обчислень диференціальних рівнянь такого типу.
Приклад 3. Знайти частинний розв'язок лінійного диференціального рівняння першого порядку.
y'-y/x=x^3+2, y(1)=1/3.
Обчислення: Розпишемо рівняння у диференціалах, розділимо змінні та проінтегруємо отримані вирази
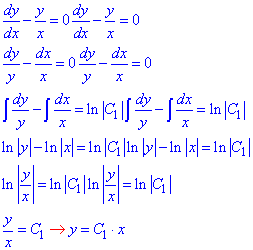
y=C1•x - загальний розв'язок рівняння (*).
Щоб визначити сталу подамо її як функцію від "ікс"
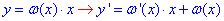
тоді ДР перетвориться до наступного
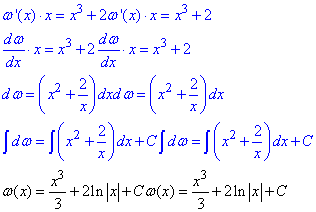
Останній запис і є шуканим частковим розв'язком ДР.
Підставимо у формулу (*)
y=x^4/3+2x·ln|x|+xC - повний розв'язок рівняння.
Розв'яжемо задачу Коші, для цього підставимо початкову умову y(1)=0,5 у повний розв'язок ДР:
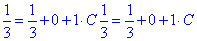
звідси C=0. Отже,
y=x^4/3+2x·ln|x| - частинний розв'язок рівняння.
На сайті достатньо матеріалів, щоб тема за темою вивчити усі розділи диференціальних рівнянь, що вивчають у ВУЗах.
В цьому уроці не вмістилися усі приклади, що ми підготували для Вас на метод Бернуллі, тому перегляньте наступні 2, де в стислій формі продовжуємо навчати Вас розв'язувати різні диференціальні рівняння.
