Готові відповіді до контрольної роботи з диференціальних рівнянь стануть в нагоді бігатьом студентам. Дочитайте уважно пояснення до розв'язків і подібні зможете розв'язати самостійно. Тут Вам однорідні та неоднорідні диференціальні рівняння, завдання на складання характеристичного рівняння, системи диференціаьних рівнянь. Контрольна з диференціальних рівнянь містить 10 різнотипних завдань і охоплює більшість тем предмету.
Приклад 1. Знайти частинний розв'язок рівняння
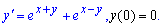
Обчислення: На вигляд рівняння складне, але розділивши змінні можна звести до рівняння з відокремленими змінними
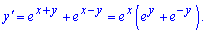
Записуємо рівняння в диференціалах та відокремлюємо змінні
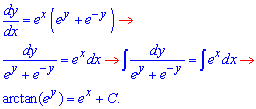
Це є загальний інтеграл диф. рівняння, записаний в неявному вигляді. Виразимо із нього саму функцію y
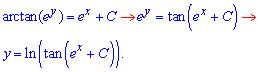
Лишилося задовільнити умову Коші
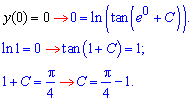
Таким чином, частинний розв'язок ДР рівний
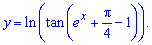
Приклад 2. Розв'язати диференціальне рівняння (ДР)
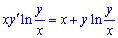
Обчислення: Розділимо рівняння на x
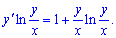
Бачимо, що всюди маємо множники виду y/x
Введемо заміну змінних
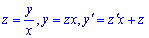(1)
та підставимо у рівняння
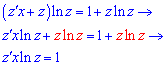
Два подібні доданки спростяться (позначені червоним). Далі розписуємо рівняння в диференціалах та відокремлюємо змінні
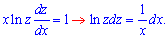
Інтегруємо обидві частини ДР, до першого застосовуємо інтегрування частинами udv, другий інтеграл дасть логарифм.
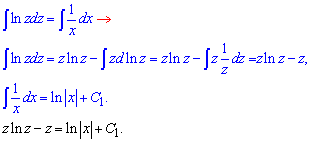(2)
Повертаємося до заміни змінних та записуємо
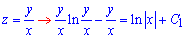- загальний інтеграл диференціального рівняння.
Приклад 3. Розв'язати диференціальне рівняння
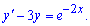
Обчислення: Маємо неоднорідне диференціальне рівняння першого порядку. Розв'язок шукаємо через суму однорідного та частковий розв'язок неоднорідного ДР. Для однорідного ДР
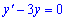
корені шукаємо у вигляді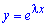 
Складаємо характеристичне рівняння
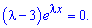
Так як експонента завжди більша нуля, то на неї ділимо, в результаті отримаємо рівняння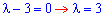 
з якого записуємо розв'язок однорідного диференціального рівняння
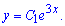
Розв'язок неоднорідного ДР шукаємо у вигляді правої сторони (експоненти)
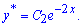
Підставимо у неоднорідне диференціальне рівняння
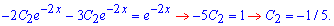
Розв'язок неоднорідного ДР наступний
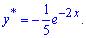
Загальний розв'язок ДР записуємо через суму знайдених
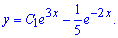
Приклад 4. Розв'язати диференціальне рівняння
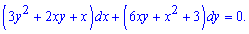
Обчислення: Маємо рівняння схоже на ДР в повних диференціалах. Перевіримо умову на часткові похідні
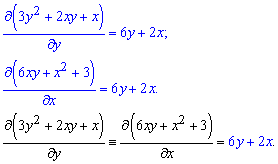
Умова рівності часткових похідних виконується, отже маємо ДР в повних диференціалах. Розв'яжемо його за першою частиною
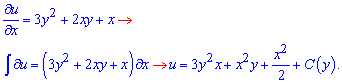
Щоб до визначити сталу знаходимо часткову похідну по y і прирівнюємо до другого доданку
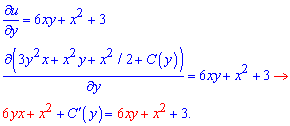
Подібні доданки спрощуємо і приходимо до такого ДР на сталу
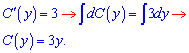
Підставляємо сталу в загальний розв'язок диференціального рівняння
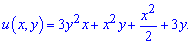
на цьому приклад розв'язано.
Приклад 5. Зінтегрувати диференціальне рівняння (ДР)
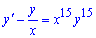
Обчислення: Розв'яжемо ліву – однорідну частину диференціального ріняння
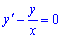
Запишемо рівняння в диференціалах та зведемо до ДР з відокремленими змінними
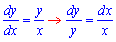
Проінтегруємо обидві частини
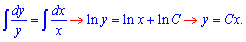
Щоб задовільнити праву (неоднорідну) частину рівняння припустимо, що стала є функцією від змінної C=C(x) та підставимо у початкове ДР. У результаті отримаємо
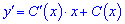- похідна функції
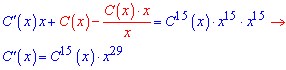- диференціальне рівняння відносно сталої.
Розписуємо рівняння в диференціалах та інтегруємо його
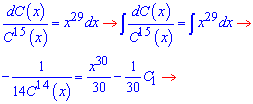
Тут для зручності при C1 ввели такий же множник як і при змінній. Далі виражаємо саму сталу
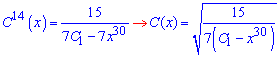
Залишилося підставити її в кінцеву формулу розв'язку ДР
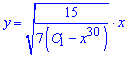
Приклад 6. Розв'язати диференціальне рівняння
а)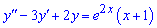 
Обчислення: Складемо характеристичне рівняння для відповідного однорідного ДР
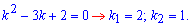
Оскільки корені характеристичного рівняння різні дійсні числа, то розв'язком коренем однорідного рівняння буде функція
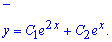
Частковий розв'язок неоднорідного ДР шукаємо у вигляді правої частини з невідомими коефіцієнтами, помноженої на x, оскільки степінь експоненти співпадає з коренем характеристичного рівняння
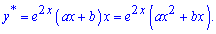
Знаходимо першу і другу похідні
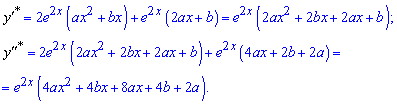
Знайдені значення підставляємо в ДР, розділивши останнє на exp(2x). В результаті отримаємо
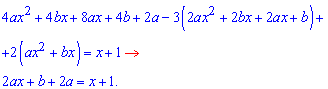
При квадратах змінної доданки скоротяться, решта після групування та при рівняння до правої частини дадуть таку систему рівнянь для визначення констант a,b
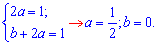
Отже частковий розв'язок відповідного ДР має вигляд
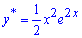
а загальний розв'язок ДР наступний
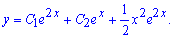
б)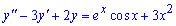 
Обчислення: Характеристичне рівняння буде ідентичним як у пункті а) цього прикладу, тому корінь однорідного рівняння такий самий
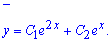
Далі, оскільки права частина містить як експоненту так і функцію від змінної, то розіб'ємо частковий розв'язок ДР на 2.
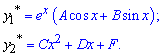
Знайдемо похідні від першої ф-ї
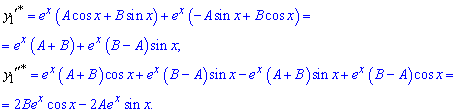
та підставимо у ДР, поділивши на експоненту обидві частини рівняння
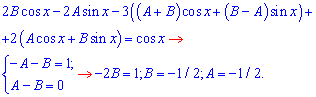
Перший частковий розв'язок ДР рівний
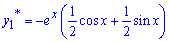
За такою ж схемою знаходимо 2 частковий розв'язок
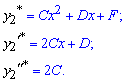
При підстановці у рівняння отримаємо
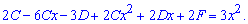
Прирівнюємо множники при однакових степенях змінної та складаємо систему рівнянь
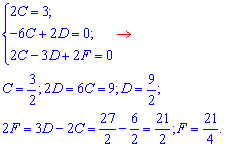
Записуємо 2 частковий розв'язок рівняння
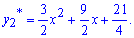
Загальний розв'язок ДР рівний сумі 3 знайдених
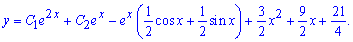
В подібних завданнях на ДР також старайтеся розбити частковий розв'язок на декілька, це спрощує пошук констант та самі обчислення.
в)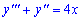 
Обчислення: Відповідне однорідне ДР розв'яжемо методом пониження степеня (введення параметра). Позначимо другу похідну через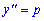 
, тоді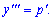 
Однорідне ДР при цьому набуде вигляду
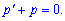
Записуємо в диференціалах, розділяємо змінні та інтегруємо
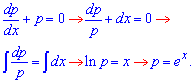
Згадуємо чому рівний параметр і відновлюємо функцію інтегруванням другої та першої похідних
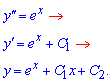
Враховуючи вигляд правої сторони рівняння, а також відсутність функції та її першої похідної, частковий р-зок неоднорідного ДР шукаємо у вигляді
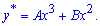
Обчислюємо 2 та 3 похідні
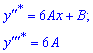
та підставляємо у рівняння
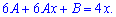
Прирівнюємо однакові коефіцієнти
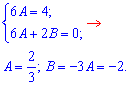
Частковий р-зок неоднорідного ДР має вигляд
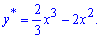
Щоб отримати загальний р-зок ДР до знайденого часткового додаємо корінь однорідного ДР
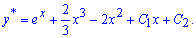
Останні два завдання контрольної на системи диференціальних рівнянь будуть розібрані в наступній статті.
В подібних ДР розбираємося добре, тому сміло можете звертатися за допомогою та консультацією.
