Готові відповіді з диференціальних рівнянь

В попередній частині контрольної роботи з диференціальних рівнянь проаналізовано відповіді до рівнянь з відокремленими змінними, першого порядку, рівняння Бернулі та в повних диференціалах. Хто їх не читав рекомундуємо повернутися, та переглянути відповіді на диференціальні рівняння. Тут будуть проаналізовані готові відповіді з ДР, які не увійшли в попередню статтю.

Приклад 7. (7.22) Знайти інтегруючий множник та розв'язати задачу Коші

Розв'язання: Запишемо ДР у диференціалах

Перевіримо чи виконується умова на повний диференціал. Позначимо

та обчислимо часткові похідні

З їх значень робимо висновок, що ліва частина рівняння не є повним диференціалом

Таких завдань не багато і рівняння такого типу називають звідними до рівнянь в повних диференціалах. Для подальших обчислень перевіримо чи допускає ДР інтегруючий множник ?

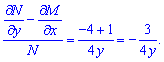
Тут він залежний від функції y. Вам можуть зустрітися завдання, де інтегруючий множник залежить від аргументу, або від добутку y*x. Таким чином встановили, що задане ДР допускає інтегруючий множник, його значення знаходимо за формулою

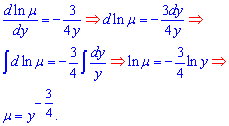
Після множення всіх доданків ДР на "м'ю" отримаємо рівняння

в повних диференціалах
().
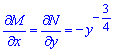Схему обчислення ДР в повних диференціалах Ви вже знаєте, тому для простоти обчислень вибираємо другий множник та після розділення змінних виконуємо інтегрування.

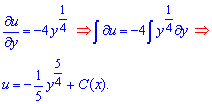
Знаходимо похідну функції за аргументом та довизначаємо сталу

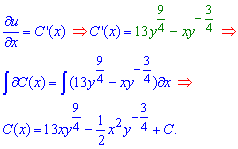
Маємо все для того, щоб записати загальний інтеграл диференціального рівняння

Розв'яжемо задачу Коші.
Записуємо початкову умову для функції

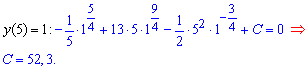
З рівняння знаходимо сталу та підставляємо в частинний інтеграл ДР

На цьому завдання розв'язано.
Добре перегляньте та випишіть в чорновик схему відшукання інтегруючого множника.
Хто вчиться на математичному факультеті гарантовано буде розбирати подібне диференціальне рівняння.

Приклад 8. (8.10) Знайти загальний розв'язок диференціального рівняння:

Розв'язання: Маємо неоднорідне диференціальне рівняння другого порядку.
Загальний інтеграл шукаємо у вигляді суми двох функцій

Спершу розв'язуємо однорідне диференціальне рівняння:

Для пониження степеня рівняння використовуємо метод параметра

Рівняння перетвориться до однорідного ДР першого порядку

Зводимо його до ДР з відокремленими змінними та інтегруємо

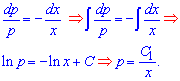
Далі повертаємося до заміни та знаходимо розв'язок однорідного рівняння

Обидві сталі набувають довільних значень.
Тепер спробуємо проаналізувати просту на вигляд неоднорідну частину рівняння. Щоб друга похідна помножена на "ікс" в 4 степені дорівнювала сталій, функцію підбираємо інтегруванням. Знаки і числа нас не цікавлять, тільки функціональна складова

Звідси частковий розв'язок рівняння подамо у вигляді

Щоб знайти коефіцієнт A обчислюємо дві похідні

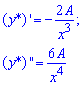
та підставимо в початкове ДР
6A-2A=1; A=1/4.
Можемо записати явний вигляд другої функції

Додаючи до неї однорідний розв'язок отримаємо загальний розв'язок диференціального рівняння:
,
де C₁, C₂ - довільні константи.

Приклад 9. (9.11) Знайти загальний розв'язок диференціального рівняння:

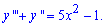
Розв'язання: Маємо неоднорідне диференціальне рівняння третього порядку, тільки в ньому на відміну від попереднього завдання, однорідна частина не містить множників залежних від "ікс".
В такого сорту ДР розв'язок однорідного рівняння шукаємо у вигляді комбінації функцій y=e^k*x.
Підставивши у відповідне однорідне рівняння і спростивши на експоненту отримаємо характеристичне рівняння
k³+k²=0
з якого знайдемо корені
k₁=k₂=0, k₃=-1.
Оскільки обидва корені характеристичного рівняння є дійсні числа, причому - однакові, то розв'язок однорідного рівняння рівний

Далі проаналізуємо неоднорідну складову рівняння – вона виражається квадратичною функцією, тому частковий розв'язок шукаємо у вигляді

Знайдемо 3 коефіцієнти, для цього обчислимо похідні

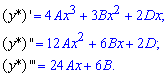
та підставимо у вихідне ДР

Прирівнюючи коефіцієнти при однакових степенях, складаємо систему рівнянь з якої визначаємо сталі

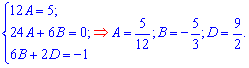
При підставці в формулу часткового розв'язку отримаємо

Додавши до нього інтеграл однорідного рівняння будемо мати загальний розв'язок ДР

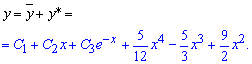
Сталі C₁, C₂, C₃ приймають довільне значення.
Якщо б завдання містило умову Коші то з попередніх завдань Ви могли бачити, як легко можна знайти сталі та забезпечити виконання умови Коші. 

Приклад 10. (10.4) Знайти загальний розв'язок диференціального рівняння:

Розв'язання: Задане неоднорідне диференціальне рівняння третього порядку, однорідна частина якого містить 1-3 похідні функції і не містить аргументів. В такому випадку інтеграл однорідного рівняння шукаємо через експоненту.
Складемо характеристичне рівняння для однорідного ДР та визначимо розв'язки
k³-2k²+k=0 -> k₁=0, k₂=k₃=1.
Отримали дійсні корені характеристичного рівняння, два з яких рівні між собою.
В таких випадках розв'язок однорідного рівняння записуємо формулою

Неоднорідна частина заданого рівняння (2x+5)e^2x має вигляд полінома P(x)e^2x, причому степінь експоненти не співпадає з коренями характеристичного рівняння. Це дозволяє шукати частковий розв'язок у вигляді подібному до правої сторони рівняння

Для визначення сталих A, B необхідно взяти похідні функції

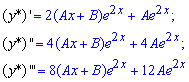
підставити в задане диференціальне рівняння, далі прирівняємо коефіцієнти при однакових степенях "ікс":

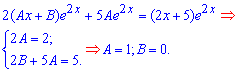
Отримаємо частковий розв'язок ДР

Загальний розв'язок диференціального рівняння знаходимо сумуванням

Тільки що Ви навчилися розв'язувати ще один тип диференціальних рівнянь.
Доречі зауважте, що для обчислень в цьому та попередньому завданні ми не застосовували інтегрування.

Приклад 11. (26) Знайти загальний розв'язок диференціального рівняння:

Розв'язання: Цього разу неоднорідна частина диференціального рівняння другого порядку містить тригонометричні функції.
Розв'язок однорідного ДР шукаємо через експоненти y=exp(k*x),
При підстановці функції в ДР та діленні на експоненту отримаємо залежність з якої знаходимо комплексно спряжені корені характеристичного рівняння, причому лише уявні частини

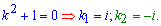
Повертаючись до експонент отримаємо наступне значення кореня однорідного рівняння

Обов'язково запам'ятайте цей перехід. Інші варіанти таких неоднорідних рівнянь Ви можете розібрати з уроку про комплексні корені характеристичного рівняння.
Частковий розв'язок запишемо у вигляді неоднорідної частини рівняння

Далі обчислюємо сталі A,B за відомою всім схемою – знаходимо похідні функції та вносимо їх у рівняння

В результаті прийдемо до тригонометричної залежності, з якої з коефіцієнтів при синусу та косинусу складаємо систему рівнянь, далі визначаємо сталі

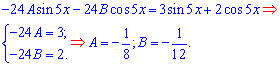
Таким чином ми можемо записати формулу часткового розв'язку ДР

Підтавляємо знайдені "ігрики" в загальний розв'язок диференціального рівняння:

Умови Коші в завданні не задано, тому сталі залишаємо як є.

Приклад 12. (22) Знайти загальний розв'язок диференціального рівняння:

Розв'язання: Перед Вами одне з складних неоднорідних диференціальних рівнянь.
Ліва - однорідна частина, що містить похідні не важка. Проблеми в студентів виникають при відшуканні часткового розв'язку неоднорідного рівняння.
Отож підставимо експоненту в однорідне рівняння та з характеристичного рівняння обчислимо корені

Отримали комплексно спряжені уявні числа. Такі варіанти в попередніх завданнях розглядалися і у відповідь можемо записати функцію

Дальше бачимо, що аргументи синуса і косинуса в правій частині ДР співпадають з аргументами розв'язку однорідного ДР (характеристичними числами). В таких випадках частковий розв'язок шукаємо у вигляді правої частини, тільки перед синусом та косинусом додатково має бути множник "ікс".

Якщо неоднорідна частина не співпадає з однорідним розв'язком, то функцію записуємо без множника.
Далі повторюємо схему попередніх завдань, а саме - знаходимо похідні

Отримані залежності підставимо в початкове ДР, в результаті цього отримаємо рівняння, з якого виписуємо множники при sin(9x), cos(9x), e^9x

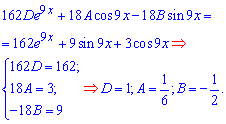
Система рівнянь настільки проста, що для визначення сталих ні методу Гауса, ні Крамера застосовувати не потрібно.
Кожне з рівнянь системи містить тільки одну сталу.
Три знайдені сталі (константи) підставимо в частковий розв'язок ДР

Додаємо дві функції разом та записуємо загальний розв'язок диференціального рівняння

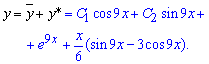
Усі завдання вирішені, методика обчислень диференціальних рівнянь детально розжована, подібні завдання можете переглянути в тій же категорії статей.
На контрольній, модулях чи екзаменах Вам обов'язково доведеться вирішувати завдання на ДР подібного типу. Тому наведені відповіді до контрольної роботи з диференціальних рівнянь детально перегляньте, основні схеми та прийоми занотуйте та використовуйте на практиці.
Якщо бачите, що навчитися до такого рівня Вам не під силу, то завжди можете звернутися за допомогою.
Ми допомогли багатьом студентам успішно скласти іспити, зможемо виручити і Вас!